Convexité et inégalité de Jensen
Fonctions convexes
On peut maintenant définir ce qu'est une fonction convexe.
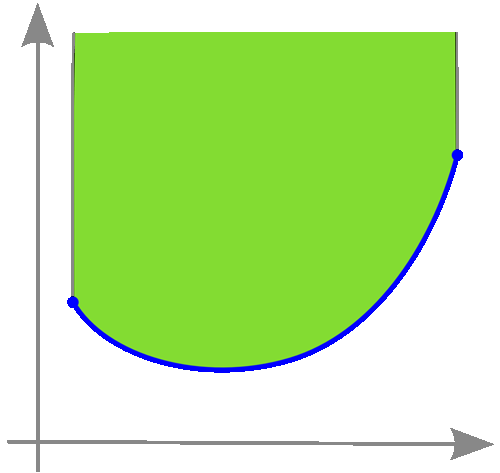
Exemple de fonction convexe.
Une manière équivalente de définir la convexité est de dire qu'une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ est convexe sur $I$ si pour tous $a,b \in I$ et tout $\lambda \in [0,1]$, on a
$$f(\lambda a + (1-\lambda) b) \leq \lambda f(a) + (1-\lambda) f(b).$$ On remarque en effet que
$$(\lambda a + (1-\lambda) b, \lambda f(a) + (1-\lambda) f(b)) = \lambda (a, f(a)) + (1-\lambda) (b, f(b))$$ est le point du segment de droite reliant $(a,f(a))$ à $(b,f(b))$ d'abscisse $\lambda a + (1-\lambda) b$. Par ailleurs, $f(\lambda a + (1-\lambda) b)$ est la valeur de la fonction $f$ en ce même point. L'inégalité signifie donc que les segments de droite reliant deux points du graphe de $f$ ont tous leurs points au dessus du graphe.
Une fonction est par contre dite concave si l'ensemble des points en dessous du graphe de $f$ forme un ensemble convexe. Attention : cela ne revient pas à demander que l'ensemble des points au dessus du graphe est concave ! Contrairement aux ensembles qui sont soit convexes, soit concaves, il existe donc des fonctions qui ne sont ni convexes ni concaves.
Lors d'une compétition, il n'est cependant pas réellement nécessaire de prouver qu'une fonction basique est concave ou convexe. En effet, on sait qu'il suffit de dériver deux fois la fonction pour démontrer qu'elle est convexe ou concave, ce qui se fait de manière automatique.
En pratique, on dessine le graphe de la fonction pour voir si elle est convexe ou concave en regardant l'ensemble délimité par le graphe. Il n'est donc pas important de connaître les dérivées : il faut juste retenir que la convexité ou concavité d'une fonction peut être vérifiée rigoureusement à l'aide des dérivées.
Si la fonction qui nous intéresse est par contre plus exotique comme par exemple $\displaystyle f : x \mapsto \frac{x^4}{24} + \frac{p^2x^2}{4} - \frac{px^3}{6}$ (pour un paramètre $p$), il faudra tout de même calculer $\displaystyle f''(x) = \frac{x^2 + p^2}{2} - xp$ et montrer que $f''$ est positif pour démontrer que $f$ est convexe.
Il est cependant rare d'être dans un tel cas et une vérification graphique suffit généralement amplement. La connaissance des dérivées n'est donc pas du tout nécessaire pour continuer à explorer les inégalités !
Remarque : Les fonctions $f$ vérifiant $f''(x) = 0$ $\forall x \in I$ sont convexes et concaves. Il s'agit en fait des fonctions affines $f(x) = ax + b$ dont le graphe est une droite.
Exemples :
Définition
Une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ (où $I$ est un intervalle) est convexe sur $I$ si $\{(x,y) \in I \times \mathbb{R} \ | \ y \geq f(x)\}$ est convexe, c'est-à-dire si l'ensemble des points au dessus du graphe de $f$ forme un ensemble convexe.

Exemple de fonction convexe.
Une manière équivalente de définir la convexité est de dire qu'une fonction $f:I\subseteq\mathbb{R}\to\mathbb{R}$ est convexe sur $I$ si pour tous $a,b \in I$ et tout $\lambda \in [0,1]$, on a
$$f(\lambda a + (1-\lambda) b) \leq \lambda f(a) + (1-\lambda) f(b).$$ On remarque en effet que
$$(\lambda a + (1-\lambda) b, \lambda f(a) + (1-\lambda) f(b)) = \lambda (a, f(a)) + (1-\lambda) (b, f(b))$$ est le point du segment de droite reliant $(a,f(a))$ à $(b,f(b))$ d'abscisse $\lambda a + (1-\lambda) b$. Par ailleurs, $f(\lambda a + (1-\lambda) b)$ est la valeur de la fonction $f$ en ce même point. L'inégalité signifie donc que les segments de droite reliant deux points du graphe de $f$ ont tous leurs points au dessus du graphe.
Une fonction est par contre dite concave si l'ensemble des points en dessous du graphe de $f$ forme un ensemble convexe. Attention : cela ne revient pas à demander que l'ensemble des points au dessus du graphe est concave ! Contrairement aux ensembles qui sont soit convexes, soit concaves, il existe donc des fonctions qui ne sont ni convexes ni concaves.
Convexité et dérivée
Lorsqu'une fonction est (deux fois) dérivable, on peut facilement savoir si elle est convexe, concave, ou aucun des deux.Proposition
Soit $f: I \subseteq \mathbb{R} \to \mathbb{R}$ une fonction.
- Si $f$ est dérivable sur $I$, alors $f$ est convexe (respectivement concave) si et seulement si $f'$ est croissante (resp. décroissante) sur $I$.
- Si $f$ est deux fois dérivable, alors $f$ est convexe (respectivement concave) si et seulement si $f''(x) \geq 0$ (resp. $f''(x) \leq 0)$ $\forall x \in I$.
Lors d'une compétition, il n'est cependant pas réellement nécessaire de prouver qu'une fonction basique est concave ou convexe. En effet, on sait qu'il suffit de dériver deux fois la fonction pour démontrer qu'elle est convexe ou concave, ce qui se fait de manière automatique.
En pratique, on dessine le graphe de la fonction pour voir si elle est convexe ou concave en regardant l'ensemble délimité par le graphe. Il n'est donc pas important de connaître les dérivées : il faut juste retenir que la convexité ou concavité d'une fonction peut être vérifiée rigoureusement à l'aide des dérivées.
Si la fonction qui nous intéresse est par contre plus exotique comme par exemple $\displaystyle f : x \mapsto \frac{x^4}{24} + \frac{p^2x^2}{4} - \frac{px^3}{6}$ (pour un paramètre $p$), il faudra tout de même calculer $\displaystyle f''(x) = \frac{x^2 + p^2}{2} - xp$ et montrer que $f''$ est positif pour démontrer que $f$ est convexe.
Il est cependant rare d'être dans un tel cas et une vérification graphique suffit généralement amplement. La connaissance des dérivées n'est donc pas du tout nécessaire pour continuer à explorer les inégalités !
Remarque : Les fonctions $f$ vérifiant $f''(x) = 0$ $\forall x \in I$ sont convexes et concaves. Il s'agit en fait des fonctions affines $f(x) = ax + b$ dont le graphe est une droite.
Exemples :
- $f:\mathbb{R}\to\mathbb{R}:x\mapsto x^2$ est convexe car sa dérivée $f''(x) = 2$ est positive.
- $f:\mathbb{R}\to\mathbb{R}:x\mapsto e^x$ est convexe car sa dérivée $f''(x) = e^x$ est positive.
- $f:\mathbb{R}_0^+\to\mathbb{R}:x\mapsto \ln(x)$ est concave car sa dérivée $f''(x) = \frac{-1}{x^2}$ est négative.