Angles
Angles dans un cercle
Un cercle est toujours annonciateur de nombreux angles de même amplitude. Commençons par rappeler quelques mots de vocabulaire.
Si $O$ est le centre du cercle, l'angle $\widehat{AOC}$ possède aussi un nom : il s'agit de l'angle au centre interceptant l'arc $AC$.
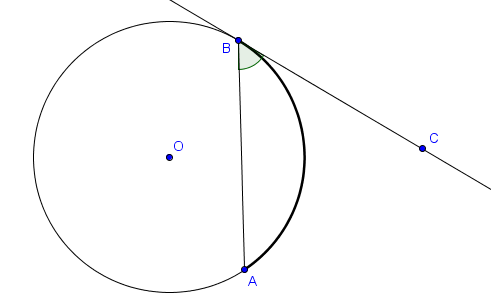
Enfin, dans la situation représentée ci-dessous impliquant une droite tangente au cercle en un point $B$, l'angle $\widehat{ABC}$ est cette fois dit tangentiel et interceptant l'arc $AB$.
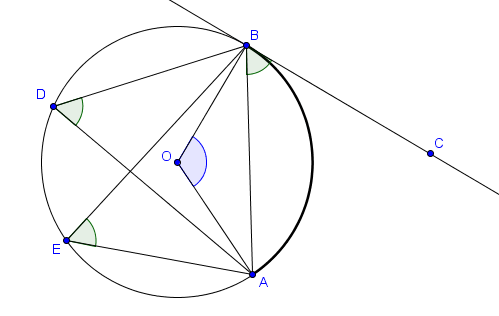
Sur la figure suivante, on a donc
$$\displaystyle\frac{\widehat{AOB}}{2} = \widehat{AEB} = \widehat{ADB} = \widehat{ABC}$$ car tous ces angles interceptent l'arc $AB$. Remarquons cependant que si $F$ était un point du petit arc $AB$, alors $\widehat{AFB}$ intercepterait cette fois-ci le grand arc $AB$ et ne pourrait donc pas être inclus dans la suite d'égalité. En fait, on verra plus tard qu'on a dans ce cas $\widehat{AFB} = 180^° - \widehat{AEB}$.
Vocabulaire
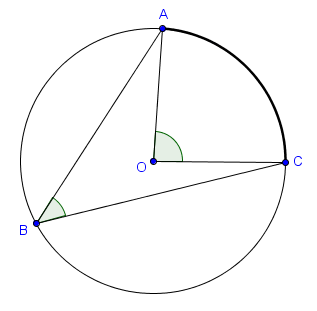
Si $A$, $B$ et $C$ sont trois points sur un cercle, l'angle $\widehat{ABC}$ est appelé angle inscrit au cercle. L'arc intercepté par $\widehat{ABC}$ est par définition l'arc de cercle $AC$ ne contenant pas le point $B$. Celui-ci est représenté en gras sur la figure ci-dessous.
Si $O$ est le centre du cercle, l'angle $\widehat{AOC}$ possède aussi un nom : il s'agit de l'angle au centre interceptant l'arc $AC$.
Enfin, dans la situation représentée ci-dessous impliquant une droite tangente au cercle en un point $B$, l'angle $\widehat{ABC}$ est cette fois dit tangentiel et interceptant l'arc $AB$.

Propriétés
Lorsque des angles, qu'ils soient inscrits, au centre ou tangentiels, interceptent un même arc, alors on peut en déduire des égalités à propos de leur amplitude. Plus précisément, on a les propriétés suivantes. Les angles dont nous parlons sont bien sûr toujours sur un unique cercle.Propriété (angles inscrits)
Des angles inscrits interceptant le même arc ont même amplitude.
Propriété (angles au centre et inscrit)
Si un angle au centre et un angle inscrit interceptent le même arc, alors l'amplitude de l'angle au centre est double de celle de l'angle inscrit.
Propriété (angles tangentiel et inscrit)
Un angle inscrit et un angle tangentiel interceptant le même arc ont même amplitude.
Sur la figure suivante, on a donc
$$\displaystyle\frac{\widehat{AOB}}{2} = \widehat{AEB} = \widehat{ADB} = \widehat{ABC}$$ car tous ces angles interceptent l'arc $AB$. Remarquons cependant que si $F$ était un point du petit arc $AB$, alors $\widehat{AFB}$ intercepterait cette fois-ci le grand arc $AB$ et ne pourrait donc pas être inclus dans la suite d'égalité. En fait, on verra plus tard qu'on a dans ce cas $\widehat{AFB} = 180^° - \widehat{AEB}$.
