Quadrilatères cycliques
Premières propriétés
Un quadrilatère cyclique, parfois aussi appelé quadrilatère inscriptible, est un quadrilatère pouvant être inscrit dans un cercle. Cette nouvelle notion peut a priori sembler peu utile, mais c'est pourtant tout le contraire. Nous verrons dans la section suivante comment elle peut servir dans la résolution d'un problème. Nous exhibons d'abord quelques propriétés fondamentales des quadrilatères cycliques.
Cette propriété est triviale puisque, le quadrilatère $ABCD$ étant inscriptible, les deux angles cités sont des angles inscrits interceptant l'arc $AD$. En fait, nous verrons que la réciproque est également vraie, ce qui est moins évident.
Là aussi, nous allons voir que la réciproque est également vraie.
Propriété 1
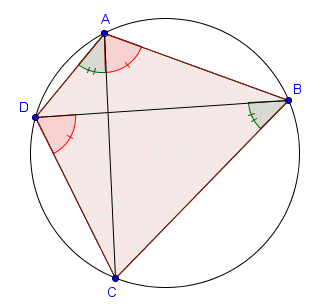
Soit $ABCD$ un quadrilatère cyclique. On a $\widehat{ABD} = \widehat{ACD}$.
Cette propriété est triviale puisque, le quadrilatère $ABCD$ étant inscriptible, les deux angles cités sont des angles inscrits interceptant l'arc $AD$. En fait, nous verrons que la réciproque est également vraie, ce qui est moins évident.
Propriété 2
Les angles opposés d'un quadrilatère cyclique sont supplémentaires. Autrement dit, si $ABCD$ est cyclique, alors $\widehat{DAB}+\widehat{BCD} = 180^\circ$.

Démonstration
En considérant les angles du triangle $BCD$, on a
$$\widehat{BCD} = 180^\circ - \widehat{DBC} - \widehat{BDC}$$ Or, on a $\widehat{DBC} = \widehat{DAC}$ et $\widehat{BDC} = \widehat{BAC}$ (égalités d'angles inscrits), d'où
$$\widehat{BCD} = 180^\circ - \widehat{DAC} - \widehat{BAC} = 180^\circ - \widehat{DAB}$$ comme voulu.
$$\widehat{BCD} = 180^\circ - \widehat{DBC} - \widehat{BDC}$$ Or, on a $\widehat{DBC} = \widehat{DAC}$ et $\widehat{BDC} = \widehat{BAC}$ (égalités d'angles inscrits), d'où
$$\widehat{BCD} = 180^\circ - \widehat{DAC} - \widehat{BAC} = 180^\circ - \widehat{DAB}$$ comme voulu.
Là aussi, nous allons voir que la réciproque est également vraie.