Triangles
Droites et points particuliers
Dans un triangle, on peut tracer les trois médiatrices, les trois bissectrices, les trois hauteurs ou les trois médianes. Dans tous les cas, les trois droites s'intersectent en un point particulier.

Bissectrices (intérieure et extérieure) d'un angle.
Dans un triangle, l'intersection des bissectrices intérieures des trois angles est assez connue, mais on peut en fait également considérer l'intersection de deux bissectrices extérieures avec la dernière bissectrice intérieure.
On peut bien sûr interchanger $A$, $B$ et $C$ dans la deuxième partie de l'énoncé, et on a donc trois cercles exinscrits à un triangle donné. La démonstration du fait que ces droites se rencontrent est à nouveau une conséquence directe de la définition des bissectrices. Chacun des quatre points particuliers que nous venons d'exhiber est à distance égale des trois droites $AB$, $AC$ et $BC$. Ils sont donc chacun le centre d'un cercle tangent à ces trois droites (d'où leurs noms : centre du cercle inscrit et centres des cercles exinscrits). Quoique les cercles exinscrits soient moins connus que le cercle inscrit, ceux-ci peuvent se révéler utiles dans des problèmes légèrement avancés.
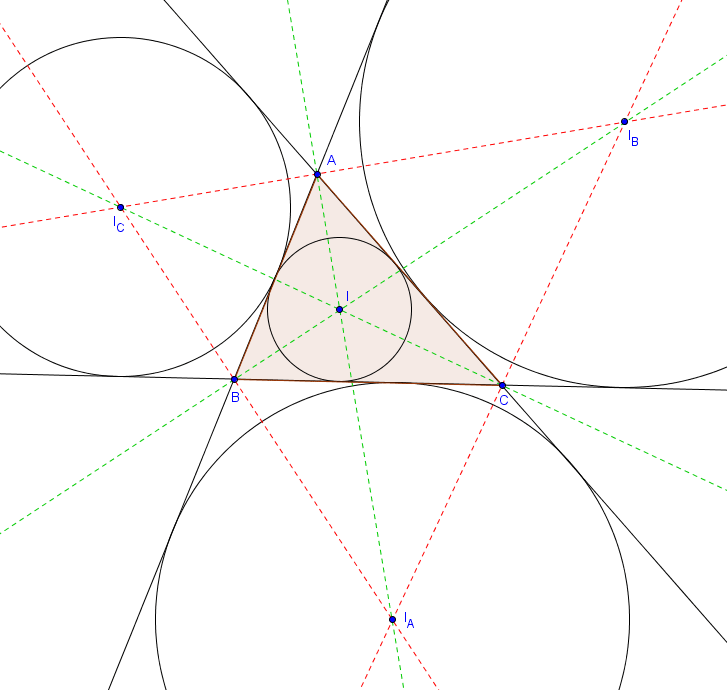
Centres du cercle inscrit et des cercles exinscrits.
Médiatrices et centre du cercle circonscrit
Rappelons que la médiatrice d'un segment $[AB]$ est le lieu des points situés à égale distance de $A$ et de $B$. Il s'agit de la droite perpendiculaire à $[AB]$ et passant par son milieu.Propriété (médiatrices)
Les médiatrices des trois côtés d'un triangle se rencontrent en un point : le centre du cercle circonscrit au triangle.
Démonstration
Par définition des médiatrices, il est évident que les trois droites se coupent en un point. En effet, si on note $ABC$ le triangle, alors l'intersection de la médiatrice de $[AB]$ et de la médiatrice de $[AC]$ est un point se situant à égale distance de $A$ et de $B$, et à égale distance de $A$ et de $C$. Par conséquent, il est aussi à égale distance de $B$ et de $C$ et appartient donc à la médiatrice de $[BC]$. On note généralement ce point commun $O$. Puisqu'il est situé à égale distance des trois sommets $A$, $B$ et $C$, on peut tracer le cercle de centre $O$ et de rayon $|OA| = |OB| = |OC|$ : il s'agira du cercle circonscrit au triangle $ABC$.
Bissectrices, centre du cercle inscrit et centres des cercles exinscrits
On définit généralement la bissectrice d'un angle comme étant la droite coupant cet angle en deux. En fait, on peut dire que la bissectrice de l'angle $\widehat{BAC}$ est le lieu des points situés à égale distance de la droite $AB$ et de la droite $AC$, mais cela donne lieu à un phénomène légèrement différent. En effet, ce lieu ainsi défini consiste en fait en deux droites et non une, comme l'indique la figure suivante. Ces deux droites sont perpendiculaires. La droite dessinée en vert est appelée bissectrice intérieure alors que celle dessinée en rouge est appelée bissectrice extérieure. La plupart du temps, on oublie cette bissectrice extérieure et parle uniquement de bissectrice en désignant la bissectrice intérieure.
Bissectrices (intérieure et extérieure) d'un angle.
Dans un triangle, l'intersection des bissectrices intérieures des trois angles est assez connue, mais on peut en fait également considérer l'intersection de deux bissectrices extérieures avec la dernière bissectrice intérieure.
Propriété (bissectrices)
Les trois bissectrices intérieures d'un triangle $ABC$ se rencontrent en un point : le centre du cercle inscrit au triangle. De plus, les bissectrices extérieures de $A$ et de $B$ et la bissectrice intérieure de $C$ se rencontrent en un point : le centre d'un cercle exinscrit au triangle.
On peut bien sûr interchanger $A$, $B$ et $C$ dans la deuxième partie de l'énoncé, et on a donc trois cercles exinscrits à un triangle donné. La démonstration du fait que ces droites se rencontrent est à nouveau une conséquence directe de la définition des bissectrices. Chacun des quatre points particuliers que nous venons d'exhiber est à distance égale des trois droites $AB$, $AC$ et $BC$. Ils sont donc chacun le centre d'un cercle tangent à ces trois droites (d'où leurs noms : centre du cercle inscrit et centres des cercles exinscrits). Quoique les cercles exinscrits soient moins connus que le cercle inscrit, ceux-ci peuvent se révéler utiles dans des problèmes légèrement avancés.

Centres du cercle inscrit et des cercles exinscrits.
Hauteurs et orthocentre
Comme pour les médiatrices et les bissectrices, les trois hauteurs d'un triangle sont concourantes.Propriété (hauteurs)
Les trois hauteurs d'un triangle se rencontrent en un point : l'orthocentre du triangle.
Démonstration
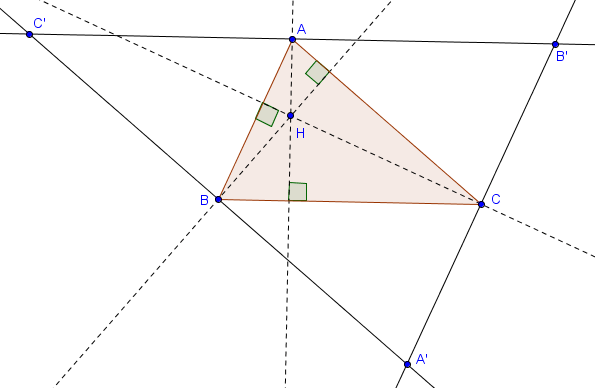
Cette fois, le fait que les trois hauteurs se rencontrent n'est pas une conséquence directe de leur définition. Il existe cependant une astuce pour montrer ce fait en utilisant le résultat comme quoi les médiatrices d'un triangle sont concourantes. En effet, étant donné un triangle $ABC$, on peut tracer la droite parallèle à $BC$ passant par $A$, celle parallèle à $AC$ passant par $B$ et celle parallèle à $AB$ passant par $C$. Ces trois droites délimitent un triangle $A'B'C'$, comme sur la figure suivante.
Or, on constate aisément que les triangles $ABC'$, $AB'C$ et $A'BC$ sont tous isométriques au triangle $ABC$. Cela implique notamment que $|C'B| = |BA'|$ et par conséquent que la hauteur de $ABC$ issue de $B$ n'est rien d'autre que la médiatrice de $[A'C']$. De la même façon, les deux autres hauteurs de $ABC$ sont les deux autres médiatrices de $A'B'C'$. Les trois hauteurs de $ABC$ se rencontrent donc en le centre du cercle circonscrit à $A'B'C'$.
Or, on constate aisément que les triangles $ABC'$, $AB'C$ et $A'BC$ sont tous isométriques au triangle $ABC$. Cela implique notamment que $|C'B| = |BA'|$ et par conséquent que la hauteur de $ABC$ issue de $B$ n'est rien d'autre que la médiatrice de $[A'C']$. De la même façon, les deux autres hauteurs de $ABC$ sont les deux autres médiatrices de $A'B'C'$. Les trois hauteurs de $ABC$ se rencontrent donc en le centre du cercle circonscrit à $A'B'C'$.

Médianes et centre de gravité
Finalement, on a encore le résultat pour les médianes (les droites reliant un sommet au milieu du segment opposé). Nous ne démontrons pas celui-ci maintenant : cela sera en fait une conséquence directe du théorème de Ceva que nous démontrerons plus tard dans ce cours.Propriété (médianes)
Les trois médianes d'un triangle se rencontrent en un point : le centre de gravité du triangle.