Triangles
Propriétés diverses
Nous évoquons finalement quelques propriétés intéressantes apparaissant dans les triangles.
La condition $|AB| \neq |AC|$ dans la deuxième partie assure que la bissectrice extérieure de $A$ ne soit pas parallèle à $BC$.
Cette fois, la condition $|AB| \neq |AC|$ assure que la bissectrice intérieure et la médiatrice ne soient pas confondues.
Théorème de la bissectrice
Le théorème de la bissectrice s'énonce comme suit. La deuxième partie est moins connue que la première, mais elle n'en est pas moins intéressante.Théorème de la bissectrice
Soit $ABC$ un triangle.
- L'intersection $A'$ de la bissectrice intérieure de $A$ avec $BC$ est telle que
$$\frac{|A'B|}{|A'C|} = \frac{|AB|}{|AC|}.$$ - Si $|AB| \neq |AC|$, alors l'intersection $A''$ de la bissectrice extérieure de $A$ avec $BC$ est telle que
$$\frac{|A''B|}{|A''C|} = \frac{|AB|}{|AC|}.$$
La condition $|AB| \neq |AC|$ dans la deuxième partie assure que la bissectrice extérieure de $A$ ne soit pas parallèle à $BC$.
Démonstration
On note $\alpha = \widehat{BAA'} = \widehat{CAA'}$.
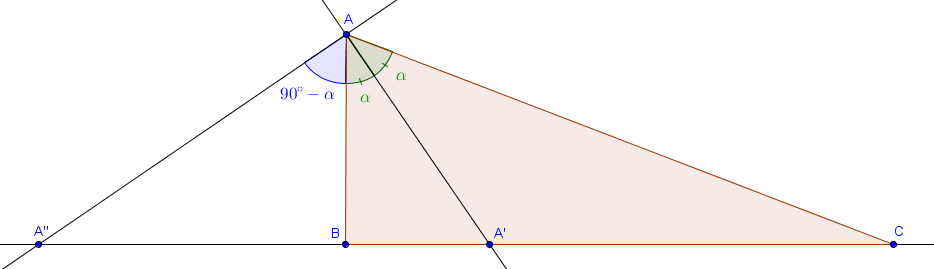

- On applique simplement la loi des sinus dans le triangle $A'BA$ et le triangle $A'CA$, ce qui donne :
$$\frac{|A'B|}{\sin \alpha} = \frac{|AB|}{\sin \widehat{AA'B}} \quad \text{ et } \quad \frac{|A'C|}{\sin \alpha} = \frac{|AC|}{\sin \widehat{AA'C}}.$$ Il suffit alors de remarquer que les angles $\widehat{AA'B}$ et $\widehat{AA'C}$ sont supplémentaires (et ont donc le même sinus) et de combiner les deux égalités pour trouver
$$\frac{|A'B|}{|A'C|} = \frac{|AB|}{|AC|}.$$ - Nous donnons la démonstration dans le cas où $|AB| < |AC|$, la situation étant symétrique. On utilise cette fois la loi des sinus dans le triangle $A''BA$ et le triangle $A''CA$ pour obtenir :
$$\frac{|A''B|}{\sin (90^\circ-\alpha)} = \frac{|AB|}{\sin \widehat{AA''B}} \quad \text{ et } \quad \frac{|A''C|}{\sin (90^\circ+\alpha)} = \frac{|AC|}{\sin \widehat{AA''C}}.$$ On conclut alors de la même façon qu'au premier point, vu que $\sin (90^\circ-\alpha) = \sin (90^\circ+\alpha)$.
Intersection d'une bissectrice avec la médiatrice opposée
Un autre résultat qu'il est primordial de connaître est le suivant.Théorème
Soit $ABC$ un triangle. Si $|AB| \neq |AC|$, alors la bissectrice intérieure de $A$ rencontre la médiatrice de $[BC]$ en un point du cercle circonscrit à $ABC$. Il en est de même pour la bissectrice extérieure.
Cette fois, la condition $|AB| \neq |AC|$ assure que la bissectrice intérieure et la médiatrice ne soient pas confondues.
Démonstration
Pour montrer ce résultat, nous allons voir les choses un peu autrement. En effet, nous notons $X$ et $X'$ les intersections de la médiatrice de $[BC]$ avec le cercle circonscrit à $ABC$ comme sur la figure suivante, et nous allons montrer que $X$ se situe sur la bissectrice intérieure de $A$ alors que $X'$ se situe sur la bissectrice extérieure. C'est bien sûr équivalent à ce que l'on désire montrer.
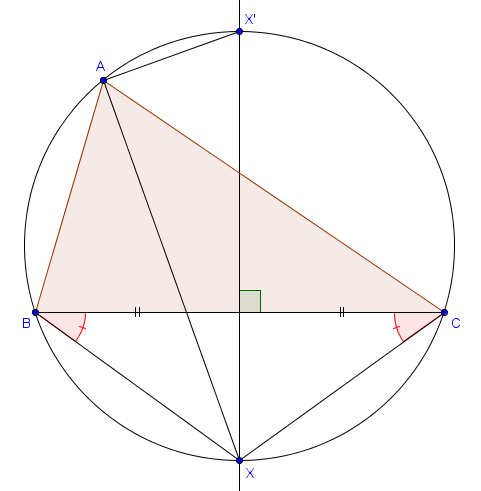
Vu que $X$ se situe sur la médiatrice de $[BC]$, le triangle $BXC$ est isocèle et on a donc $\widehat{XBC} = \widehat{XCB}$. Or, puisque $X$ est aussi sur le cercle circonscrit à $ABC$, on a également $\widehat{XBC} = \widehat{XAC}$ et $\widehat{XCB} = \widehat{XAB}$. Au final, on a ainsi $\widehat{XAB} = \widehat{XAC}$ ce qui montre que $X$ se situe sur la bissectrice intérieure de $A$.
D'autre part, vu que $XX'$ est la médiatrice de $[BC]$, elle passe par le centre $O$ du cercle circonscrit et est dès lors un diamètre de ce cercle. Le triangle $XAX'$ est donc rectangle car inscrit dans un demi-cercle, ce qui montre que $\widehat{XAX'} = 90^\circ$. Puisque $AX$ est la bissectrice intérieure de $A$, $AX'$ ne peut être que sa bissectrice extérieure.

Vu que $X$ se situe sur la médiatrice de $[BC]$, le triangle $BXC$ est isocèle et on a donc $\widehat{XBC} = \widehat{XCB}$. Or, puisque $X$ est aussi sur le cercle circonscrit à $ABC$, on a également $\widehat{XBC} = \widehat{XAC}$ et $\widehat{XCB} = \widehat{XAB}$. Au final, on a ainsi $\widehat{XAB} = \widehat{XAC}$ ce qui montre que $X$ se situe sur la bissectrice intérieure de $A$.
D'autre part, vu que $XX'$ est la médiatrice de $[BC]$, elle passe par le centre $O$ du cercle circonscrit et est dès lors un diamètre de ce cercle. Le triangle $XAX'$ est donc rectangle car inscrit dans un demi-cercle, ce qui montre que $\widehat{XAX'} = 90^\circ$. Puisque $AX$ est la bissectrice intérieure de $A$, $AX'$ ne peut être que sa bissectrice extérieure.