Rapports de section
Prérequis
Résumé
Nous introduisons dans ce chapitre les rapports de section. Nous énonçons ensuite en termes de ceux-ci les théorèmes de Ceva et de Ménélaüs, constituant des armes redoutables pour montrer que trois droites sont concourantes ou que trois points sont alignés.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Définition et propriétés
On commence par définir la notion de rapport orienté entre deux segments parallèles.
Par exemple, dans la figure suivante où $C$, $D$, $E$ et $F$ sont alignés, $AB$ est parallèle à $CF$ et $|CD| = |EF| = 2|DE| = 2|AB|$, on a
$$ \frac{\overline{AB}}{\overline{DE}} = 1, \quad \frac{\overline{CD}}{\overline{FE}} = -1, \quad \frac{\overline{AB}}{\overline{DF}}= \frac{1}{3}, \quad \frac{\overline{CF}}{\overline{BA}} = -5.$$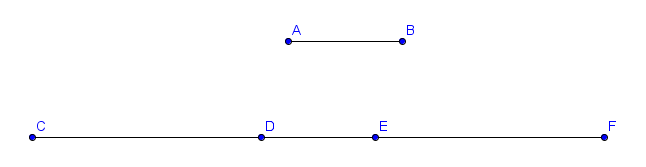
Remarque : Il s'agit bien de rapports, au sens où on a la formule $\displaystyle\frac{\overline{AB}}{\overline{CD}} \cdot \frac{\overline{CD}}{\overline{EF}} = \frac{\overline{AB}}{\overline{EF}}$ lorsque les droites $AB$, $CD$ et $EF$ sont parallèles.
On peut maintenant définir la notion de rapport de section.
On peut par exemple réécrire le théorème de la bissectrice à l'aide des rapports de section. En effet, si dans un triangle $ABC$, $A'$ désigne l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ désigne l'intersection de la bissectrice extérieure de $A$ avec $BC$, le théorème de la bissectrice nous indique que
$$r_{BC}(A') = -\frac{b}{c} \quad \text{ et } \quad r_{BC}(A'') = \frac{b}{c}$$ où $b = |AC|$ et $c = |AB|$.
Il est intéressant de regarder comment $r_{AB}(C)$ varie lorsque $A$ et $B$ sont fixés et que $C$ varie sur la droite $AB$. Ceci est représenté sur le graphique suivant.
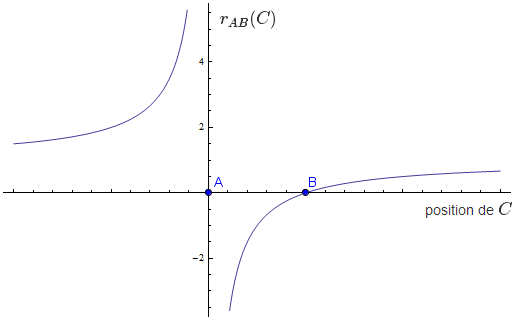
Rapport de section $r_{AB}(C)$ en fonction de la position de $C$.
En fait, il n'est pas compliqué de se convaincre que $r_{AB}(C)$ peut prendre n'importe quelle valeur réelle différente de $1$. Ce qui rend le rapport de section digne d'intérêt est que le rapport de section d'un point par rapport à deux points fixés détermine univoquement la position du point (autrement dit, la fonction tracée ci-dessus est injective). Dès lors, pour montrer que deux points sont égaux, on peut simplement montrer que leurs rapports de section par rapport à deux mêmes points sont égaux.
Définition (rapport orienté)
Soit $A$, $B$, $C$ et $D$ quatre points distincts deux à deux et tels que $AB$ est parallèle à $CD$. Le rapport orienté $\displaystyle \frac{\overline{AB}}{\overline{CD}}$ est défini par
$$ \frac{\overline{AB}}{\overline{CD}} = \left\{\begin{array}{cl}
\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans le même sens,} \\
-\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans des sens opposés.}
\end{array}\right.$$
$$ \frac{\overline{AB}}{\overline{CD}} = \left\{\begin{array}{cl}
\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans le même sens,} \\
-\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans des sens opposés.}
\end{array}\right.$$
Par exemple, dans la figure suivante où $C$, $D$, $E$ et $F$ sont alignés, $AB$ est parallèle à $CF$ et $|CD| = |EF| = 2|DE| = 2|AB|$, on a
$$ \frac{\overline{AB}}{\overline{DE}} = 1, \quad \frac{\overline{CD}}{\overline{FE}} = -1, \quad \frac{\overline{AB}}{\overline{DF}}= \frac{1}{3}, \quad \frac{\overline{CF}}{\overline{BA}} = -5.$$

Remarque : Il s'agit bien de rapports, au sens où on a la formule $\displaystyle\frac{\overline{AB}}{\overline{CD}} \cdot \frac{\overline{CD}}{\overline{EF}} = \frac{\overline{AB}}{\overline{EF}}$ lorsque les droites $AB$, $CD$ et $EF$ sont parallèles.
On peut maintenant définir la notion de rapport de section.
Définition (rapport de section)
Si $C$ est un point de $AB$ distinct de $A$, alors le rapport de section $r_{AB}(C)$ de $C$ par rapport à $A$ et $B$ est défini par
$$r_{AB}(C) = \frac{\overline{CB}}{\overline{CA}}.$$
$$r_{AB}(C) = \frac{\overline{CB}}{\overline{CA}}.$$
On peut par exemple réécrire le théorème de la bissectrice à l'aide des rapports de section. En effet, si dans un triangle $ABC$, $A'$ désigne l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ désigne l'intersection de la bissectrice extérieure de $A$ avec $BC$, le théorème de la bissectrice nous indique que
$$r_{BC}(A') = -\frac{b}{c} \quad \text{ et } \quad r_{BC}(A'') = \frac{b}{c}$$ où $b = |AC|$ et $c = |AB|$.
Il est intéressant de regarder comment $r_{AB}(C)$ varie lorsque $A$ et $B$ sont fixés et que $C$ varie sur la droite $AB$. Ceci est représenté sur le graphique suivant.
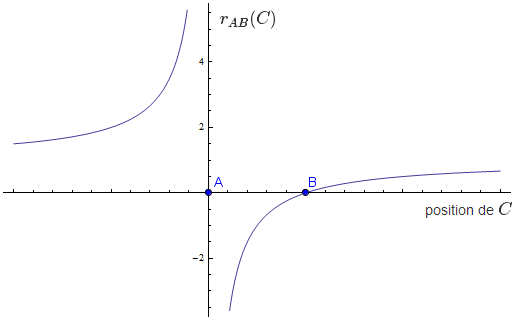
Rapport de section $r_{AB}(C)$ en fonction de la position de $C$.
En fait, il n'est pas compliqué de se convaincre que $r_{AB}(C)$ peut prendre n'importe quelle valeur réelle différente de $1$. Ce qui rend le rapport de section digne d'intérêt est que le rapport de section d'un point par rapport à deux points fixés détermine univoquement la position du point (autrement dit, la fonction tracée ci-dessus est injective). Dès lors, pour montrer que deux points sont égaux, on peut simplement montrer que leurs rapports de section par rapport à deux mêmes points sont égaux.
2. Théorème de Ceva
Le théorème de Ceva donne une condition nécessaire et suffisante pour que trois droites issues des trois sommets d'un triangle soient concourantes (ou parallèles dans un cas dégénéré, bien qu'il puisse également servir).
Un corollaire immédiat de ce théorème est que les trois médianes d'un triangle sont concourantes. En effet, le rapport de section du milieu d'un côté par rapport aux deux sommets de ce côté vaut $-1$, et le produit donne donc trivialement $-1$, ce qui prouve que les médianes sont concourantes.
Cette version trigonométrique peut dans certains cas être préférable. Par exemple, une conséquence directe de ce résultat est que les bissectrices (intérieures) d'un triangle sont concourantes. On ne pouvait pas le déduire immédiatement de la première version de Ceva.
Théorème de Ceva
Soit $ABC$ un triangle et $D \in BC$, $E \in AC$, $F \in AB$ des points distincts des sommets. Les droites $AD$, $BE$ et $CF$ sont concourantes ou parallèles si et seulement si
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = -1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = -1.$$
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = -1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = -1.$$
Un corollaire immédiat de ce théorème est que les trois médianes d'un triangle sont concourantes. En effet, le rapport de section du milieu d'un côté par rapport aux deux sommets de ce côté vaut $-1$, et le produit donne donc trivialement $-1$, ce qui prouve que les médianes sont concourantes.
Démonstration
Nous démontrons le théorème de Ceva dans le cas où les points $D$, $E$ et $F$ sont situés sur les côtés du triangle et non à l'extérieur. Le lecteur doit cependant garder à l'esprit que celui-ci reste valide même lorsque $D$, $E$ ou $F$ se situe sur les prolongements des côtés.
Dans ce cas particulier, les droites ne seront bien sûr jamais parallèles, et le produit des trois rapports de sections sera toujours négatif (en tant que produit de trois nombres négatifs). Nous devons donc simplement montrer que les droites $AD$, $BE$ et $CF$ sont concourantes si et seulement si
$$\frac{|FB|}{|FA|} \cdot \frac{|DC|}{|DB|} \cdot \frac{|EA|}{|EC|} = 1.$$ Commençons par l'implication $\Rightarrow$. On suppose donc que les trois droites se rencontrent en un point $M$, et on cherche à montrer que le produit vaut $1$. On s'intéresse pour cela aux aires des différents triangles présents dans la figure.
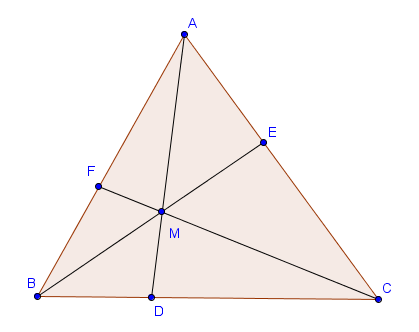
Les triangles $BDM$ et $CDM$ ayant la même hauteur, le rapport de leurs aires est égal au rapport de leurs bases :
$$\frac{S(BDM)}{S(CDM)} = \frac{|BD|}{|DC|}.$$ On peut faire la même constatation pour les triangles $BDA$ et $CDA$ :
$$\frac{S(BDA)}{S(CDA)} = \frac{|BD|}{|DC|}.$$ Dès lors, le triangle $BMA$ pouvant être obtenu comme différence des triangles $BDA$ et $BDM$, tout comme $CMA$ qui est la différence des triangles $CDA$ et $CDM$, on garde le même rapport :
$$\frac{S(BMA)}{S(CMA)} = \frac{|BD|}{|DC|}.$$ Or, ce raisonnement est également valable sur les deux autres côtés du triangle, et on a donc aussi les relations
$$\frac{S(CMB)}{S(AMB)} = \frac{|CE|}{|EA|} \quad \text{ et } \quad \frac{S(AMC)}{S(BMC)} = \frac{|AF|}{|BF|}.$$ En multipliant les trois dernières égalités, on a la formule voulue (après passage à l'inverse).
Passons à l'implication $\Leftarrow$. On suppose cette fois que
$$\frac{|FB|}{|FA|} \cdot \frac{|DC|}{|DB|} \cdot \frac{|EA|}{|EC|} = 1,$$ et on cherche à montrer que les trois droites sont concourantes. Pour ce faire, on note $M$ le point d'intersection des droites $BE$ et $CF$, et ensuite $D'$ l'intersection de $AM$ avec $BC$. Il suffit alors de montrer que $D = D'$. Par l'autre partie de la preuve, vu que $AD'$, $BE$ et $CF$ sont concourantes, on sait que
$$\frac{|FB|}{|FA|} \cdot \frac{|D'C|}{|D'B|} \cdot \frac{|EA|}{|EC|} = 1.$$ On en déduit que
$$ \frac{|DC|}{|DB|} = \frac{|D'C|}{|D'B|}.$$ Autrement dit, $D$ et $D'$ ont le même rapport de section par rapport à $B$ et $C$ : on a donc $D = D'$ comme désiré.
Dans ce cas particulier, les droites ne seront bien sûr jamais parallèles, et le produit des trois rapports de sections sera toujours négatif (en tant que produit de trois nombres négatifs). Nous devons donc simplement montrer que les droites $AD$, $BE$ et $CF$ sont concourantes si et seulement si
$$\frac{|FB|}{|FA|} \cdot \frac{|DC|}{|DB|} \cdot \frac{|EA|}{|EC|} = 1.$$ Commençons par l'implication $\Rightarrow$. On suppose donc que les trois droites se rencontrent en un point $M$, et on cherche à montrer que le produit vaut $1$. On s'intéresse pour cela aux aires des différents triangles présents dans la figure.

Les triangles $BDM$ et $CDM$ ayant la même hauteur, le rapport de leurs aires est égal au rapport de leurs bases :
$$\frac{S(BDM)}{S(CDM)} = \frac{|BD|}{|DC|}.$$ On peut faire la même constatation pour les triangles $BDA$ et $CDA$ :
$$\frac{S(BDA)}{S(CDA)} = \frac{|BD|}{|DC|}.$$ Dès lors, le triangle $BMA$ pouvant être obtenu comme différence des triangles $BDA$ et $BDM$, tout comme $CMA$ qui est la différence des triangles $CDA$ et $CDM$, on garde le même rapport :
$$\frac{S(BMA)}{S(CMA)} = \frac{|BD|}{|DC|}.$$ Or, ce raisonnement est également valable sur les deux autres côtés du triangle, et on a donc aussi les relations
$$\frac{S(CMB)}{S(AMB)} = \frac{|CE|}{|EA|} \quad \text{ et } \quad \frac{S(AMC)}{S(BMC)} = \frac{|AF|}{|BF|}.$$ En multipliant les trois dernières égalités, on a la formule voulue (après passage à l'inverse).
Passons à l'implication $\Leftarrow$. On suppose cette fois que
$$\frac{|FB|}{|FA|} \cdot \frac{|DC|}{|DB|} \cdot \frac{|EA|}{|EC|} = 1,$$ et on cherche à montrer que les trois droites sont concourantes. Pour ce faire, on note $M$ le point d'intersection des droites $BE$ et $CF$, et ensuite $D'$ l'intersection de $AM$ avec $BC$. Il suffit alors de montrer que $D = D'$. Par l'autre partie de la preuve, vu que $AD'$, $BE$ et $CF$ sont concourantes, on sait que
$$\frac{|FB|}{|FA|} \cdot \frac{|D'C|}{|D'B|} \cdot \frac{|EA|}{|EC|} = 1.$$ On en déduit que
$$ \frac{|DC|}{|DB|} = \frac{|D'C|}{|D'B|}.$$ Autrement dit, $D$ et $D'$ ont le même rapport de section par rapport à $B$ et $C$ : on a donc $D = D'$ comme désiré.
Version trigonométrique
Il existe aussi une formulation trigonométrique au théorème de Ceva. La démonstration consiste simplement à appliquer la loi des sinus judicieusement, et est laissée au lecteur.Théorème de Ceva (version trigonométrique)
Soit $ABC$ un triangle et $D \in [BC]$, $E \in [AC]$, $F \in [AB]$ des points distincts des sommets. Les droites $AD$, $BE$ et $CF$ sont concourantes si et seulement si
$$\frac{\sin \widehat{FCB}}{\sin \widehat{FCA}} \cdot \frac{\sin\widehat{DAC}}{\sin \widehat{DAB}} \cdot \frac{\sin \widehat{EBA}}{\sin \widehat{EBC}} = 1.$$
$$\frac{\sin \widehat{FCB}}{\sin \widehat{FCA}} \cdot \frac{\sin\widehat{DAC}}{\sin \widehat{DAB}} \cdot \frac{\sin \widehat{EBA}}{\sin \widehat{EBC}} = 1.$$
Cette version trigonométrique peut dans certains cas être préférable. Par exemple, une conséquence directe de ce résultat est que les bissectrices (intérieures) d'un triangle sont concourantes. On ne pouvait pas le déduire immédiatement de la première version de Ceva.
3. Théorème de Ménélaüs
Le théorème de Ménélaüs est très similaire au théorème de Céva. Il donne cette fois une condition nécessaire et suffisante pour que trois points situés sur les côtés d'un triangle (ou sur leur prolongement) soient alignés.
Théorème de Ménélaüs
Soit $ABC$ un triangle et $D \in BC$, $E \in AC$, $F \in AB$ des points distincts des sommets. Les points $D$, $E$ et $F$ sont alignés si et seulement si
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = 1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = 1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Démonstration
Comme pour Ceva, on commence par le sens $\Rightarrow$. Notons $X$ l'intersection de $DF$ avec la parallèle à $BC$ passant par $A$, comme sur la figure ci-dessous.
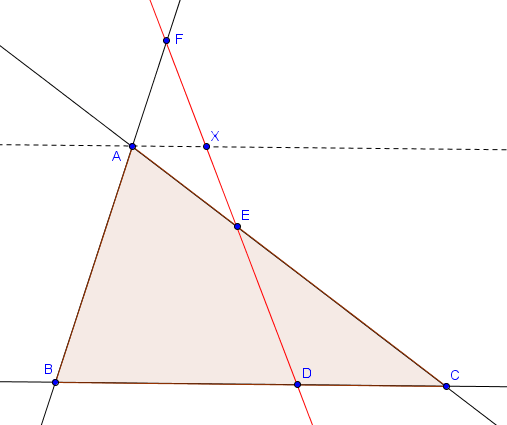
Par Thalès dans les triangles $BDF$ et $CDE$, on a les deux relations suivantes :
$$\frac{\overline{DB}}{\overline{XA}} = \frac{\overline{FB}}{\overline{FA}} \quad \text{ et } \quad \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{EA}}{\overline{EC}}.$$ On a donc
$$\frac{\overline{DB}}{\overline{DC}} = \frac{\overline{DB}}{\overline{XA}} \cdot \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{EA}}{\overline{EC}},$$ ce qui est équivalent à
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Passons au sens $\Leftarrow$. On suppose donc avoir
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$ Remarquons déjà que $EF$ ne peut pas être parallèle à $BC$. En effet, si tel était le cas, par Thalès on aurait
$$\frac{\overline{EA}}{\overline{EC}} = \frac{\overline{FA}}{\overline{FB}},$$ d'où $\displaystyle \frac{\overline{DC}}{\overline{DB}} = 1$ mais cela est impossible car un rapport de section ne vaut jamais $1$. On peut donc noter $D'$ l'intersection de $EF$ avec $BC$, et on montre comme dans la démonstration du théorème de Ceva que l'on a forcément $D = D'$.

Par Thalès dans les triangles $BDF$ et $CDE$, on a les deux relations suivantes :
$$\frac{\overline{DB}}{\overline{XA}} = \frac{\overline{FB}}{\overline{FA}} \quad \text{ et } \quad \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{EA}}{\overline{EC}}.$$ On a donc
$$\frac{\overline{DB}}{\overline{DC}} = \frac{\overline{DB}}{\overline{XA}} \cdot \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{EA}}{\overline{EC}},$$ ce qui est équivalent à
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Passons au sens $\Leftarrow$. On suppose donc avoir
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$ Remarquons déjà que $EF$ ne peut pas être parallèle à $BC$. En effet, si tel était le cas, par Thalès on aurait
$$\frac{\overline{EA}}{\overline{EC}} = \frac{\overline{FA}}{\overline{FB}},$$ d'où $\displaystyle \frac{\overline{DC}}{\overline{DB}} = 1$ mais cela est impossible car un rapport de section ne vaut jamais $1$. On peut donc noter $D'$ l'intersection de $EF$ avec $BC$, et on montre comme dans la démonstration du théorème de Ceva que l'on a forcément $D = D'$.