Triangles (suite)
Triangle podaire et droite de Simson
Étant donné un triangle $ABC$ et un point $P$ quelconque dans le plan, on appelle triangle podaire relatif à $P$ le triangle $A'B'C'$ dont les sommets $A'$, $B'$ et $C'$ sont les projections orthogonales de $P$ sur $BC$, $AC$ et $AB$, respectivement.
Sur la figure suivante, le point $P$ est à l'intérieur du triangle, mais il peut tout à fait se situer à l'extérieur.
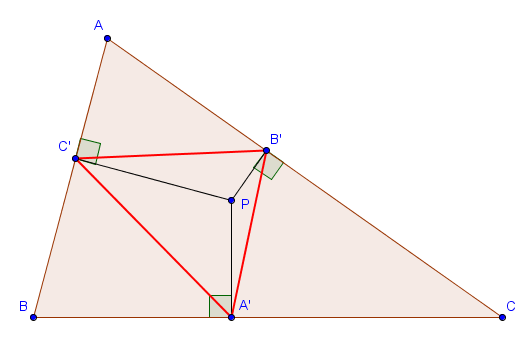
Les triangles podaires apparaîssent parfois dans des problèmes de géométrie. Une première remarque que l'on peut toujours faire est que, dans une telle situation, les quadrilatères $AB'PC'$, $BC'PA'$ et $CA'PB'$ sont toujours cycliques, de diamètres respectifs $[AP]$, $[BP]$ et $[CP]$. Cette information permet notamment de trouver les longueurs des côtés du triangle podaire $A'B'C'$ en fonction d'autres paramètres. En effet, par la loi des sinus dans le triangle $AB'C'$, on a par exemple
$$|B'C'| = |PA| \cdot \sin A$$ (où $|PA|$ prend le rôle de $2R$ dans la loi des sinus).
Observons à présent les propriétés des triangles podaires relatifs à certains points particuliers du triangle.
Sur la figure suivante, le point $P$ est à l'intérieur du triangle, mais il peut tout à fait se situer à l'extérieur.

Les triangles podaires apparaîssent parfois dans des problèmes de géométrie. Une première remarque que l'on peut toujours faire est que, dans une telle situation, les quadrilatères $AB'PC'$, $BC'PA'$ et $CA'PB'$ sont toujours cycliques, de diamètres respectifs $[AP]$, $[BP]$ et $[CP]$. Cette information permet notamment de trouver les longueurs des côtés du triangle podaire $A'B'C'$ en fonction d'autres paramètres. En effet, par la loi des sinus dans le triangle $AB'C'$, on a par exemple
$$|B'C'| = |PA| \cdot \sin A$$ (où $|PA|$ prend le rôle de $2R$ dans la loi des sinus).
Observons à présent les propriétés des triangles podaires relatifs à certains points particuliers du triangle.
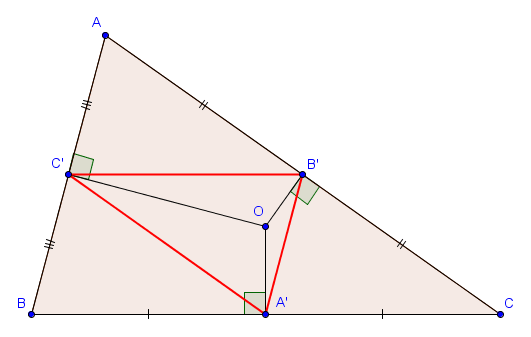
- Si $P = O$, le centre du cercle circonscrit à $ABC$, alors comme $O$ se situe sur les médiatrices des différents côtés, les points $A'$, $B'$ et $C'$ sont les milieux des côtés $[BC]$, $[AC]$ et $[AB]$, respectivement.
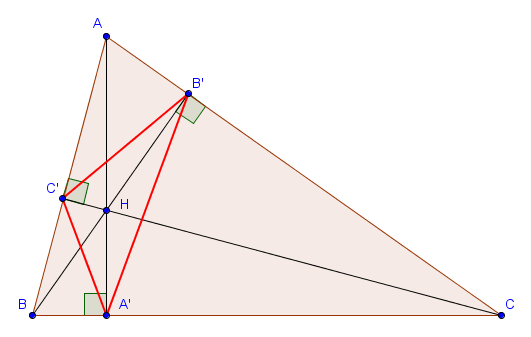
Dans ce cas, la situation est très claire. En effet, par Thalès, $B'C'$ est parallèle à $BC$, $A'C'$ est parallèle à $AC$ et $A'B'$ est parallèle à $AB$. Le triangle $A'B'C'$ est donc semblable à $ABC$ (avec un rapport $\frac{1}{2}$). De plus, le point $O$ n'est rien d'autre que l'orthocentre du triangle $A'B'C'$, puisque $A'O$ est perpendiculaire à $BC$ et donc également à $B'C'$. (et de même pour $B'O$ et $C'O$). En fait, on se rend compte que la construction que nous venons de faire est exactement la construction inverse de celle que nous avons faite pour prouver que les trois hauteurs d'un triangle sont concourantes. - Si $P = H$, l'orthocentre de $ABC$, alors les points $A'$, $B'$ et $C'$ sont les pieds des hauteurs issues de $A$, $B$ et $C$, respectivement. Le triangle $A'B'C'$ est également appelé dans ce cas le triangle orthique.
Afin que $H$ reste à l'intérieur de $ABC$, nous supposons dorénavant que le triangle $ABC$ est acutangle. On peut alors utiliser le fait que $AB'HC'$ et $CA'HB'$ sont cycliques pour trouver :
$$\widehat{HB'C'} = \widehat{HAC'} = 90^\circ - \widehat{ABC},$$ $$\widehat{HB'A'} = \widehat{HCA'} = 90^\circ - \widehat{ABC}.$$ Nous venons donc de montrer que $H$ est sur la bissectrice de l'angle $\widehat{A'B'C'}$. De la même manière, il est sur les deux autres bissectrices du triangle podaire et on en déduit que $H$ est en fait le centre du cercle inscrit à $A'B'C'$. (Attention : cela n'est vrai que si $ABC$ est acutangle.)
Droite de Simson
Nous parlons de triangle podaire, mais il n'est a priori pas impossible que, pour un certain choix de $P$, les points $A'$, $B'$ et $C'$ soient alignés ! Dans un tel cas, on ne parle plus réellement de triangle podaire, mais plutôt de droite de Simson associée à $P$. En fait, il existe une condition nécessaire et suffisante sur $P$ pour que le triangle podaire se transforme en droite de Simson :Théorème (droite de Simson)
Soit $ABC$ un triangle et $P$ un point quelconque du plan. Les projections $A'$, $B'$ et $C'$ du point $P$ sur les droites $BC$, $AC$ et $AB$ respectivement sont alignées si et seulement si $P$ appartient au cercle circonscrit au triangle $ABC$.
Démonstration
Nous donnons la démonstration en supposant que les différents points sont situés comme sur la figure suivante (c'est-à-dire tels que $B' \in [AC]$ et $A' \in [BC]$ mais $A \in [BC']$).
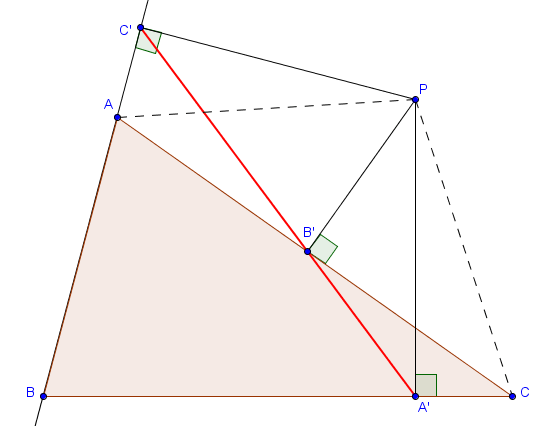
Les trois points $A'$, $B'$ et $C'$ sont alors alignés si et seulement si $\widehat{PB'A'} + \widehat{PB'C'} = 180^\circ$.
Or, le quadrilatère $PB'A'C$ étant cyclique, on a
$$\widehat{PB'A'} = 180^\circ - \widehat{PCA'} = 180^\circ - \widehat{PCB}.$$ De la même façon, $PB'AC'$ est cyclique et on en déduit
$$\widehat{PB'C'} = \widehat{PAC'} = 180^\circ - \widehat{PAB}.$$ Les trois points sont donc alignés si et seulement si $\widehat{PCB} + \widehat{PAB} = 180^\circ$, ce qui revient exactement à dire que $P$ se situe sur le cercle circonscrit à $ABC$.

Les trois points $A'$, $B'$ et $C'$ sont alors alignés si et seulement si $\widehat{PB'A'} + \widehat{PB'C'} = 180^\circ$.
Or, le quadrilatère $PB'A'C$ étant cyclique, on a
$$\widehat{PB'A'} = 180^\circ - \widehat{PCA'} = 180^\circ - \widehat{PCB}.$$ De la même façon, $PB'AC'$ est cyclique et on en déduit
$$\widehat{PB'C'} = \widehat{PAC'} = 180^\circ - \widehat{PAB}.$$ Les trois points sont donc alignés si et seulement si $\widehat{PCB} + \widehat{PAB} = 180^\circ$, ce qui revient exactement à dire que $P$ se situe sur le cercle circonscrit à $ABC$.