Triangles (suite)
Triangle tangentiel
À un triangle $ABC$, on peut associer un autre triangle, dit triangle tangentiel. Pour le définir, il suffit de considérer $\Gamma$ le cercle circonscrit à $ABC$ et de tracer les tangentes à $\Gamma$ en $A$, $B$ et $C$. Celles-ci forment un triangle, et c'est celui-ci que l'on appelle triangle tangentiel.
Lien avec les symédianes
On peut retrouver, en construisant le triangle tangentiel, les symédianes d'un triangle.Proposition (triangle tangentiel et symédianes)
Soit $A'B'C'$ le triangle tangentiel associé à $ABC$ (de sorte que $A \in [B'C']$, $B \in [A'C']$ et $C \in [A'B']$). Les droites $AA'$, $BB'$ et $CC'$ sont les symédianes du triangle $ABC$.
Démonstration
Montrons que $AA'$ est la symédiane de $ABC$ partant de $A$. Pour ce faire, il suffit de prouver que $A'$ est le milieu d'une antiparallèle à $BC$. Traçons donc simplement l'antiparallèle à $BC$ passant par $A'$. On note $B''$ l'intersection de celle-ci avec $AB$ et $C''$ son intersection avec $AC$, et il faut prouver que $|B''A'| = |A'C''|$.
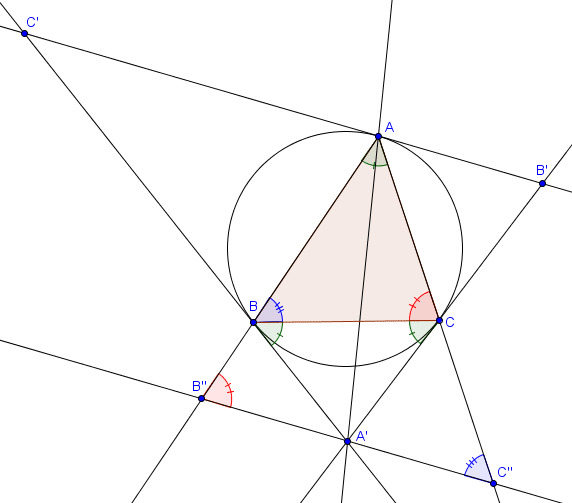
Par définition d'antiparallèle, on a $\widehat{AB''A'} = \widehat{ACB}$ et $\widehat{AC''A'} = \widehat{ABC}$. De plus, comme $\widehat{A'BC} = \widehat{BAC}$ (angles tangentiel et inscrit), on trouve
$$\widehat{B''BA'} = 180^\circ - \widehat{A'BC} - \widehat{CBA} = 180^\circ - \widehat{BAC} - \widehat{CBA} = \widehat{ACB} = \widehat{AB''A'}.$$ On en déduit que $BA'B''$ est isocèle, et de la même façon que $CA'C''$ est isocèle. On a donc
$$|A'B''| = |A'B| = |A'C| = |A'C''|,$$ comme voulu.

Par définition d'antiparallèle, on a $\widehat{AB''A'} = \widehat{ACB}$ et $\widehat{AC''A'} = \widehat{ABC}$. De plus, comme $\widehat{A'BC} = \widehat{BAC}$ (angles tangentiel et inscrit), on trouve
$$\widehat{B''BA'} = 180^\circ - \widehat{A'BC} - \widehat{CBA} = 180^\circ - \widehat{BAC} - \widehat{CBA} = \widehat{ACB} = \widehat{AB''A'}.$$ On en déduit que $BA'B''$ est isocèle, et de la même façon que $CA'C''$ est isocèle. On a donc
$$|A'B''| = |A'B| = |A'C| = |A'C''|,$$ comme voulu.
Lien avec le triangle orthique
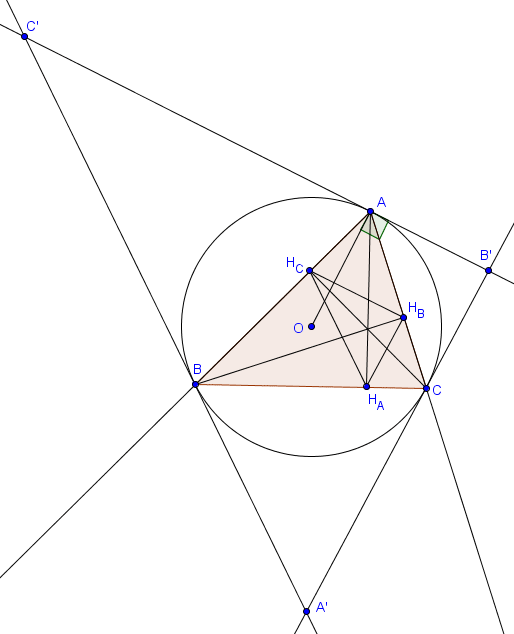
On peut également remarquer que le triangle tangentiel est semblable au triangle orthique. En fait, on a plus précisément le résultat suivant.Proposition (triangles tangentiel et orthique)
Les côtés du triangle tangentiel sont parallèles aux côtés du triangle orthique.
Démonstration
Notons $H_A$, $H_B$ et $H_C$ les pieds des hauteurs de $ABC$. On doit montrer que $H_BH_C$ est parallèle à $B'C'$. Si $O$ désigne le centre du cercle circonscrit à $ABC$, on sait que $OA$ est perpendiculaire à $B'C'$. Il suffit donc de prouver que $OA$ est également perpendiculaire à $H_BH_C$. Il s'agit en fait d'une simple chasse aux angles. En effet, on a
$$\widehat{H_BH_CA} = \widehat{ACB}$$ car $BH_CH_BC$ est cyclique et
$$\widehat{H_CAO} = \frac{180^\circ-\widehat{AOB}}{2} = 90^\circ - \widehat{ACB},$$ d'où $\widehat{H_BH_CA} + \widehat{H_CAO} = 90^\circ$, ce qui suffit à prouver que $H_BH_C$ est perpendiculaire à $AO$.
$$\widehat{H_BH_CA} = \widehat{ACB}$$ car $BH_CH_BC$ est cyclique et
$$\widehat{H_CAO} = \frac{180^\circ-\widehat{AOB}}{2} = 90^\circ - \widehat{ACB},$$ d'où $\widehat{H_BH_CA} + \widehat{H_CAO} = 90^\circ$, ce qui suffit à prouver que $H_BH_C$ est perpendiculaire à $AO$.
