Dénombrement (suite)
Inclusion-exclusion
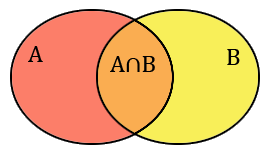
Le principe d'inclusion-exclusion est une formule permettant de calculer le nombre d'éléments dans une union d'ensembles à partir du nombre d'éléments dans leurs différentes intersections. L'exemple le plus simple consiste en deux ensembles $A$ et $B$. S'ils sont disjoints (ils n'ont aucun élément en commun), alors on a bien sûr $|A \cup B| = |A| + |B|$. Par contre, s'ils ont des éléments communs, alors en calculant cette somme $|A|+|B|$, on compte deux fois les éléments qui sont dans $A \cap B$ (c'est-à-dire dans $A$ et $B$ à la fois). Il faut donc retirer le nombre d'éléments communs aux deux ensembles, et on a la formule générale suivante :
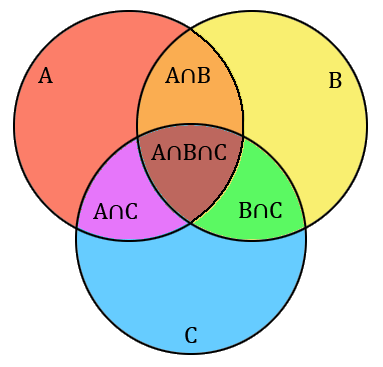
On peut faire le même raisonnement pour trois ensembles $A$, $B$ et $C$. On commence par calculer la somme $|A| + |B| + |C|$, mais encore une fois on a compté plus d'une fois les éléments se situant dans deux ensembles à la fois. On retranche donc $|A \cap B| + |B \cap C| + |C \cap A|$ du résultat. Mais si maintenant, on considère les éléments se situant dans les trois ensembles à la fois, alors on les a compté trois fois chacun lors de la première somme avant de les retrancher trois fois : on n'a donc au final pas compté ces éléments ! Il faut donc à nouveau compter les éléments de $A \cap B \cap C$, ce qui donne la formule suivante :
On comprend mieux le terme inclusion-exclusion, puisqu'on ajoute certains termes avant d'en retrancher d'autres, puis d'en rajouter à nouveau.
Ce raisonnement se généralise en fait à $n$ ensembles :
Cette formule peut sembler compliquée mais elle ne fait que généraliser les formules que nous avons vues pour $n = 2$ et $n= 3$. En effet, pour $k = 1$ on retrouve tous les ensembles seuls, pour $k = 2$, on a $(-1)^{2-1} = -1$ et on retire donc les cardinaux de toutes les intersections deux par deux, puis pour $k = 3$ on rajoute les intersections trois par trois, et ainsi de suite jusqu'à l'intersection de tous les ensembles.
L'erreur type est de se dire "Il y a $500$ nombres pairs, $333$ nombres divisibles par $3$ et $200$ nombres divisibles par $5$, donc la réponse est $500+333+200=1033$." Évidemment, on constate immédiatement que le raisonnement est erroné puisqu'on obtient une réponse supérieure à $1000$. Le problème est que nous avons compté plusieurs fois les nombres multiples de $6$, de $10$ ou de $15$ : il s'agit exactement du principe de l'inclusion-exclusion.
Il existe aussi des exemples du même type que ceux que nous avons rencontrés jusqu'à présent, comme le suivant.
Principe d'inclusion-exclusion (pour $2$ ensembles)
$$|A \cup B| = |A| + |B| - |A \cap B|.$$

On peut faire le même raisonnement pour trois ensembles $A$, $B$ et $C$. On commence par calculer la somme $|A| + |B| + |C|$, mais encore une fois on a compté plus d'une fois les éléments se situant dans deux ensembles à la fois. On retranche donc $|A \cap B| + |B \cap C| + |C \cap A|$ du résultat. Mais si maintenant, on considère les éléments se situant dans les trois ensembles à la fois, alors on les a compté trois fois chacun lors de la première somme avant de les retrancher trois fois : on n'a donc au final pas compté ces éléments ! Il faut donc à nouveau compter les éléments de $A \cap B \cap C$, ce qui donne la formule suivante :
Principe d'inclusion-exclusion (pour $3$ ensembles)
$$|A \cup B \cup C| = |A| + |B| + |C| - |A\cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$
On comprend mieux le terme inclusion-exclusion, puisqu'on ajoute certains termes avant d'en retrancher d'autres, puis d'en rajouter à nouveau.

Ce raisonnement se généralise en fait à $n$ ensembles :
Principe d'inclusion-exclusion (pour $n$ ensembles)
Soient $A_1, \ldots, A_n$ des ensembles. On a
$$|A_1 \cup \ldots \cup A_n| = \sum_{k=1}^n \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq n} |A_{i_1} \cap \ldots \cap A_{i_k}| \right).$$
$$|A_1 \cup \ldots \cup A_n| = \sum_{k=1}^n \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq n} |A_{i_1} \cap \ldots \cap A_{i_k}| \right).$$
Cette formule peut sembler compliquée mais elle ne fait que généraliser les formules que nous avons vues pour $n = 2$ et $n= 3$. En effet, pour $k = 1$ on retrouve tous les ensembles seuls, pour $k = 2$, on a $(-1)^{2-1} = -1$ et on retire donc les cardinaux de toutes les intersections deux par deux, puis pour $k = 3$ on rajoute les intersections trois par trois, et ainsi de suite jusqu'à l'intersection de tous les ensembles.
Application en combinatoire
Voici un exemple assez connu où le principe d'inclusion-exclusion se révèle très utile :Problème
Combien y a-t-il de nombres compris entre $1$ et $1000$ divisibles par $2$, par $3$ ou par $5$ ?
L'erreur type est de se dire "Il y a $500$ nombres pairs, $333$ nombres divisibles par $3$ et $200$ nombres divisibles par $5$, donc la réponse est $500+333+200=1033$." Évidemment, on constate immédiatement que le raisonnement est erroné puisqu'on obtient une réponse supérieure à $1000$. Le problème est que nous avons compté plusieurs fois les nombres multiples de $6$, de $10$ ou de $15$ : il s'agit exactement du principe de l'inclusion-exclusion.
Solution
Notons $A$ l'ensemble des nombres (entre $1$ et $1000$) pairs, $B$ l'ensemble des nombres multiples de $3$ et $C$ l'ensemble des nombres multiples de $5$. Nous cherchons alors le cardinal de $A \cup B \cup C$, et le principe d'inclusion-exclusion s'applique :
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$ Or, on a $|A| = 500$, $|B| = 333$, $|C| = 200$, $|A \cap B| = 166$ (car $A \cap B$ est l'ensemble des nombres multiples de $6$), $|B \cap C| = 66$, $|C \cap A| = 100$ et $|A \cap B \cap C| = 33$, d'où au final
$$|A \cup B \cup C| = 500+333+200-166-66-100+33=\boxed{734}.$$
$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|.$$ Or, on a $|A| = 500$, $|B| = 333$, $|C| = 200$, $|A \cap B| = 166$ (car $A \cap B$ est l'ensemble des nombres multiples de $6$), $|B \cap C| = 66$, $|C \cap A| = 100$ et $|A \cap B \cap C| = 33$, d'où au final
$$|A \cup B \cup C| = 500+333+200-166-66-100+33=\boxed{734}.$$
Il existe aussi des exemples du même type que ceux que nous avons rencontrés jusqu'à présent, comme le suivant.
Problème
Je possède $8$ photos différentes de mes vacances, et je désire les distribuer à mes $5$ amis. Pour que tout le monde soit content, chaque ami doit recevoir au moins une photo. De combien de manières puis-je effectuer ma distribution ?
Solution
S'il n'y avait pas la condition comme quoi chaque ami doit recevoir au moins une photo, on pourrait simplement considérer les photos une à une et décider pour chacune à qui on la donne : on aurait donc $5^8$ possibilités. En fait, on peut le voir comme un arrangement avec répétitions de $8$ objets parmi $5$. Le minimum d'une photo par personne nous empêche cependant de procéder de la sorte, et il n'est pas évident de voir comment on pourrait effectuer un comptage direct. Une idée déjà suggérée dans ce chapitre est alors de passer au complémentaire, c'est-à-dire de compter le nombre de façons de distribuer les photos de sorte qu'au moins un ami ne recoive aucune photo. Cela nous fait penser au principe d'inclusion exclusion, puisqu'en notant
$$A_i = \{\text{distributions où l'ami numéro $i$ ne reçoit pas de photo}\},$$ on cherche le cardinal de $A_1 \cup \ldots \cup A_5$. Pour que le principe d'inclusion-exclusion soit utile, il faut qu'il soit facile d'évaluer le cardinal d'une intersection de $A_i$. Mais cela est effectivement aisé ! En effet, le cardinal d'une intersection $A_{i_1} \cap \ldots \cap A_{i_k}$ (avec $k$ ensembles différents) représente le nombre de façons de distribuer $8$ photos à $5$ amis sans en donner aux amis numéro $i_1, \ldots, i_k$. Cela revient à distribuer $8$ photos à $5-k$ amis, et le cardinal vaut donc $(5-k)^8$. Le principe d'inclusion-exclusion donne donc :
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} |A_{i_1} \cap \ldots \cap A_{i_k}| \right) \\
& = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} (5-k)^8 \right)
\end{align}$$ Pour $k$ fixé, les termes de la somme intérieure sont tous identiques (égaux à $(5-k)^8$, et il reste donc juste à évaluer combien il y a de termes dans cette somme. Le nombre de termes est simplement égal au nombre de façons de choisir les indices $i_1, \ldots, i_k$ dans $\{1, \ldots, 5\}$, c'est-à-dire égal à $C^k_5$. On a donc
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \cdot C^k_5 \cdot(5-k)^8 \right) \\[2mm]
&= C^1_5 \cdot 4^8 - C^2_5 \cdot 3^8 + C^3_5 \cdot 2^8 - C^4_5 \cdot 1^8 + C^5_5 \cdot 0^8 \\[2mm]
&= 5\cdot 65536 - 10 \cdot 6561 + 10 \cdot 256 - 5 \cdot 1\\[2mm]
&= 264625
\end{align}$$ La réponse au problème initial est donc $5^8 - 264625 = \boxed{126000}$.
$$A_i = \{\text{distributions où l'ami numéro $i$ ne reçoit pas de photo}\},$$ on cherche le cardinal de $A_1 \cup \ldots \cup A_5$. Pour que le principe d'inclusion-exclusion soit utile, il faut qu'il soit facile d'évaluer le cardinal d'une intersection de $A_i$. Mais cela est effectivement aisé ! En effet, le cardinal d'une intersection $A_{i_1} \cap \ldots \cap A_{i_k}$ (avec $k$ ensembles différents) représente le nombre de façons de distribuer $8$ photos à $5$ amis sans en donner aux amis numéro $i_1, \ldots, i_k$. Cela revient à distribuer $8$ photos à $5-k$ amis, et le cardinal vaut donc $(5-k)^8$. Le principe d'inclusion-exclusion donne donc :
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} |A_{i_1} \cap \ldots \cap A_{i_k}| \right) \\
& = \sum_{k=1}^5 \left( (-1)^{k-1} \sum_{1\leq i_1 < \ \ldots \ < i_k \leq 5} (5-k)^8 \right)
\end{align}$$ Pour $k$ fixé, les termes de la somme intérieure sont tous identiques (égaux à $(5-k)^8$, et il reste donc juste à évaluer combien il y a de termes dans cette somme. Le nombre de termes est simplement égal au nombre de façons de choisir les indices $i_1, \ldots, i_k$ dans $\{1, \ldots, 5\}$, c'est-à-dire égal à $C^k_5$. On a donc
$$\begin{align}
|A_1 \cup \ldots \cup A_5| & = \sum_{k=1}^5 \left( (-1)^{k-1} \cdot C^k_5 \cdot(5-k)^8 \right) \\[2mm]
&= C^1_5 \cdot 4^8 - C^2_5 \cdot 3^8 + C^3_5 \cdot 2^8 - C^4_5 \cdot 1^8 + C^5_5 \cdot 0^8 \\[2mm]
&= 5\cdot 65536 - 10 \cdot 6561 + 10 \cdot 256 - 5 \cdot 1\\[2mm]
&= 264625
\end{align}$$ La réponse au problème initial est donc $5^8 - 264625 = \boxed{126000}$.