Pavages
Cases deux à deux non recouvrables
Pour illustrer une autre méthode, examinons un autre problème classique.
Encore une fois, quelques essais suffisent à se convaincre qu'il ne va pas être possible de paver le carré $3 \times 3$ à l'aide de ces pavés. On peut également compter que si un tel pavage existait, alors il serait constitué de $\frac{9}{3} = 3$ pavés. Comme le nombre de pavés est assez réduit, il est cette fois envisageable de traiter les différents cas, mais cela reste laborieux et le risque d'effectuer une erreur est assez grand.
Au vu de la section précédente, on peut aussi être tenté de colorier le carré $3 \times 3$. Le problème est qu'ici, chaque pavé recouvre $3$ cases. Il faudrait donc pour bien faire utiliser trois couleurs, mais on remarque vite qu'il n'est pas possible de trouver un coloriage pour lequel n'importe quel pavé recouvrirait forcément trois cases de couleurs distinctes. La méthode du coloriage ne semble donc pas efficace face à ce problème.
Il existe une autre méthode permettant de démontrer la non-existence d'un pavage. Dans notre exemple, on a remarqué qu'un éventuel pavage serait constitué d'exactement trois pavés. Or, le carré $3 \times 3$ possède $4$ coins, et l'astuce est de constater que deux coins différents ne peuvent pas être recouverts par un seul et même pavé ! Il est donc impossible, à l'aide d'uniquement $3$ pavés, de recouvrir les $4$ coins de notre surface, et nous avons par conséquent montré que le pavage était impossible.
De manière plus générale, cette méthode consiste, si le nombre de pavés est égal à $n$, à mettre en évidence $(n+1)$ cases qui sont deux à deux non recouvrables par un seul et même pavé. Observons par exemple le problème suivant :
En fait, dans ce dernier exemple, la méthode du coloriage aurait pu également fonctionner (et on voit facilement que les méthodes sont équivalentes) :
Dans la preuve précédente, il aurait même été possible de conclure en n'exhibant que les cases rouges, à l'aide du principe des tiroirs ! On se rend effectivement compte que chaque pavé $1 \times 6$ recouvre exactement une case rouge, et on a $11$ telles cases. En supposant qu'un pavage existe, on a donc $12$ chaussettes (pavés) dans $11$ tiroirs (cases rouges), et le principe des tiroirs nous indique qu'il y a au moins deux chaussettes dans le même tiroir, c'est-à-dire au moins deux pavés recouvrant la même case rouge, ce qui est impossible puisqu'on ne veut aucun recouvrement.
Problème
Est-il possible de paver entièrement et sans recouvrement un carré de $3 \times 3$ cases à l'aide de pavés de la forme suivante ?


Encore une fois, quelques essais suffisent à se convaincre qu'il ne va pas être possible de paver le carré $3 \times 3$ à l'aide de ces pavés. On peut également compter que si un tel pavage existait, alors il serait constitué de $\frac{9}{3} = 3$ pavés. Comme le nombre de pavés est assez réduit, il est cette fois envisageable de traiter les différents cas, mais cela reste laborieux et le risque d'effectuer une erreur est assez grand.
Au vu de la section précédente, on peut aussi être tenté de colorier le carré $3 \times 3$. Le problème est qu'ici, chaque pavé recouvre $3$ cases. Il faudrait donc pour bien faire utiliser trois couleurs, mais on remarque vite qu'il n'est pas possible de trouver un coloriage pour lequel n'importe quel pavé recouvrirait forcément trois cases de couleurs distinctes. La méthode du coloriage ne semble donc pas efficace face à ce problème.
Il existe une autre méthode permettant de démontrer la non-existence d'un pavage. Dans notre exemple, on a remarqué qu'un éventuel pavage serait constitué d'exactement trois pavés. Or, le carré $3 \times 3$ possède $4$ coins, et l'astuce est de constater que deux coins différents ne peuvent pas être recouverts par un seul et même pavé ! Il est donc impossible, à l'aide d'uniquement $3$ pavés, de recouvrir les $4$ coins de notre surface, et nous avons par conséquent montré que le pavage était impossible.
De manière plus générale, cette méthode consiste, si le nombre de pavés est égal à $n$, à mettre en évidence $(n+1)$ cases qui sont deux à deux non recouvrables par un seul et même pavé. Observons par exemple le problème suivant :
Problème
Est-il possible de paver entièrement et sans recouvrement un rectangle de $8 \times 9$ cases à l'aide de pavés rectangulaires $1 \times 6$ ?
Solution via cette méthode
Le nombre de pavés doit être égal à $\frac{72}{6} = 12$. Pour appliquer la méthode que nous venons de présenter, il faudrait donc trouver $13$ cases dont deux différentes ne peuvent jamais être recouvertes par un seul pavé $1 \times 6$. On peut en fait facilement trouver les cases suivantes (en orange) :
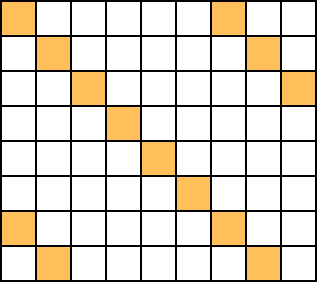
Puisque dans chaque ligne et chaque colonne, il n'y a jamais deux cases oranges situées dans un même rectangle $1 \times 6$, ces cases sont deux à deux non recouvrables par un même pavé de cette forme. On en déduit qu'il n'existe pas de pavage du rectangle $8 \times 9$ comme demandé.
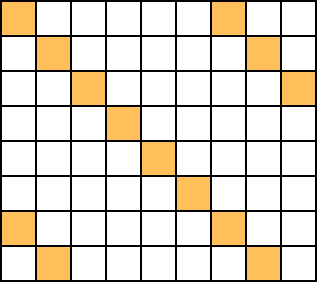
Puisque dans chaque ligne et chaque colonne, il n'y a jamais deux cases oranges situées dans un même rectangle $1 \times 6$, ces cases sont deux à deux non recouvrables par un même pavé de cette forme. On en déduit qu'il n'existe pas de pavage du rectangle $8 \times 9$ comme demandé.
En fait, dans ce dernier exemple, la méthode du coloriage aurait pu également fonctionner (et on voit facilement que les méthodes sont équivalentes) :
Démonstration via un coloriage
On considère le coloriage suivant.

Chaque pavé $1 \times 6$ recouvre six cases de couleurs différentes, et il y a $13$ cases oranges, $13$ cases bleues, $12$ cases vertes, $12$ cases mauves, $11$ cases rouges et $11$ cases blanches. Cela suffit pour conclure qu'un pavage est impossible.

Chaque pavé $1 \times 6$ recouvre six cases de couleurs différentes, et il y a $13$ cases oranges, $13$ cases bleues, $12$ cases vertes, $12$ cases mauves, $11$ cases rouges et $11$ cases blanches. Cela suffit pour conclure qu'un pavage est impossible.
Dans la preuve précédente, il aurait même été possible de conclure en n'exhibant que les cases rouges, à l'aide du principe des tiroirs ! On se rend effectivement compte que chaque pavé $1 \times 6$ recouvre exactement une case rouge, et on a $11$ telles cases. En supposant qu'un pavage existe, on a donc $12$ chaussettes (pavés) dans $11$ tiroirs (cases rouges), et le principe des tiroirs nous indique qu'il y a au moins deux chaussettes dans le même tiroir, c'est-à-dire au moins deux pavés recouvrant la même case rouge, ce qui est impossible puisqu'on ne veut aucun recouvrement.