Invariants et (mono)variants
Monovariants
Un monovariant est, comme un invariant, une quantité que l'on peut calculer à chaque étape. La différence est que sa valeur n'est plus invariante au cours du temps, mais varie de manière monotone (c'est-à-dire croissante ou décroissante). Un monovariant peut par exemple servir pour montrer qu'un processus se termine toujours, comme dans l'exemple suivant.
Problème
Étant donnés $2n$ points distincts du plan, prouver que l'on peut toujours les relier deux par deux par $n$ segments disjoints.
Solution
Ce problème peut sembler a priori très compliqué : comment trouver en toute généralité une façon de relier les $2n$ points sans que les différents segments ne se croisent ? Une façon de faire est de d'abord relier les points deux par deux de manière quelconque, sans se soucier des croisements éventuels, et de tenter de "défaire" tous les croisements que l'on a ainsi créé. On peut par exemple, dès que les segments $[AB]$ et $[CD]$ se croisent, les remplacer par les segments $[AC]$ et $[BD]$ comme sur la figure suivante :
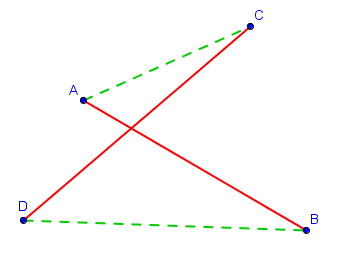
Il reste à montrer qu'à force de défaire les croisements de cette manière, on arrivera toujours à une situation pour laquelle il n'y a plus de croisements. Le monovariant naturel que l'on désire considérer est donc simplement
$$X = \text{nombre de croisements.}$$ La valeur de $X$ est au départ un nombre entier positif et on désire arriver à une situation où $X = 0$. Puisqu'à chaque "décroisement", la valeur de $X$ semble diminuer de $1$, on serait tenté de conclure que notre méthode de "décroisements" successifs aboutira toujours. Ce raisonnement est cependant erroné ! En effet, la valeur de $X$ ne diminue pas forcément à chaque "décroisement", puisqu'il se peut très bien que l'on ait créé de nouveaux croisements en décroisant les deux qui nous intéressaient, comme sur la figure suivante :
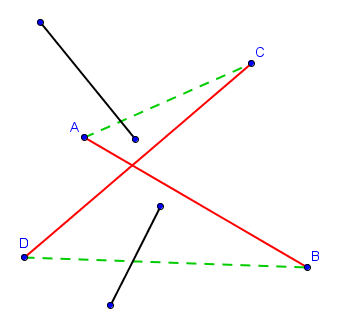
Notre $X$ n'est donc pas un monovariant, puisque sa valeur peut très bien augmenter. Il faut donc trouver quelque chose de plus subtil.
Il n'est pas évident d'y penser, mais un monovariant adéquat dans cette situation est en fait
$$Y = \text{somme des longueurs des $n$ segments.}$$ En effet, lorsque les quatre points $A, B, C, D$ ne sont pas alignés (comme sur nos figures), remplacer $[AB]$ et $[CD]$ (lorsqu'ils se croisent) par $[AC]$ et $[BD]$ diminuera toujours la longueur totale des segments. Il suffit pour le vérifier d'utiliser l'inégalité triangulaire : en notant $E$ l'intersection de $[AB]$ et $[CD]$, on trouve que
$$|AC| + |BD| < |AE| + |EC| + |BE| + |ED| = |AB| + |CD|.$$ Dans le cas où $A, B, C$ et $D$ sont alignés (dans un ordre tel que $[AB]$ et $[CD]$ se croisent), on peut simplement les remplacer par le segment formé des deux "premiers" points et le segment formé par les deux "derniers" points. Là aussi dans tous les cas la somme des longueurs des segments diminue strictement. Notre $Y$ est donc bel et bien un monovariant puisqu'il décroît strictement à chaque fois que l'on défait un croisement.
Ce monovariant implique qu'on ne passera jamais deux fois par la même configuration en décroisant ainsi des segments successivement. Or, il n'existe qu'un nombre fini de manières de relier les $2n$ points par $n$ segments (il y a en fait $(2n-1) \cdot (2n-3) \cdot \ldots \cdot 3\cdot 1$ configurations). Cela signifie que notre processus de décroisement va finir par s'arrêter, et on sera alors dans une situation sans aucun croisement ! Il existe donc bel et bien une façon de relier les $2n$ points par $n$ segments disjoints.

Il reste à montrer qu'à force de défaire les croisements de cette manière, on arrivera toujours à une situation pour laquelle il n'y a plus de croisements. Le monovariant naturel que l'on désire considérer est donc simplement
$$X = \text{nombre de croisements.}$$ La valeur de $X$ est au départ un nombre entier positif et on désire arriver à une situation où $X = 0$. Puisqu'à chaque "décroisement", la valeur de $X$ semble diminuer de $1$, on serait tenté de conclure que notre méthode de "décroisements" successifs aboutira toujours. Ce raisonnement est cependant erroné ! En effet, la valeur de $X$ ne diminue pas forcément à chaque "décroisement", puisqu'il se peut très bien que l'on ait créé de nouveaux croisements en décroisant les deux qui nous intéressaient, comme sur la figure suivante :

Notre $X$ n'est donc pas un monovariant, puisque sa valeur peut très bien augmenter. Il faut donc trouver quelque chose de plus subtil.
Il n'est pas évident d'y penser, mais un monovariant adéquat dans cette situation est en fait
$$Y = \text{somme des longueurs des $n$ segments.}$$ En effet, lorsque les quatre points $A, B, C, D$ ne sont pas alignés (comme sur nos figures), remplacer $[AB]$ et $[CD]$ (lorsqu'ils se croisent) par $[AC]$ et $[BD]$ diminuera toujours la longueur totale des segments. Il suffit pour le vérifier d'utiliser l'inégalité triangulaire : en notant $E$ l'intersection de $[AB]$ et $[CD]$, on trouve que
$$|AC| + |BD| < |AE| + |EC| + |BE| + |ED| = |AB| + |CD|.$$ Dans le cas où $A, B, C$ et $D$ sont alignés (dans un ordre tel que $[AB]$ et $[CD]$ se croisent), on peut simplement les remplacer par le segment formé des deux "premiers" points et le segment formé par les deux "derniers" points. Là aussi dans tous les cas la somme des longueurs des segments diminue strictement. Notre $Y$ est donc bel et bien un monovariant puisqu'il décroît strictement à chaque fois que l'on défait un croisement.
Ce monovariant implique qu'on ne passera jamais deux fois par la même configuration en décroisant ainsi des segments successivement. Or, il n'existe qu'un nombre fini de manières de relier les $2n$ points par $n$ segments (il y a en fait $(2n-1) \cdot (2n-3) \cdot \ldots \cdot 3\cdot 1$ configurations). Cela signifie que notre processus de décroisement va finir par s'arrêter, et on sera alors dans une situation sans aucun croisement ! Il existe donc bel et bien une façon de relier les $2n$ points par $n$ segments disjoints.