Théorie des graphes
Vocabulaire
Un graphe est un ensemble de sommets et d'arêtes reliant certains de ces sommets. La plupart du temps, on demande qu'il n'y ait pas plus d'une arête entre deux sommets et qu'il n'y ait pas de boucle (c'est-à-dire d'arête reliant un sommet à lui-même) : on parle alors de graphe simple. Un exemple de graphe simple est représenté ci-dessous. On dessine généralement un cercle pour chaque sommet, afin de mieux les visualiser, et on les numérote parfois pour mieux les désigner.
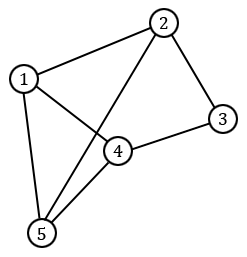
Il existe un certain nombre de mots de vocabulaire concernant les graphes. On dit par exemple que deux sommets sont adjacents s'ils sont reliés par une arête, on parle de chemin pour parler d'une succession d'arêtes dont deux consécutives partagent un sommet, ou encore de cycle pour parler d'un chemin dont le sommet de départ est égal au sommet d'arrivée. Lorsqu'un graphe est simple, on peut simplement désigner un chemin ou un cycle par ses sommets. Par exemple, sur notre graphe ci-dessus, on a $[1, 4, 3]$ qui est un chemin et $[5, 4, 3, 2, 5]$ qui est un cycle. On dit aussi qu'un graphe est connexe si deux sommets quelconques peuvent toujours être joints par un chemin (le graphe ci-dessus est connexe).
Un graphe particulier est le graphe complet à $n$ sommets. Il s'agit du graphe simple possédant $n$ sommets et toutes les $\frac{n(n-1)}{2}$ arêtes possibles entre ces $n$ sommets. On le note généralement $K_n$ et il est bien sûr connexe. Ci-dessous est représenté le graphe complet $K_5$.
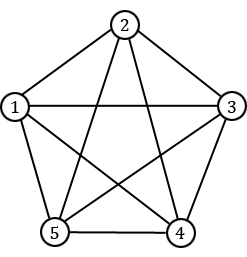
En pratique, il est rare de rencontrer un problème de combinatoire énoncé directement en termes de graphes. En fait, les graphes sont généralement cachés derrière un énoncé plus commun. Par exemple, si l'on parle de $n$ personnes, dont certaines sont amies et d'autres non (l'amitié étant réciproque), alors on peut facilement réexprimer le problème en termes de graphes. En effet, on peut représenter chaque personne par un sommet, et relier deux sommets si et seulement si les deux personnes correspondantes sont amies. On peut alors généralement écrire la thèse en termes de graphes également, et on est ainsi ramené à un problème de pure théorie des graphes.

Il existe un certain nombre de mots de vocabulaire concernant les graphes. On dit par exemple que deux sommets sont adjacents s'ils sont reliés par une arête, on parle de chemin pour parler d'une succession d'arêtes dont deux consécutives partagent un sommet, ou encore de cycle pour parler d'un chemin dont le sommet de départ est égal au sommet d'arrivée. Lorsqu'un graphe est simple, on peut simplement désigner un chemin ou un cycle par ses sommets. Par exemple, sur notre graphe ci-dessus, on a $[1, 4, 3]$ qui est un chemin et $[5, 4, 3, 2, 5]$ qui est un cycle. On dit aussi qu'un graphe est connexe si deux sommets quelconques peuvent toujours être joints par un chemin (le graphe ci-dessus est connexe).
Un graphe particulier est le graphe complet à $n$ sommets. Il s'agit du graphe simple possédant $n$ sommets et toutes les $\frac{n(n-1)}{2}$ arêtes possibles entre ces $n$ sommets. On le note généralement $K_n$ et il est bien sûr connexe. Ci-dessous est représenté le graphe complet $K_5$.

En pratique, il est rare de rencontrer un problème de combinatoire énoncé directement en termes de graphes. En fait, les graphes sont généralement cachés derrière un énoncé plus commun. Par exemple, si l'on parle de $n$ personnes, dont certaines sont amies et d'autres non (l'amitié étant réciproque), alors on peut facilement réexprimer le problème en termes de graphes. En effet, on peut représenter chaque personne par un sommet, et relier deux sommets si et seulement si les deux personnes correspondantes sont amies. On peut alors généralement écrire la thèse en termes de graphes également, et on est ainsi ramené à un problème de pure théorie des graphes.
Remarque
Nous avons ici donné la définition de graphe non-orienté, en ce sens que les arêtes n'ont pas d'orientation. On peut aussi définir les graphes orientés pour lesquels une arête du sommet $a$ vers le sommet $b$ n'est pas la même chose qu'une arête de $b$ vers $a$. On munit alors les arêtes de flèches pour distinguer leur sens. Nous continuerons à analyser les graphes non-orientés dans ce chapitre, mais certains résultats s'écrivent également pour les graphes orientés.