Nombres complexes (forme exponentielle)
Plan complexe
Comme tout nombre complexe peut simplement être considéré comme un couple de nombres réels (sa partie réelle et sa partie imaginaire), on peut penser à $\mathbb{C}$ comme à un plan usuel. On parle alors de plan complexe, et le nombre complexe $x+iy$ est considéré comme le point du plan de coordonnées $(x, y)$. L'axe des abscisses est alors appelé axe des réels puisque l'abscisse d'un point correspond à la partie réelle du nombre correspondant, alors que l'axe des ordonnées est appelé axe des imaginaires pour la même raison.
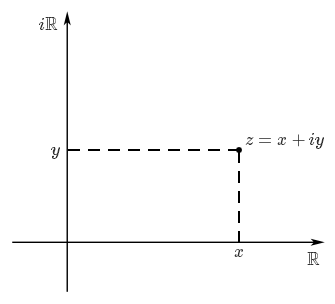
Sur ce plan, il est donc facile de visualiser la partie réelle et la partie imaginaire d'un complexe puisqu'il suffit de projeter le point correspondant sur l'axe voulu. En fait, il est aussi facile de trouver géométriquement le conjugué $\bar z$ d'un nombre complexe $z$, ainsi que son module $|z|$.
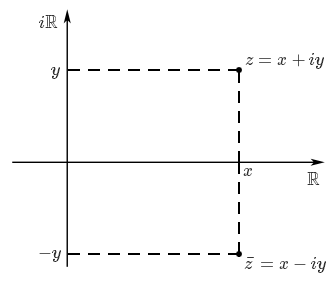
Puisque le conjugué de $z = x+iy$ est $\bar z = x-iy$, il s'agit géométriquement du point symétrique à $z$ par rapport à l'axe des abscisses, comme sur la figure suivante.
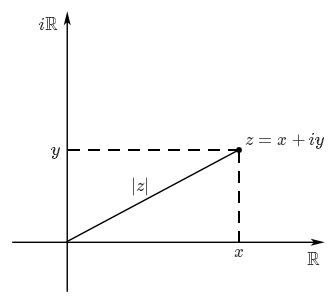
En ce qui concerne le module, on reconnait en la formule $|z| = \sqrt{x^2+y^2}$ la distance entre le point $(x, y)$ et l'origine $(0,0)$. Le module de nombre complexe est donc simplement la distance séparant le point correspondant à l'origine du plan complexe.

Sur ce plan, il est donc facile de visualiser la partie réelle et la partie imaginaire d'un complexe puisqu'il suffit de projeter le point correspondant sur l'axe voulu. En fait, il est aussi facile de trouver géométriquement le conjugué $\bar z$ d'un nombre complexe $z$, ainsi que son module $|z|$.
Puisque le conjugué de $z = x+iy$ est $\bar z = x-iy$, il s'agit géométriquement du point symétrique à $z$ par rapport à l'axe des abscisses, comme sur la figure suivante.

En ce qui concerne le module, on reconnait en la formule $|z| = \sqrt{x^2+y^2}$ la distance entre le point $(x, y)$ et l'origine $(0,0)$. Le module de nombre complexe est donc simplement la distance séparant le point correspondant à l'origine du plan complexe.
