Nombres complexes (forme exponentielle)
Forme trigonométrique
Argument
La représentation des complexes sur le plan peut nous inspirer une vision trigonométrique des nombres complexes. En effet, nous identifions pour le moment un nombre complexe par ses coordonnées cartésiennes $(x, y)$ dans le plan, mais il est aussi possible d'identifier un point $P$ du plan en donnant sa distance par rapport à l'origine $O$ et l'angle que fait $OP$ avec l'axe des abscisses (il s'agit des coordonnées polaires).On sait déjà, lorsque $z \in \mathbb{C}$, que la distance entre le point correspondant et l'origine est donnée par le module $|z|$ de $z$. On définit maintenant l'argument de $z$ (noté $\arg z$) comme étant l'angle déterminé par l'axe des abscisses (sa partie positive) et le segment reliant l'origine à $z$, comme indiqué sur la figure suivante. Cette définition n'a pas réellement de sens pour $z = 0$, c'est pourquoi on considérera toujours à présent des nombres complexes non nuls (sans forcément le mentionner).
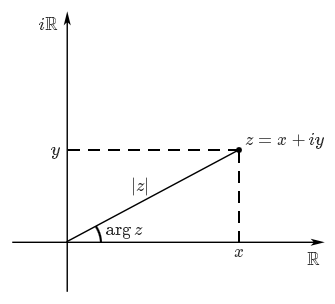
Il s'agit là d'une définition géométrique, mais on peut comme pour le module définir l'argument à partir de $x$ et $y$. Cette partie demande une familiarisation avec les fonctions trigonométriques inverses et n'est pas obligatoire.
Sur la figure précédente, on voit que la tangente de l'angle $\arg z$ est égale à $\displaystyle \frac{y}{x}$ (pourvu que $x$ soit non nul). En se rappelant que l'arctangente d'un nombre réel $x$ est défini comme l'angle de $\displaystyle\left] -\frac{\pi}{2}, \frac{\pi}{2}\right[$ dont la tangente vaut $x$, on peut donc donner la formule suivante pour l'argument de $z = x+iy$ :
$$\arg z = \left\{\begin{array}{cl}
\arctan \left(\frac{y}{x} \right) & \text{ si } \ x > 0, \\
\pi + \arctan \left(\frac{y}{x} \right) & \text{ si } \ x < 0, \\
\frac{\pi}{2} & \text{ si } \ x = 0 \ \text{ et } \ y > 0, \\[1mm]
-\frac{\pi}{2} & \text{ si } \ x = 0 \ \text{ et } \ y < 0.
\end{array}\right.$$ Cette définition est ici donnée à $2\pi$ près, en ce sens que l'angle $\pi$ est par exemple considéré comme identique à l'angle $3\pi$.
Forme trigonométrique des nombres complexes
Nous avons vu comment, à partir de $x$ et $y$, on peut trouver le module et l'argument de $z = x+iy$. Si maintenant, nous connaissons le module $r$ et l'argument $\theta$ d'un nombre complexe $z$, alors on peut retrouver sa forme habituelle $z = x+iy$. En effet, on voit aisément sur la figure précédente que$$\left\{\begin{array}{l}
x = |z| \cdot \cos (\arg z) = r \cos \theta, \\
y = |z| \cdot \sin (\arg z) = r \sin \theta.
\end{array}\right.$$ On dit qu'un nombre complexe $z$ est sous sa forme trigonométrique lorsqu'on l'écrit
$$z = r \cos \theta + i \cdot r \sin \theta = r(\cos \theta + i \sin \theta).$$ Par exemple, le nombre complexe $z = \sqrt{3} - i$ s'écrit sous forme trigonométrique comme
$$z = 2\left(\cos\left(\frac{-\pi}{6}\right) + i \sin \left(\frac{-\pi}{6}\right)\right),$$ puisque son module vaut $\sqrt{\left(\sqrt{3}\right)^2 + (-1)^2} = 2$ et la tangente de son argument vaut $\displaystyle\frac{-1}{\sqrt{3}} = \frac{-\sqrt{3}}{3}$ : on reconnaît la tangente de l'angle $\displaystyle\frac{-\pi}{6}$.