Nombres complexes (forme exponentielle)
Racines $n$-èmes
Nous avons vu que multiplier deux nombres complexes est plus simple sous la forme exponentielle. En particulier, on peut facilement élever un nombre complexe à la puissance $n$ puisqu'on a simplement
$$\left(r \cdot e^{i \theta} \right)^n = r^n \cdot e^{in\theta}.$$ Réciproquement, cela permet d'extraire les racines $n$-èmes d'un nombre complexe très facilement, alors que nous avons vu précédemment qu'extraire une racine carrée était déjà fastidieux sous la forme usuelle. Pour le voir, considérons un nombre complexe non nul $c = r\cdot e^{i \theta}$ et cherchons quelles sont ses racines $n$-èmes. Un nombre $z = s \cdot e^{i \varphi}$ (de module $s$ et d'argument $\varphi$) est racine $n$-ème de $c$ si et seulement si sa $n$-ème puissance vaut $c$, c'est-à-dire si
$$s^n \cdot e^{in\varphi} = r \cdot e^{i\theta}.$$ Les modules doivent être égaux donc $s = \sqrt[n]{r}$, et les arguments aussi d'où $n\varphi = \theta$. Cette dernière égalité n'est cependant pas tout à fait correcte. En effet, nous avons mentionné que nous considérions des angles comme égaux dès qu'ils étaient égaux à un multiple de $2\pi$ près. Il ne faut donc pas avoir $n\varphi = \theta$, mais plutôt $n \varphi = \theta + 2k \pi$ pour un certain $k \in \mathbb{Z}$. Les racines $n$-èmes de $c = r \cdot e^{i \theta}$ sont donc les nombres complexes de la forme (on note $\exp$ au lieu de $e$ pour des raisons pratiques)
$$z_k = \sqrt[n]{r} \cdot \exp\left(i\left(\frac{\theta}{n} + \frac{2k\pi}{n}\right)\right)$$ avec $k \in \mathbb{Z}$. En fait, on voit aisément qu'il n'y a pas une infinité de racines mais exactement $n$, car la valeur de cette expression pour $k = n$ est la même que celle pour $k = 0$. Tout nombre complexe non nul possède donc exactement $n$ racines $n$-èmes, en prenant par exemple $z_0, \ldots, z_{n-1}$.
En particulier, les racines $n$-èmes de $1$ sont les nombres complexes
$$w_k = \exp\left( \frac{2ik\pi}{n} \right) = \cos\left( \frac{2k\pi}{n} \right) + i \sin \left( \frac{2k\pi}{n} \right)$$ pour $k \in \{0, 1, \ldots, n-1\}$. Notez que la valeur de $w_k$ dépend bel et bien de $n$, même si la notation ne l'indique pas ! Pour $k = 0$, on retrouve $w_0 = 1$, alors que quand $n$ est pair, on retrouve $w_{\frac{n}{2}} = e^{i \pi} = -1$ ce qui est logique puisque $-1$ est bien une racine $n$-ème de $1$ lorsque $n$ est pair. L'ensemble des racines $n$-èmes de l'unité est donc l'ensemble des sommets du $n$-gone centré en l'origine et ayant $1$ pour sommet. Sur la figure suivante, les racines $6$-èmes de l'unité sont représentées.
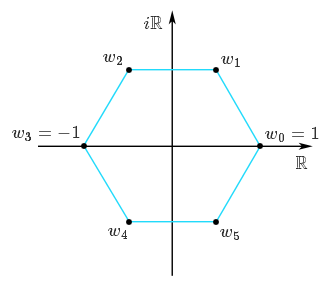
Les racines de l'unité sont intéressantes car, dès que l'on connait une racine $n$-ème d'un complexe non nul $c$, on peut trouver toutes les autres en la multipliant par les différentes racines $n$-èmes de $1$.
$$\left(r \cdot e^{i \theta} \right)^n = r^n \cdot e^{in\theta}.$$ Réciproquement, cela permet d'extraire les racines $n$-èmes d'un nombre complexe très facilement, alors que nous avons vu précédemment qu'extraire une racine carrée était déjà fastidieux sous la forme usuelle. Pour le voir, considérons un nombre complexe non nul $c = r\cdot e^{i \theta}$ et cherchons quelles sont ses racines $n$-èmes. Un nombre $z = s \cdot e^{i \varphi}$ (de module $s$ et d'argument $\varphi$) est racine $n$-ème de $c$ si et seulement si sa $n$-ème puissance vaut $c$, c'est-à-dire si
$$s^n \cdot e^{in\varphi} = r \cdot e^{i\theta}.$$ Les modules doivent être égaux donc $s = \sqrt[n]{r}$, et les arguments aussi d'où $n\varphi = \theta$. Cette dernière égalité n'est cependant pas tout à fait correcte. En effet, nous avons mentionné que nous considérions des angles comme égaux dès qu'ils étaient égaux à un multiple de $2\pi$ près. Il ne faut donc pas avoir $n\varphi = \theta$, mais plutôt $n \varphi = \theta + 2k \pi$ pour un certain $k \in \mathbb{Z}$. Les racines $n$-èmes de $c = r \cdot e^{i \theta}$ sont donc les nombres complexes de la forme (on note $\exp$ au lieu de $e$ pour des raisons pratiques)
$$z_k = \sqrt[n]{r} \cdot \exp\left(i\left(\frac{\theta}{n} + \frac{2k\pi}{n}\right)\right)$$ avec $k \in \mathbb{Z}$. En fait, on voit aisément qu'il n'y a pas une infinité de racines mais exactement $n$, car la valeur de cette expression pour $k = n$ est la même que celle pour $k = 0$. Tout nombre complexe non nul possède donc exactement $n$ racines $n$-èmes, en prenant par exemple $z_0, \ldots, z_{n-1}$.
Interprétation géométrique
Regardons finalement comment construire les différentes racines $n$-èmes d'un nombre complexe sur le plan complexe. Si on considère la racine obtenue avec $k = 0$, celle-ci s'obtient simplement en prenant la racine $n$-ème du module et en divisant l'argument par $n$. Ensuite, les autres racines s'obtiennent simplement en augmentant l'argument d'un multiple de $\displaystyle \frac{2\pi}{n}$, c'est-à-dire en effectuant une rotation de cet angle. Les racines $n$-èmes d'un complexe sont donc toujours les sommets d'un $n$-gône régulier.En particulier, les racines $n$-èmes de $1$ sont les nombres complexes
$$w_k = \exp\left( \frac{2ik\pi}{n} \right) = \cos\left( \frac{2k\pi}{n} \right) + i \sin \left( \frac{2k\pi}{n} \right)$$ pour $k \in \{0, 1, \ldots, n-1\}$. Notez que la valeur de $w_k$ dépend bel et bien de $n$, même si la notation ne l'indique pas ! Pour $k = 0$, on retrouve $w_0 = 1$, alors que quand $n$ est pair, on retrouve $w_{\frac{n}{2}} = e^{i \pi} = -1$ ce qui est logique puisque $-1$ est bien une racine $n$-ème de $1$ lorsque $n$ est pair. L'ensemble des racines $n$-èmes de l'unité est donc l'ensemble des sommets du $n$-gone centré en l'origine et ayant $1$ pour sommet. Sur la figure suivante, les racines $6$-èmes de l'unité sont représentées.

Les racines de l'unité sont intéressantes car, dès que l'on connait une racine $n$-ème d'un complexe non nul $c$, on peut trouver toutes les autres en la multipliant par les différentes racines $n$-èmes de $1$.