Polynômes
Racines
Définition de racine
Lorsqu'on a un polynôme de $K[x]$ de la forme$$P(x) = c_n x^n + c_{n-1}x^{n-1}+\ldots + c_1 x + c_0,$$ on peut bien sûr l'évaluer en un élément $a \in K$, en prenant simplement
$$P(a) = c_n a^n + c_{n-1}a^{n-1}+\ldots + c_1 a + c_0.$$ On peut alors définir une racine du polynôme $P$ comme étant un nombre $a \in K$ tel que $P(a) = 0$. On a alors le résultat suivant.
Lemme
Soit $P \in K[x]$ un polynôme (où $K$ est un corps commutatif). Si $a \in K$, alors le reste de la division euclidienne de $P$ par $x-a$ est $P(a)$. En particulier, $a$ est une racine de $P$ si et seulement si $P$ est divisible par $x-a$.
Démonstration
Lorsqu'on effectue la division euclidienne de $P$ par $x-a$, on obtient un reste de degré inférieur à $1$, c'est-à-dire une constante. On a donc
$$P = (x-a) \cdot Q + r,$$ pour un polynôme $Q$ et un élément $r \in K$. En évaluant les deux membres en $x = a$, on voit directement que
$$P(a) = r.$$ De plus, $a$ est une racine de $P$ si et seulement si $0 = P(a) = r$, c'est-à-dire si et seulement si $P$ est divisible par $x-a$.
$$P = (x-a) \cdot Q + r,$$ pour un polynôme $Q$ et un élément $r \in K$. En évaluant les deux membres en $x = a$, on voit directement que
$$P(a) = r.$$ De plus, $a$ est une racine de $P$ si et seulement si $0 = P(a) = r$, c'est-à-dire si et seulement si $P$ est divisible par $x-a$.
Lorsque l'on a une racine $a$ de $P$, on peut donc diviser $P$ par $x-a$ sans qu'il n'y ait de reste. On peut bien sûr utiliser la méthode de la "potence" pour effectuer cette division, mais il existe en fait une méthode plus pratique via le schéma de Horner. Pour diviser le polynôme
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ par $x-a$, on construit le schéma suivant :
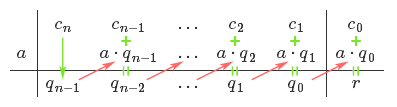
On abaisse d'abord $c_n$ et pose $q_{n-1} = c_n$. On multiplie ensuite $q_{n-1}$ par $a$ et écrit le résultat en dessous de $c_{n-1}$. On pose alors $q_{n-2} = c_{n-1} + a\cdot q_{n-1}$, et continue ce processus jusqu'au bout du tableau. À la fin, on note $r$ le dernier élément obtenu et celui-ci sera toujours égal au reste de la division, c'est-à-dire à $P(a)$ (dans le cas contraire, c'est qu'une erreur a été commise). Le polynôme quotient est quand à lui donné par
$$Q(x) = q_{n-1} x^{n-1} + \ldots + q_1 x + q_0.$$ Montrer que cette méthode donne bien le bon résultat est un simple exercice.
Racine multiple
Le polynôme $P(x) = x^3 - 4x^2 + 4x = x(x-2)^2$ a évidemment $2$ pour racine. Par ailleurs, on voit que $x-2$ divise bien $P$, conformément au résultat précédent. Intuitivement, il semble qu'on ait même un peu mieux qu'une racine, puisque $x-2$ divise "deux fois" $P$, au sens où $(x-2)^2$ le divise. Dans un tel cas, on dit en fait que $2$ est une racine double du polynôme, ou encore qu'il s'agit d'une racine de multiplicité $2$.De manière générale, on définit la multiplicité d'une racine $a$ de $P$ comme étant le plus grand naturel $m$ tel que $(x-a)^m$ divise $P$. Un nombre qui n'est pas une racine de $P$ peut donc être considéré comme une racine de multiplicité nulle.
Pour le résultat suivant, on a besoin de la notion de polynôme dérivé. Pour ceux qui connaissent les dérivées, il s'agit simplement de la dérivée du polynôme. Cela dit, on peut simplement définir le polynôme dérivé de
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ comme étant le polynôme
$$P'(x) = nc_n x^{n-1} + (n-1) c_{n-1} x^{n-2} + \ldots + c_1$$ (pour chaque terme, on "abaisse" l'exposant de $x$ en le mettant devant le coefficient et on diminue cet exposant de $1$). On peut itérer la dérivée et on parle alors de dérivée seconde $P''$ lorsque l'on dérive $P$ deux fois consécutivement, tout comme la dérivée $k$-ème notée $P^{(k)}$ qui est le résultat de $k$ dérivations successives.
Proposition
Soit $P \in K[x]$ un polynôme. Un élément $a \in K$ est une racine de $P$ de multiplicité $m \in \mathbb{N}$ si et seulement si
$$P(a) = P'(a) = \ldots = P^{(m-1)}(a) = 0$$ mais $P^{(m)}(a) \neq 0$.
$$P(a) = P'(a) = \ldots = P^{(m-1)}(a) = 0$$ mais $P^{(m)}(a) \neq 0$.
Nous ne démontrons pas ce résultat mais l'illustrons sur l'exemple précédemment donné $P(x) = x^3 - 4x^2 + 4x$. Calculons d'abord ses dérivées successives :
$$P'(x) = 3x^2 - 8x + 4,$$ $$P''(x) = 6x - 8,$$ $$P^{(3)}(x) = 6,$$ $$P^{(4)}(x) = 0.$$ Évaluons alors $P$ et ses différentes dérivées en $a = 2$ :
$$P(2) = 2^3 - 4\cdot 2^2+4\cdot 2 = 8-16+8=0,$$ $$P'(2) = 3\cdot 2^2 - 8 \cdot 2 + 4 = 12 - 16 + 4 = 0,$$ $$P''(2) = 6\cdot 2 - 8 = 12 - 8 = 4.$$ Par le résultat précédent, $2$ est donc une racine de multiplicité $2$ de $P$, ce que nous avions bien observé par définition de multiplicité puisque $P(x) = x(x-2)^2$.