Polynômes (suite)
Formule de Taylor
Lorsqu'on est en présence d'un polynôme $P$ de $A[x]$ et qu'un certain $a \in A$ est une valeur que l'on désire privilégier, il peut être utile de ne plus écrire notre polynôme sous la forme usuelle
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0,$$ mais plutôt sous une forme du type
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ La formule de Taylor nous donne en fait une façon d'exprimer les coefficients $c'_i$ à partir des valeurs en $a$ des différents polynômes dérivés de $P$.
Remarquons que $\displaystyle \frac{P^{(n)}(a)}{n!}$ est toujours égal à $c_n$, le coefficient dominant de $P$, d'où $c'_n = c_n$ ce qui est parfaitement logique.
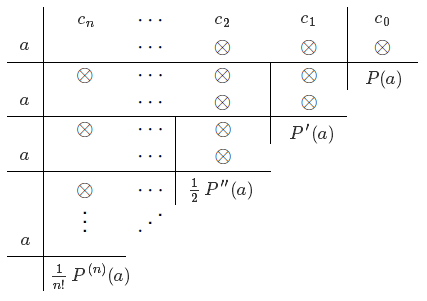
Il est en fait possible d'obtenir les valeurs des coefficients $c'_k$ en itérant le schéma de Horner. En effet, nous avons vu qu'en utilisant celui-ci pour diviser $P$ par $(x-a)$, la dernière valeur du tableau obtenue sera le reste de la division, à savoir $P(a)$. On peut alors recommencer en divisant le quotient obtenu $Q$ par $(x-a)$ et le reste obtenu sera exactement $c'_1 = P'(a)$. On continue ainsi de suite, et le reste à chaque étape sera exactement le coefficient suivant de la formule de Taylor.
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0,$$ mais plutôt sous une forme du type
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ La formule de Taylor nous donne en fait une façon d'exprimer les coefficients $c'_i$ à partir des valeurs en $a$ des différents polynômes dérivés de $P$.
Formule de Taylor
Soit $P \in A[x]$ un polynôme de degré $n$, et $a \in A$. On a
$$P(x) = \frac{P^{(n)}(a)}{n!} (x-a)^n + \frac{P^{(n-1)}(a)}{(n-1)!} (x-a)^{n-1} + \ldots + P'(a) (x-a) + P(a).$$
$$P(x) = \frac{P^{(n)}(a)}{n!} (x-a)^n + \frac{P^{(n-1)}(a)}{(n-1)!} (x-a)^{n-1} + \ldots + P'(a) (x-a) + P(a).$$
Remarquons que $\displaystyle \frac{P^{(n)}(a)}{n!}$ est toujours égal à $c_n$, le coefficient dominant de $P$, d'où $c'_n = c_n$ ce qui est parfaitement logique.
Démonstration
On peut facilement se convaincre qu'il existe effectivement des coefficients $c'_i$ tels que
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ En effet, on prend $c'_n = c_n$, puis on choisit $c'_{n-1}$ de sorte que le coefficient de $x^{n-1}$ soit correct, puis $c'_{n-2}$, et ainsi de suite jusque $c'_0$. Il reste donc uniquement à exprimer chaque $c'_i$ en fonction des polynômes dérivés. Pour cela, on commence à évaluer $P$ en $a$ et on remarque que
$$P(a) = c'_n (a-a)^n + c'_{n-1} (a-a)^{n-1} + \ldots + c'_1 (a-a) + c'_0,$$ ce qui montre que $c'_0 = P(a)$. On calcule ensuite
$$P'(x) = nc'_n (x-a)^{n-1} + (n-1)c'_{n-1} (x-a)^{n-2} + \ldots + 2c'_2(x-a)+ c'_1,$$ et en évaluant $P'$ en $a$ on voit que $P'(a) = c'_1$. En continuant de la sorte, on verra que $P''(a) = 2c'_2$, puis $P^{(3)}(a) = 3\cdot2 \cdot c'_3$, et ainsi de suite. On obtient en fait à chaque étape la formule attendue
$$c'_k = \frac{P^{(k)}(a)}{k!}.$$
$$P(x) = c'_n (x-a)^n + c'_{n-1} (x-a)^{n-1} + \ldots + c'_1 (x-a) + c'_0.$$ En effet, on prend $c'_n = c_n$, puis on choisit $c'_{n-1}$ de sorte que le coefficient de $x^{n-1}$ soit correct, puis $c'_{n-2}$, et ainsi de suite jusque $c'_0$. Il reste donc uniquement à exprimer chaque $c'_i$ en fonction des polynômes dérivés. Pour cela, on commence à évaluer $P$ en $a$ et on remarque que
$$P(a) = c'_n (a-a)^n + c'_{n-1} (a-a)^{n-1} + \ldots + c'_1 (a-a) + c'_0,$$ ce qui montre que $c'_0 = P(a)$. On calcule ensuite
$$P'(x) = nc'_n (x-a)^{n-1} + (n-1)c'_{n-1} (x-a)^{n-2} + \ldots + 2c'_2(x-a)+ c'_1,$$ et en évaluant $P'$ en $a$ on voit que $P'(a) = c'_1$. En continuant de la sorte, on verra que $P''(a) = 2c'_2$, puis $P^{(3)}(a) = 3\cdot2 \cdot c'_3$, et ainsi de suite. On obtient en fait à chaque étape la formule attendue
$$c'_k = \frac{P^{(k)}(a)}{k!}.$$
Il est en fait possible d'obtenir les valeurs des coefficients $c'_k$ en itérant le schéma de Horner. En effet, nous avons vu qu'en utilisant celui-ci pour diviser $P$ par $(x-a)$, la dernière valeur du tableau obtenue sera le reste de la division, à savoir $P(a)$. On peut alors recommencer en divisant le quotient obtenu $Q$ par $(x-a)$ et le reste obtenu sera exactement $c'_1 = P'(a)$. On continue ainsi de suite, et le reste à chaque étape sera exactement le coefficient suivant de la formule de Taylor.
