Solutions non classiques
BxMO 2014
Voici le problème 4 de la BxMO (Benelux Mathematical Olympiad) 2014 :
Lors de la compétition, aucun participant n'a résolu ce problème. Celui-ci n'était pourtant pas insurmontable, et ces mauvais résultats sont certainement dus au manque de temps (puisqu'il y avait trois autres problèmes à résoudre en même temps). Ce problème possède bien sûr une solution classique (et c'est un bon exercice de la chercher), mais il était en fait également possible de le résoudre par géométrie analytique. La présence d'un carré et l'absence de cercles (qui compliquent souvent tout) est en effet un bon indicateur du fait qu'il devrait être possible d'utiliser la géométrie analytique.
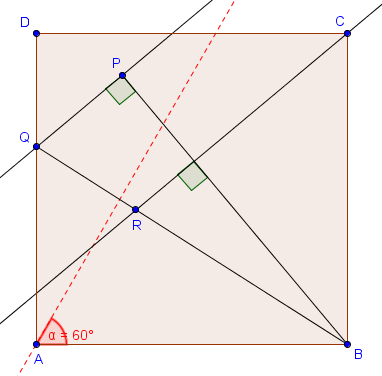
Problème (BxMO 2014, P4)
Soit $ABCD$ un carré. On considère un point variable $P$ à l’intérieur du carré tel que $\widehat{BAP} ≥ 60^\circ$. Soit $Q$ l’intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. Soit $R$ l’intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$.
(a) Prouver que $|BP| \geq |BR|$.
(b) Pour quel(s) point(s) $P$ l’inégalité en (a) devient-elle une égalité ?
(a) Prouver que $|BP| \geq |BR|$.
(b) Pour quel(s) point(s) $P$ l’inégalité en (a) devient-elle une égalité ?
Lors de la compétition, aucun participant n'a résolu ce problème. Celui-ci n'était pourtant pas insurmontable, et ces mauvais résultats sont certainement dus au manque de temps (puisqu'il y avait trois autres problèmes à résoudre en même temps). Ce problème possède bien sûr une solution classique (et c'est un bon exercice de la chercher), mais il était en fait également possible de le résoudre par géométrie analytique. La présence d'un carré et l'absence de cercles (qui compliquent souvent tout) est en effet un bon indicateur du fait qu'il devrait être possible d'utiliser la géométrie analytique.

Solution analytique
Naturellement, posons l'origine de notre repère comme étant $A$, l'axe des abscisses pointant vers $B$ et l'axe des ordonnées vers $D$. On peut aussi supposer que le carré est de côté $1$. On a alors $\boxed{A \ (0,0)}$, $\boxed{B \ (1, 0)}$, $\boxed{C \ (1,1)}$ et $\boxed{D \ (0,1)}$.
Notons ensuite $\boxed{P \ (p_1,p_2)}$ avec $0 < p_1, p_2 < 1$. Essayons de traduire $\widehat{BAP} \geq 60^\circ$ en équations. La droite passant par $A$ et faisant un angle de $60^\circ$ avec $AB$ a pour équation $y = \sqrt{3} \cdot x$ (comme on peut s'en convaincre de différentes façons), et $P$ doit se situer au dessus de cette droite, donc on a $\boxed{p_2 \geq \sqrt{3} \cdot p_1}$.
Le point $Q$ est maintenant l'intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. La pente de la droite $BP$ est $(p_1-1, p_2)$, et donc la pente d'une perpendiculaire à $BP$ est $(p_2, 1-p_1)$ (voir formules dans le point théorique précédent). L'équation de la droite de pente $(p_2, 1-p_1)$ passant par $P \ (p_1, p_2)$ est alors
$$\frac{x-p_1}{p_2} = \frac{y-p_2}{1-p_1}. \quad (1)$$ Nous cherchons l'intersection de cette droite avec la droite $AD$, qui a la simple équation $x = 0$. Il suffit donc de poser $x = 0$ dans $(1)$ et de trouver $y$. On obtient $y = p_2 + \frac{(p_1-1)p_1}{p_2} = \frac{p_2^2 + p_1^2 - p_1}{p_2}$. Donc les coordonnées de $Q$ sont $\boxed{Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)}$.
Le point $R$ est l'intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$. Nous avons déjà dit qu'une perpendiculaire à $BP$ avait pour pente $(p_2, 1-p_1)$, et la perpendiculaire à $BP$ passant par $C \ (1,1)$ a donc pour équation :
$$\frac{x-1}{p_2} = \frac{y-1}{1-p_1}$$ $$\Leftrightarrow (1-p_1)(x-1) = p_2(y-1). \quad (2)$$ D'autre part, la droite $BQ$ passe par $B \ (1,0)$ et $Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$, donc sa pente est $\left(-1, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$ et son équation est
$$\frac{x-1}{-1} = \frac{y-0}{\frac{p_2^2 + p_1^2 - p_1}{p_2}}. \quad (3)$$ Il reste à remettre $(2)$ et $(3)$ ensemble pour trouver les coordonnées de $R$. Par $(3)$, on voit que $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x)$. En remplaçant $y$ par cette expression dans $(2)$, on trouve alors que
$$(1-p_1)(x-1) = p_2\left(\frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) - 1\right)$$ $$\Leftrightarrow (1-p_1)x + p_1 - 1 = p_2^2+p_1^2-p_1-p_2 - (p_2^2+p_1^2-p_1)\cdot x$$ $$\Leftrightarrow (p_2^2+p_1^2-2p_1+1)\cdot x = p_2^2-p_2+p_1^2-2p_1+1$$ $$\Leftrightarrow (p_2^2 + (p_1-1)^2)\cdot x = p_2^2-p_2+ (p_1-1)^2$$ $$\Leftrightarrow x = \frac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}$$ On peut alors trouver $1-x = \frac{p_2}{p_2^2 + (p_1-1)^2}$ et donc $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) = \frac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2}$. Les coordonnées de $R$ sont donc $\boxed{R \ \left( \dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}, \ \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2 + (p_1-1)^2} \right)}$, et heureusement il n'y a plus de coordonnées à calculer...
Nous cherchons à montrer que $|BP| \geq |BR|$, ce qui revient à dire que $|BP|^2 \geq |BR|^2$. D'une part, on a $|BP|^2 = (p_1-1)^2 + p_2^2$, et d'autre part, on a
$$\begin{align}
|BR|^2 &= \left(\dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2} - 1\right)^2 + \left( \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2} \right)^2\\
&= \left(\dfrac{-p_2}{p_2^2+ (p_1-1)^2}\right)^2 + \left( 1+\dfrac{p_1-1}{p_2^2 + (p_1-1)^2} \right)^2\\
&= \frac{p_2^2}{(p_2^2+ (p_1-1)^2)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} + \frac{(p_1-1)^2}{(p_2^2+ (p_1-1)^2)^2}\\
&= \frac{1}{p_2^2+ (p_1-1)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} \\
&= \frac{2p_1-1+p_2^2+(p_1-1)^2}{p_2^2+ (p_1-1)^2} \\
&= \frac{p_2^2+p_1^2}{p_2^2+ (p_1-1)^2}
\end{align}$$ L'inégalité $|BP|^2 \geq |BR|^2$ se réécrit donc
$$(p_2^2+(p_1-1)^2)^2 \geq p_2^2+p_1^2, \quad (4)$$ dont on remarque qu'il s'agit juste de
$$|BP|^2 \geq |AP|.$$ Il serait possible de continuer avec $p_1$ et $p_2$ et de montrer que l'inégalité est vraie en utilisant que $p_2 \geq \sqrt{3} \cdot p_1$, mais il est en fait plus facile d'essayer de prouver que $|BP|^2 \geq |AP|$ plus géométriquement. En effet, on sait par la loi des cosinus dans le triangle $ABP$ que $|BP|^2 = |AB|^2+|AP|^2 - 2|AB||AP|\cos\widehat{BAP} = 1 + |AP|^2 - 2 |AP|\cos \widehat{BAP}$, et l'inégalité $|BP|^2 \geq |AP|$ peut donc se réécrire comme
$$1 + |AP|^2 - 2 |AP| \cos \widehat{BAP} \geq |AP|$$ $$\Leftrightarrow |AP|^2 - (2 \cos \widehat{BAP}+1) \cdot |AP| + 1 \geq 0.$$ Il s'agit d'une équation du second degré en $|AP|$, dont le discriminant est $(2 \cos \widehat{BAP}+1)^2 - 4$. Comme $60^\circ \leq \widehat{BAP} < 90^\circ$, on a $0 < \cos \widehat{BAP} \leq \frac 12$ et le discriminant est toujours négatif ou nul. Puisque le coefficient de $|AP|^2$ est positif, on en déduit que ce polynôme est toujours positif et nous avons donc prouvé (a). La seule façon d'avoir l'égalité est que le discriminant soit nul, i.e. que $\widehat{BAP} = 60^\circ$, et que $|AP|$ soit l'unique racine du polynôme, qui est alors $|AP| = 1$. Le point $P$ satisfaisant ces deux conditions est le point à l'intérieur de $ABCD$ tel que $ABP$ est équilatéral, ce qui répond au point (b).
Notons ensuite $\boxed{P \ (p_1,p_2)}$ avec $0 < p_1, p_2 < 1$. Essayons de traduire $\widehat{BAP} \geq 60^\circ$ en équations. La droite passant par $A$ et faisant un angle de $60^\circ$ avec $AB$ a pour équation $y = \sqrt{3} \cdot x$ (comme on peut s'en convaincre de différentes façons), et $P$ doit se situer au dessus de cette droite, donc on a $\boxed{p_2 \geq \sqrt{3} \cdot p_1}$.
Le point $Q$ est maintenant l'intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. La pente de la droite $BP$ est $(p_1-1, p_2)$, et donc la pente d'une perpendiculaire à $BP$ est $(p_2, 1-p_1)$ (voir formules dans le point théorique précédent). L'équation de la droite de pente $(p_2, 1-p_1)$ passant par $P \ (p_1, p_2)$ est alors
$$\frac{x-p_1}{p_2} = \frac{y-p_2}{1-p_1}. \quad (1)$$ Nous cherchons l'intersection de cette droite avec la droite $AD$, qui a la simple équation $x = 0$. Il suffit donc de poser $x = 0$ dans $(1)$ et de trouver $y$. On obtient $y = p_2 + \frac{(p_1-1)p_1}{p_2} = \frac{p_2^2 + p_1^2 - p_1}{p_2}$. Donc les coordonnées de $Q$ sont $\boxed{Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)}$.
Le point $R$ est l'intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$. Nous avons déjà dit qu'une perpendiculaire à $BP$ avait pour pente $(p_2, 1-p_1)$, et la perpendiculaire à $BP$ passant par $C \ (1,1)$ a donc pour équation :
$$\frac{x-1}{p_2} = \frac{y-1}{1-p_1}$$ $$\Leftrightarrow (1-p_1)(x-1) = p_2(y-1). \quad (2)$$ D'autre part, la droite $BQ$ passe par $B \ (1,0)$ et $Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$, donc sa pente est $\left(-1, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$ et son équation est
$$\frac{x-1}{-1} = \frac{y-0}{\frac{p_2^2 + p_1^2 - p_1}{p_2}}. \quad (3)$$ Il reste à remettre $(2)$ et $(3)$ ensemble pour trouver les coordonnées de $R$. Par $(3)$, on voit que $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x)$. En remplaçant $y$ par cette expression dans $(2)$, on trouve alors que
$$(1-p_1)(x-1) = p_2\left(\frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) - 1\right)$$ $$\Leftrightarrow (1-p_1)x + p_1 - 1 = p_2^2+p_1^2-p_1-p_2 - (p_2^2+p_1^2-p_1)\cdot x$$ $$\Leftrightarrow (p_2^2+p_1^2-2p_1+1)\cdot x = p_2^2-p_2+p_1^2-2p_1+1$$ $$\Leftrightarrow (p_2^2 + (p_1-1)^2)\cdot x = p_2^2-p_2+ (p_1-1)^2$$ $$\Leftrightarrow x = \frac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}$$ On peut alors trouver $1-x = \frac{p_2}{p_2^2 + (p_1-1)^2}$ et donc $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) = \frac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2}$. Les coordonnées de $R$ sont donc $\boxed{R \ \left( \dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}, \ \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2 + (p_1-1)^2} \right)}$, et heureusement il n'y a plus de coordonnées à calculer...
Nous cherchons à montrer que $|BP| \geq |BR|$, ce qui revient à dire que $|BP|^2 \geq |BR|^2$. D'une part, on a $|BP|^2 = (p_1-1)^2 + p_2^2$, et d'autre part, on a
$$\begin{align}
|BR|^2 &= \left(\dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2} - 1\right)^2 + \left( \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2} \right)^2\\
&= \left(\dfrac{-p_2}{p_2^2+ (p_1-1)^2}\right)^2 + \left( 1+\dfrac{p_1-1}{p_2^2 + (p_1-1)^2} \right)^2\\
&= \frac{p_2^2}{(p_2^2+ (p_1-1)^2)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} + \frac{(p_1-1)^2}{(p_2^2+ (p_1-1)^2)^2}\\
&= \frac{1}{p_2^2+ (p_1-1)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} \\
&= \frac{2p_1-1+p_2^2+(p_1-1)^2}{p_2^2+ (p_1-1)^2} \\
&= \frac{p_2^2+p_1^2}{p_2^2+ (p_1-1)^2}
\end{align}$$ L'inégalité $|BP|^2 \geq |BR|^2$ se réécrit donc
$$(p_2^2+(p_1-1)^2)^2 \geq p_2^2+p_1^2, \quad (4)$$ dont on remarque qu'il s'agit juste de
$$|BP|^2 \geq |AP|.$$ Il serait possible de continuer avec $p_1$ et $p_2$ et de montrer que l'inégalité est vraie en utilisant que $p_2 \geq \sqrt{3} \cdot p_1$, mais il est en fait plus facile d'essayer de prouver que $|BP|^2 \geq |AP|$ plus géométriquement. En effet, on sait par la loi des cosinus dans le triangle $ABP$ que $|BP|^2 = |AB|^2+|AP|^2 - 2|AB||AP|\cos\widehat{BAP} = 1 + |AP|^2 - 2 |AP|\cos \widehat{BAP}$, et l'inégalité $|BP|^2 \geq |AP|$ peut donc se réécrire comme
$$1 + |AP|^2 - 2 |AP| \cos \widehat{BAP} \geq |AP|$$ $$\Leftrightarrow |AP|^2 - (2 \cos \widehat{BAP}+1) \cdot |AP| + 1 \geq 0.$$ Il s'agit d'une équation du second degré en $|AP|$, dont le discriminant est $(2 \cos \widehat{BAP}+1)^2 - 4$. Comme $60^\circ \leq \widehat{BAP} < 90^\circ$, on a $0 < \cos \widehat{BAP} \leq \frac 12$ et le discriminant est toujours négatif ou nul. Puisque le coefficient de $|AP|^2$ est positif, on en déduit que ce polynôme est toujours positif et nous avons donc prouvé (a). La seule façon d'avoir l'égalité est que le discriminant soit nul, i.e. que $\widehat{BAP} = 60^\circ$, et que $|AP|$ soit l'unique racine du polynôme, qui est alors $|AP| = 1$. Le point $P$ satisfaisant ces deux conditions est le point à l'intérieur de $ABCD$ tel que $ABP$ est équilatéral, ce qui répond au point (b).
Remarque importante
On voit sur cet exemple que les calculs deviennent vite laborieux en géométrie analytique. La moindre erreur dans le calcul d'une coordonnée est d'ailleurs fatale, et il faut donc être très concentré pour envisager un tel développement. Puisque ce genre de solution peut vite prendre beaucoup de temps, il est primordial en compétition de ne pas se lancer dans des solutions analytiques à tout bout de champ. Il serait dommage de passer tout son temps sur une telle solution en ignorant les autres problèmes, d'autant plus qu'elle peut ne pas aboutir. Il faut aussi noter que les solutions analytiques sont souvent mal payées en points lors de compétitions. Si une solution complète au problème est donnée, comme ci-dessus, alors elle sera gratifiée d'un score de $7/7$, mais si on arrive par exemple à l'inégalité $(4)$ sans parvenir à conclure alors on n'obtiendra que très peu de points (pas plus de $2/7$, et cela peut être encore plus sévère).