Transformations du plan
Isométries
Une transformation du plan est, comme son nom l'indique, une transformation particulière que l'on peut appliquer aux objets dans le plan. Il existe plusieurs types de transformations du plan, et nous nous penchons d'abord sur les plus connues : les rotations, translations et symétries orthogonales. Dans cette section, tous les angles seront orientés.
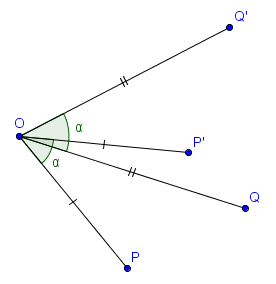
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par rotation de centre $O$ et d'angle $\alpha = 45^\circ$. Pour trouver $P'$ et $Q'$, on voit qu'il suffit de faire tourner $P$ et $Q$ autour de $O$ avec un angle de $45^\circ$.
Les rotations ont une propriété fondamentale : ce sont des isométries.
Il existe un type de rotation particulier : les symétries centrales. Étant donné un point $O$, la symétrie centrale de centre $O$ est un autre nom pour la rotation de centre $O$ et d'angle $\pi$ (c'est-à-dire $180^\circ$). La symétrie centrale est plus facile à définir : l'image du point $P$ par la symétrie centrale de centre $O$ est juste le point $P'$ tel que $O$ soit le milieu de $[PP']$. Le point $P'$ est alors le symétrique de $P$ par rapport à $O$.
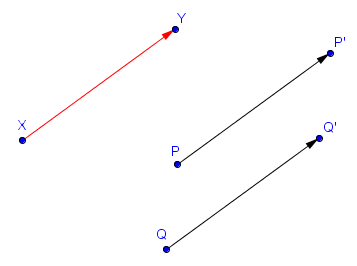
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la translation appliquant $X$ sur $Y$.
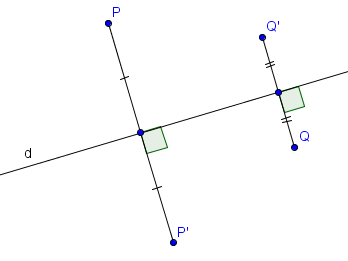
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la symétrie orthogonale d'axe $d$.
Certaines isométries ont des propriétés supplémentaires, qui découlent généralement de leur définition. On a par exemple que l'image d'une droite par une translation ou par une symétrie centrale est une droite qui lui est parallèle.
Rotations
Étant donné un point $O$ du plan et un angle $\alpha \in [0, 2\pi[$ (en radians), on peut considérer la rotation de centre $O$ et d'angle $\alpha$. Intuitivement, il s'agit de faire tourner le plan autour de $O$, d'un angle $\alpha$. Plus précisément et par définition, l'image d'un point $P$ par la rotation de centre $O$ et d'angle $\alpha$ est l'unique point $P'$ tel que $|OP'| = |OP|$ et $\widehat{POP'} = \alpha$ (en angles orientés, de sorte qu'il n'y ait qu'un seul tel point et non deux).Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par rotation de centre $O$ et d'angle $\alpha = 45^\circ$. Pour trouver $P'$ et $Q'$, on voit qu'il suffit de faire tourner $P$ et $Q$ autour de $O$ avec un angle de $45^\circ$.

Les rotations ont une propriété fondamentale : ce sont des isométries.
Propriété
Une rotation est une isométrie, c'est-à-dire une transformation qui préserve les longueurs. Autrement dit, si $P'$ et $Q'$ sont les images de deux points $P$ et $Q$ par une même rotation, alors $|P'Q'| = |PQ|$.
Il existe un type de rotation particulier : les symétries centrales. Étant donné un point $O$, la symétrie centrale de centre $O$ est un autre nom pour la rotation de centre $O$ et d'angle $\pi$ (c'est-à-dire $180^\circ$). La symétrie centrale est plus facile à définir : l'image du point $P$ par la symétrie centrale de centre $O$ est juste le point $P'$ tel que $O$ soit le milieu de $[PP']$. Le point $P'$ est alors le symétrique de $P$ par rapport à $O$.
Translations
Étant donnés deux points $X$ et $Y$ du plan, on peut considérer la translation appliquant $X$ sur $Y$. Intuitivement, il s'agit de faire glisser le plan de sorte à ce que $X$ devienne $Y$. Plus précisément, l'image d'un point $P$ par la translation appliquant $X$ sur $Y$ est l'unique point $P'$ tel que $\vec{PP'} = \vec{XY}$. Pour ceux ne connaissant pas la notion de vecteurs, cela signifie simplement que la flèche reliant $P$ à $P'$ doit être exactement la même (c'est-à-dire de même longueur, direction et sens) que celle reliant $X$ à $Y$.Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la translation appliquant $X$ sur $Y$.

Propriété
Une translation est une isométrie.
Symétries orthogonales
Étant donnée une droite $d$ du plan, on peut considérer la symétrie orthogonale d'axe $d$. Intuitivement, on peut penser à $d$ comme à un miroir. Par définition, l'image d'un point $P$ par la symétrie orthogonale d'axe $d$ est l'unique point $P'$ tel que $PP'$ est perpendiculaire à $d$ et le milieu de $[PP']$ se trouve sur $d$. On dit que $P'$ est le symétrique de $P$ par rapport à l'axe $d$.Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la symétrie orthogonale d'axe $d$.

Propriété
Une symétrie orthogonale est une isométrie. De plus, si $P'$ est l'image de $P$ par une symétrie orthogonale, alors $P$ est l'image de $P'$ par cette même symétrie.
Propriétés
Les rotations, translations et symétries orthogonales partagent un grand nombre de propriétés, du fait que ce sont des isométries.Propriétés des isométries
Les isométries conservent :
- la longueur des segments (par définition d'isométrie) : $|P'Q'| = |PQ|$;
- l'amplitude des angles : $\widehat{P'Q'R'} = \widehat{PQR}$;
- l'alignement des points : si $P$, $Q$ et $R$ sont alignés, alors $P'$, $Q'$ et $R'$ sont alignés (c'est un cas particulier du point 2);
- le parallélisme des droites : si $PQ$ et $RS$ sont parallèles, alors $P'Q'$ et $R'S'$ sont parallèles;
- la perpendicularité des droites : si $PQ$ et $RS$ sont perpendiculaires, alors $P'Q'$ et $R'S'$ sont perpendiculaires (cas particulier du point 2);
- le milieu d'un segment : si $M$ est le milieu de $[PQ]$, alors $M'$ est le milieu de $[P'Q']$ (conséquence des points 1 et 3);
- le périmètre et l'aire des figures.
- ...
Certaines isométries ont des propriétés supplémentaires, qui découlent généralement de leur définition. On a par exemple que l'image d'une droite par une translation ou par une symétrie centrale est une droite qui lui est parallèle.
Classification des isométries
Comme vu plus haut, les rotations, translations et symétries orthogonales sont des isométries. En fait, il s'agit des seules isométries du plan (à une petite exception près) !Classification des isométries du plan
Soit $f$ une isométrie du plan, c'est-à-dire une fonction $f : \mathbb{R}^2 \to \mathbb{R}^2$ qui est une bijection et qui préserve les longueurs.
- Si $f$ a trois points fixes non-alignés, alors $f$ est l'identité.
- Si $f$ n'est pas l'identité et a au moins deux points fixes $A$ et $B$, alors $f$ est la symétrie orthogonale d'axe $AB$.
- Si $f$ a un unique point fixe $A$, alors $f$ est une rotation de centre $A$.
- Si $f$ n'a pas de point fixe, alors:
- soit $f$ est une translation,
- soit $f$ est la composée d'une symétrie orthogonale et d'une translation de vecteur parallèle à l'axe de symétrie.