Transformations du plan
Utilisation
Lorsque l'on est en présence d'un problème de géométrie, appliquer à tout le plan une transformation du type rotation, translation, symétrie orthogonale ou homothétie n'a pas réellement d'intérêt. En effet, une telle transformation revient juste à faire tourner la figure, la bouger ou zoomer dessus, mais cela ne va bien sûr aucunement aider à résoudre le problème.
Pour illustrer la manière dont une telle transformation peut se révéler utile, considérons le problème suivant.
Il aurait bien sûr été possible de montrer, sans utiliser de rotation, que les deux triangles $BDF$ et $CEG$ sont isométriques. Cela aurait cependant été beaucoup plus laborieux, et remarquer qu'il existe une rotation envoyant certains points sur d'autres points a ici permis de conclure très rapidement.
Cette technique peut bien sûr être utilisée avec les autres transformations du plan.
Pour illustrer la manière dont une telle transformation peut se révéler utile, considérons le problème suivant.
Problème
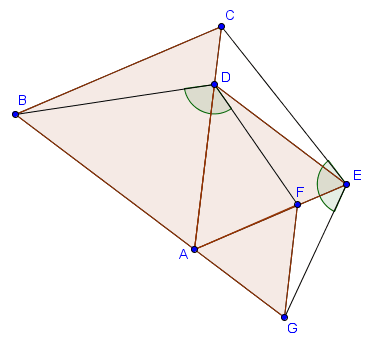
On a trois triangles équilatéraux $ABC$, $ADE$ et $AFG$ comme ci-dessous, tels que $D \in [AC]$ et $F \in [AE]$. Prouver que $\widehat{BDF} = \widehat{CEG}$.

Solution
Cette figure contient beaucoup d'angles de $60^\circ$, et pour cette raison il est naturel de songer à utiliser une rotation de $60^\circ$ autour de $A$. Regardons les images de certains points de la figure sous une rotation de $60^\circ$ (de sens trigonométrique) autour de $A$. On voit que l'image de $C$ est exactement $B$, l'image de $E$ est exactement $D$ et l'image de $G$ est exactement $F$. Du coup, comme une rotation est une isométrie, elle préserve les angles et on obtient directement que $\widehat{BDF} = \widehat{CEG}$ ! En fait, on a même que les triangles $BDF$ et $CEG$ sont isométriques.
Il aurait bien sûr été possible de montrer, sans utiliser de rotation, que les deux triangles $BDF$ et $CEG$ sont isométriques. Cela aurait cependant été beaucoup plus laborieux, et remarquer qu'il existe une rotation envoyant certains points sur d'autres points a ici permis de conclure très rapidement.
Cette technique peut bien sûr être utilisée avec les autres transformations du plan.