Transformations du plan
Prérequis
Résumé
Les transformations du plan classiques, à savoir les symétries, rotations, translations et homothéties, peuvent être très utiles dans la résolution d'un problème. Les homothéties permettent notamment de montrer des résultats a priori bien compliqués, comme l'existence de la droite d'Euler et du cercle d'Euler dans un triangle.
Ce chapitre a été écrit par N. Radu et mis en ligne le 20 avril 2016.
1. Isométries
Une transformation du plan est, comme son nom l'indique, une transformation particulière que l'on peut appliquer aux objets dans le plan. Il existe plusieurs types de transformations du plan, et nous nous penchons d'abord sur les plus connues : les rotations, translations et symétries orthogonales. Dans cette section, tous les angles seront orientés.
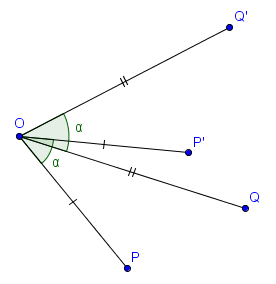
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par rotation de centre $O$ et d'angle $\alpha = 45^\circ$. Pour trouver $P'$ et $Q'$, on voit qu'il suffit de faire tourner $P$ et $Q$ autour de $O$ avec un angle de $45^\circ$.
Les rotations ont une propriété fondamentale : ce sont des isométries.
Il existe un type de rotation particulier : les symétries centrales. Étant donné un point $O$, la symétrie centrale de centre $O$ est un autre nom pour la rotation de centre $O$ et d'angle $\pi$ (c'est-à-dire $180^\circ$). La symétrie centrale est plus facile à définir : l'image du point $P$ par la symétrie centrale de centre $O$ est juste le point $P'$ tel que $O$ soit le milieu de $[PP']$. Le point $P'$ est alors le symétrique de $P$ par rapport à $O$.
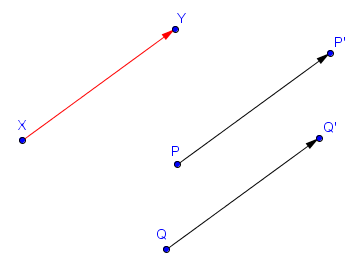
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la translation appliquant $X$ sur $Y$.
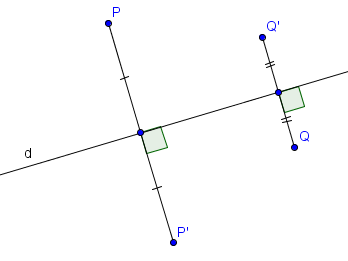
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la symétrie orthogonale d'axe $d$.
Certaines isométries ont des propriétés supplémentaires, qui découlent généralement de leur définition. On a par exemple que l'image d'une droite par une translation ou par une symétrie centrale est une droite qui lui est parallèle.
Rotations
Étant donné un point $O$ du plan et un angle $\alpha \in [0, 2\pi[$ (en radians), on peut considérer la rotation de centre $O$ et d'angle $\alpha$. Intuitivement, il s'agit de faire tourner le plan autour de $O$, d'un angle $\alpha$. Plus précisément et par définition, l'image d'un point $P$ par la rotation de centre $O$ et d'angle $\alpha$ est l'unique point $P'$ tel que $|OP'| = |OP|$ et $\widehat{POP'} = \alpha$ (en angles orientés, de sorte qu'il n'y ait qu'un seul tel point et non deux).Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par rotation de centre $O$ et d'angle $\alpha = 45^\circ$. Pour trouver $P'$ et $Q'$, on voit qu'il suffit de faire tourner $P$ et $Q$ autour de $O$ avec un angle de $45^\circ$.

Les rotations ont une propriété fondamentale : ce sont des isométries.
Propriété
Une rotation est une isométrie, c'est-à-dire une transformation qui préserve les longueurs. Autrement dit, si $P'$ et $Q'$ sont les images de deux points $P$ et $Q$ par une même rotation, alors $|P'Q'| = |PQ|$.
Il existe un type de rotation particulier : les symétries centrales. Étant donné un point $O$, la symétrie centrale de centre $O$ est un autre nom pour la rotation de centre $O$ et d'angle $\pi$ (c'est-à-dire $180^\circ$). La symétrie centrale est plus facile à définir : l'image du point $P$ par la symétrie centrale de centre $O$ est juste le point $P'$ tel que $O$ soit le milieu de $[PP']$. Le point $P'$ est alors le symétrique de $P$ par rapport à $O$.
Translations
Étant donnés deux points $X$ et $Y$ du plan, on peut considérer la translation appliquant $X$ sur $Y$. Intuitivement, il s'agit de faire glisser le plan de sorte à ce que $X$ devienne $Y$. Plus précisément, l'image d'un point $P$ par la translation appliquant $X$ sur $Y$ est l'unique point $P'$ tel que $\vec{PP'} = \vec{XY}$. Pour ceux ne connaissant pas la notion de vecteurs, cela signifie simplement que la flèche reliant $P$ à $P'$ doit être exactement la même (c'est-à-dire de même longueur, direction et sens) que celle reliant $X$ à $Y$.Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la translation appliquant $X$ sur $Y$.

Propriété
Une translation est une isométrie.
Symétries orthogonales
Étant donnée une droite $d$ du plan, on peut considérer la symétrie orthogonale d'axe $d$. Intuitivement, on peut penser à $d$ comme à un miroir. Par définition, l'image d'un point $P$ par la symétrie orthogonale d'axe $d$ est l'unique point $P'$ tel que $PP'$ est perpendiculaire à $d$ et le milieu de $[PP']$ se trouve sur $d$. On dit que $P'$ est le symétrique de $P$ par rapport à l'axe $d$.Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par la symétrie orthogonale d'axe $d$.

Propriété
Une symétrie orthogonale est une isométrie. De plus, si $P'$ est l'image de $P$ par une symétrie orthogonale, alors $P$ est l'image de $P'$ par cette même symétrie.
Propriétés
Les rotations, translations et symétries orthogonales partagent un grand nombre de propriétés, du fait que ce sont des isométries.Propriétés des isométries
Les isométries conservent :
- la longueur des segments (par définition d'isométrie) : $|P'Q'| = |PQ|$;
- l'amplitude des angles : $\widehat{P'Q'R'} = \widehat{PQR}$;
- l'alignement des points : si $P$, $Q$ et $R$ sont alignés, alors $P'$, $Q'$ et $R'$ sont alignés (c'est un cas particulier du point 2);
- le parallélisme des droites : si $PQ$ et $RS$ sont parallèles, alors $P'Q'$ et $R'S'$ sont parallèles;
- la perpendicularité des droites : si $PQ$ et $RS$ sont perpendiculaires, alors $P'Q'$ et $R'S'$ sont perpendiculaires (cas particulier du point 2);
- le milieu d'un segment : si $M$ est le milieu de $[PQ]$, alors $M'$ est le milieu de $[P'Q']$ (conséquence des points 1 et 3);
- le périmètre et l'aire des figures.
- ...
Certaines isométries ont des propriétés supplémentaires, qui découlent généralement de leur définition. On a par exemple que l'image d'une droite par une translation ou par une symétrie centrale est une droite qui lui est parallèle.
Classification des isométries
Comme vu plus haut, les rotations, translations et symétries orthogonales sont des isométries. En fait, il s'agit des seules isométries du plan (à une petite exception près) !Classification des isométries du plan
Soit $f$ une isométrie du plan, c'est-à-dire une fonction $f : \mathbb{R}^2 \to \mathbb{R}^2$ qui est une bijection et qui préserve les longueurs.
- Si $f$ a trois points fixes non-alignés, alors $f$ est l'identité.
- Si $f$ n'est pas l'identité et a au moins deux points fixes $A$ et $B$, alors $f$ est la symétrie orthogonale d'axe $AB$.
- Si $f$ a un unique point fixe $A$, alors $f$ est une rotation de centre $A$.
- Si $f$ n'a pas de point fixe, alors:
- soit $f$ est une translation,
- soit $f$ est la composée d'une symétrie orthogonale et d'une translation de vecteur parallèle à l'axe de symétrie.
2. Homothéties
Les homothéties sont d'autres transformations du plan classiques, mais qui ne sont (généralement) pas des isométries.
Définissons d'abord l'homothétie de façon rigoureuse. L'image d'un point $P$ par l'homothétie de centre $O$ et de rapport $k$ est l'unique point $P'$ tel que $\vec{OP'} = k \cdot \vec{OP}$. Pour ceux ne connaissant pas les vecteurs, cela revient à dire la chose suivante :
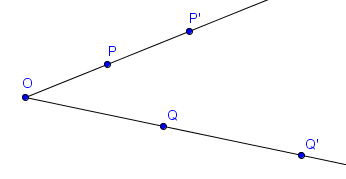
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $2$.
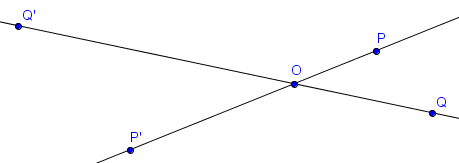
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $-2$.
On remarque qu'appliquer une homothétie de centre $O$ et de rapport $k$ avec $k < 0$ revient exactement à effectuer une homothétie de rapport $|k|$ puis une symétrie centrale.
Définition
Étant donné un point $O$ du plan et un réel non-nul $k$, on définit l'homothétie de centre $O$ et de rapport $k$. Intuitivement, lorsque $k > 1$ cela consiste à zoomer la figure sur le point $O$ (et plus $k$ est grand, plus on zoome). Si $0 < k < 1$ alors il s'agit plutôt d'un dézoom de la figure, toujours centré en le point $O$. Le cas où $k < 0$ est un peu plus particulier : nous en discuterons plus bas.Définissons d'abord l'homothétie de façon rigoureuse. L'image d'un point $P$ par l'homothétie de centre $O$ et de rapport $k$ est l'unique point $P'$ tel que $\vec{OP'} = k \cdot \vec{OP}$. Pour ceux ne connaissant pas les vecteurs, cela revient à dire la chose suivante :
- Si $k > 0$, alors $P'$ est le point de la droite $OP$ du même côté de $O$ que $P$ et tel que $|OP'| = k \cdot |OP|$.
- Si $k < 0$, alors $P'$ est le point de la droite $OP$ du côté opposé de $O$ que $P$ et tel que $|OP'| = |k| \cdot |OP|$.
Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $2$.

Sur la figure suivante, $P'$ et $Q'$ sont les images respectives de $P$ et $Q$ par l'homothétie de centre $O$ et de rapport $-2$.

On remarque qu'appliquer une homothétie de centre $O$ et de rapport $k$ avec $k < 0$ revient exactement à effectuer une homothétie de rapport $|k|$ puis une symétrie centrale.
Propriétés
Mis à part lorsque $k = \pm 1$, on voit qu'une homothétie de rapport $k$ n'est pas une isométrie. Les homothéties ont toutefois des propriétés similaires aux isométries.Propriété des homothéties
Une homothétie de rapport $k$ :
- multiplie les longueurs par $|k|$ : $|P'Q'| = |k| \cdot |PQ|$;
- conserve l'amplitude des angles;
- conserve l'alignement des points;
- conserve le parallélisme des droites;
- conserve la perpendicularité des droites;
- conserve le milieu d'un segment;
- multiplie les périmètres des figures par $|k|$ et les aires des figures par $k^2$;
- envoie toute droite sur une droite parallèle.
- ...
3. Utilisation
Lorsque l'on est en présence d'un problème de géométrie, appliquer à tout le plan une transformation du type rotation, translation, symétrie orthogonale ou homothétie n'a pas réellement d'intérêt. En effet, une telle transformation revient juste à faire tourner la figure, la bouger ou zoomer dessus, mais cela ne va bien sûr aucunement aider à résoudre le problème.
Pour illustrer la manière dont une telle transformation peut se révéler utile, considérons le problème suivant.
Il aurait bien sûr été possible de montrer, sans utiliser de rotation, que les deux triangles $BDF$ et $CEG$ sont isométriques. Cela aurait cependant été beaucoup plus laborieux, et remarquer qu'il existe une rotation envoyant certains points sur d'autres points a ici permis de conclure très rapidement.
Cette technique peut bien sûr être utilisée avec les autres transformations du plan.
Pour illustrer la manière dont une telle transformation peut se révéler utile, considérons le problème suivant.
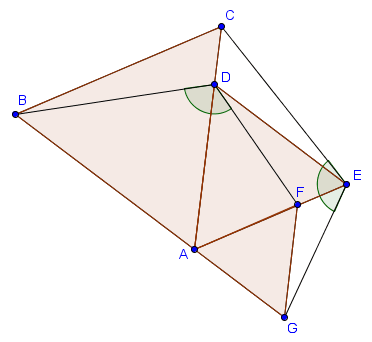
Problème
On a trois triangles équilatéraux $ABC$, $ADE$ et $AFG$ comme ci-dessous, tels que $D \in [AC]$ et $F \in [AE]$. Prouver que $\widehat{BDF} = \widehat{CEG}$.

Solution
Cette figure contient beaucoup d'angles de $60^\circ$, et pour cette raison il est naturel de songer à utiliser une rotation de $60^\circ$ autour de $A$. Regardons les images de certains points de la figure sous une rotation de $60^\circ$ (de sens trigonométrique) autour de $A$. On voit que l'image de $C$ est exactement $B$, l'image de $E$ est exactement $D$ et l'image de $G$ est exactement $F$. Du coup, comme une rotation est une isométrie, elle préserve les angles et on obtient directement que $\widehat{BDF} = \widehat{CEG}$ ! En fait, on a même que les triangles $BDF$ et $CEG$ sont isométriques.
Il aurait bien sûr été possible de montrer, sans utiliser de rotation, que les deux triangles $BDF$ et $CEG$ sont isométriques. Cela aurait cependant été beaucoup plus laborieux, et remarquer qu'il existe une rotation envoyant certains points sur d'autres points a ici permis de conclure très rapidement.
Cette technique peut bien sûr être utilisée avec les autres transformations du plan.
4. Droite d'Euler
Dans un triangle $ABC$, les quatre points particuliers les plus fréquemment étudiés sont le centre du cercle circonscrit $O$, le centre du cercle inscrit $I$, l'orthocentre $H$ et le centre de gravité $G$. Il s'avère en fait que les points $O$, $H$ et $G$ sont toujours alignés, et la droite qu'ils forment s'appelle la droite d'Euler. (Si le triangle est équilatéral, les trois points sont confondus et il n'y a donc pas de droite d'Euler). Plus précisément, on a le résultat suivant. La démonstration de ce résultat est aussi intéressante que le résultat lui-même, car elle fait intervenir une homothétie et donne donc un autre exemple d'utilisation des transformations du plan.
Théorème (droite d'Euler)
Soit $ABC$ un triangle, $O$ son centre du cercle circonscrit, $H$ son orthocentre et $G$ son centre de gravité. Alors $H$, $G$ et $O$ sont alignés dans cet ordre (c'est-à-dire que $G \in [OH]$) et $|HG| = 2 \cdot |GO|$.
Démonstration
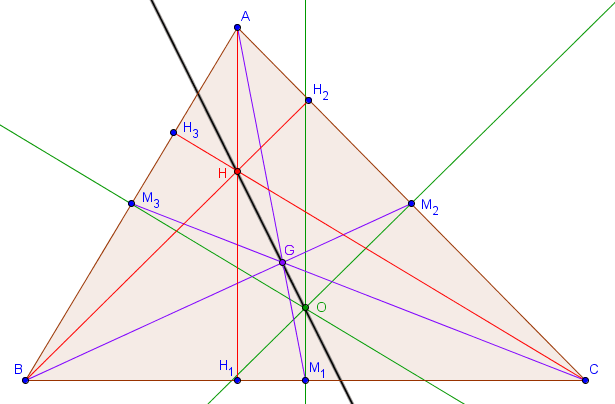
Sur le dessin ci-dessous, les points $M_1, M_2, M_3$ sont les milieux des trois côtés et les points $H_1, H_2, H_3$ sont les pieds des trois hauteurs.
Considérons l'homothétie $h$ de centre $G$ et de rapport $-\frac{1}{2}$. Puisque $G$ se trouve au tiers de chaque médiane, l'image de $A$ par $h$ est $M_1$, l'image de $B$ est $M_2$ et l'image de $C$ est $M_3$.
L'homothétie $h$ envoie donc la hauteur $AH_1$ sur une droite passant par $M_1$ et qui lui est parallèle. Comme $AH_1$ est perpendiculaire à $BC$, cette image doit donc également être perpendiculaire à $BC$ et il ne peut donc s'agir que de la médiatrice de $[BC]$. De la même manière, l'image par $h$ de $BH_2$ est la médiatrice de $[AC]$ et l'image de $CH_3$ est la médiatrice de $[AB]$. L'intersection $H$ des trois hauteurs est donc envoyée par $h$ sur l'intersection des trois médiatrices, à savoir $O$.
On en déduit directement que $H$, $G$ et $O$ sont alignés et que $|GO| = \frac{1}{2} \cdot |GH|$.
Considérons l'homothétie $h$ de centre $G$ et de rapport $-\frac{1}{2}$. Puisque $G$ se trouve au tiers de chaque médiane, l'image de $A$ par $h$ est $M_1$, l'image de $B$ est $M_2$ et l'image de $C$ est $M_3$.
L'homothétie $h$ envoie donc la hauteur $AH_1$ sur une droite passant par $M_1$ et qui lui est parallèle. Comme $AH_1$ est perpendiculaire à $BC$, cette image doit donc également être perpendiculaire à $BC$ et il ne peut donc s'agir que de la médiatrice de $[BC]$. De la même manière, l'image par $h$ de $BH_2$ est la médiatrice de $[AC]$ et l'image de $CH_3$ est la médiatrice de $[AB]$. L'intersection $H$ des trois hauteurs est donc envoyée par $h$ sur l'intersection des trois médiatrices, à savoir $O$.
On en déduit directement que $H$, $G$ et $O$ sont alignés et que $|GO| = \frac{1}{2} \cdot |GH|$.

5. Cercle d'Euler
Le cercle d'Euler d'un triangle, aussi appelé cercle des neufs points est le cercle dont l'existence est assurée par la proposition suivante. Nous conseillons vivement au lecteur d'essayer de comprendre sa démonstration, qui fait à nouveau intervenir des homothéties.
À noter que l'on peut retenir les points 2 et 3 en retenant simplement que le cercle d'Euler est l'image du cercle circonscrit par l'homothétie de centre $H$ et de rapport $\frac{1}{2}$. Comme les milieux des côtés et les pieds des hauteurs sont sur le cercle d'Euler, ces résultats en découlent.
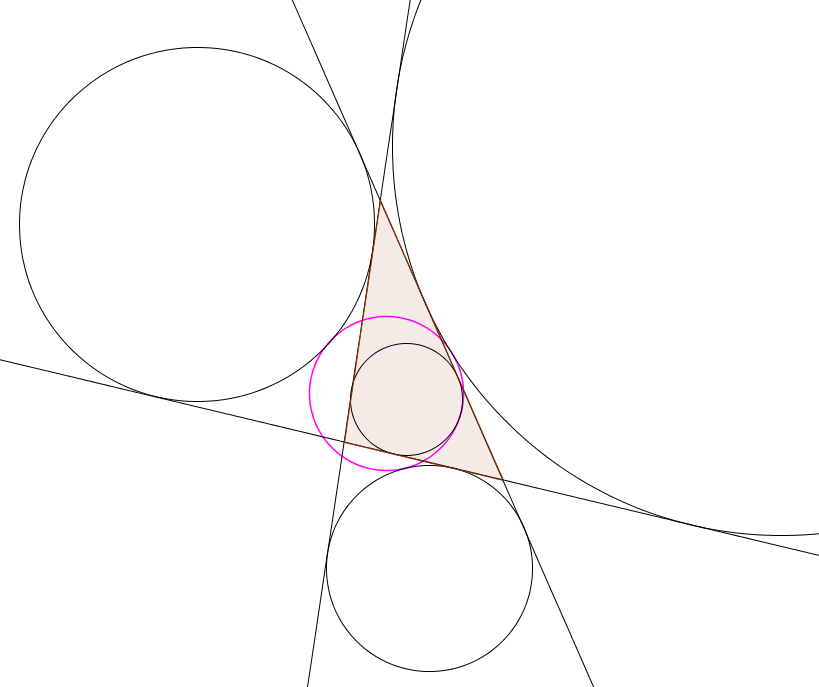
Existence du cercle d'Euler
Théorème (cercle d'Euler)
Soit $ABC$ un triangle, $M_1, M_2, M_3$ les milieux des côtés $[BC]$, $[CA]$ et $[AB]$, $H$ l'orthocentre de $ABC$, et $H_1, H_2, H_3$ les pieds des hauteurs relatives à $A$, $B$ et $C$. Il existe un unique cercle passant par $M_1, M_2, M_3, H_1, H_2, H_3$ ainsi que les milieux de $[HA]$, $[HB]$ et $[HC]$. Ce cercle est appelé le cercle d'Euler de $ABC$, et son centre se situe sur la droite d'Euler de $ABC$.
Démonstration
Considérons tout d'abord l'homothétie $h_G$ de centre $G$ et de rapport $-\frac{1}{2}$. Nous avons déjà vu dans le point théorique précédent que $h_G$ envoie $A$, $B$ et $C$ sur $M_1$, $M_2$ et $M_3$ respectivement, ainsi que $H$ sur $O$, le centre du cercle circonscrit à $ABC$. En particulier, le cercle circonscrit $\Gamma$ à $ABC$ a pour image le cercle circonscrit à $M_1M_2M_3$. Notons ce dernier cercle $\mathcal{C}$. Celui-ci passe par $M_1$, $M_2$ et $M_3$ et on sait déjà que son centre $E$ est l'image de $O$ par l'homothétie $h_G$. Cela signifie que $E$ se situe sur la droite d'Euler, et on sait même que $|EG| = \frac{1}{2} \cdot |GO|$ (avec $G \in [OE]$). $(1)$
Nous devons à présent montrer que le cercle $\mathcal{C}$ contient également les six autres points mentionnés dans l'énoncé. Avant cela, remarquons la chose suivante. Notons $B'$ le symétrique de $B$ par rapport à $O$. Comme $O$ est le centre de $\Gamma$, il est clair que $B' \in \Gamma$. De plus, l'image du segment $[BH]$ par $h_G$ est le segment $[M_2O]$. Cela signifie que, dans le triangle $B'BH$, le segment $[M_2O]$ est le segment reliant les milieux de deux côtés. Il en découle que $M_2$ est le milieu de $[B'H]$. Nous venons donc de montrer que le symétrique de $H$ par rapport à $M_2$, qui n'est autre que $B'$, appartient à $\Gamma$. De manière similaire, on trouve en fait que les symétriques de $H$ par rapport aux trois milieux $M_1, M_2, M_3$ sont tous sur $\Gamma$. $(2)$
Considérons à présent l'homothétie $h_H$ de centre $H$ et de rapport $\frac{1}{2}$. Nous venons en fait juste de prouver que l'image de $B'$ par $h_H$ est $M_2$. De la même manière, $M_1$ et $M_3$ sont les images par $h_H$ de deux points du cercle $\Gamma$. Il en découle que $\mathcal{C}$ est l'image de $\Gamma$ par $h_H$. (À noter qu'on a déjà vu que $\mathcal{C}$ était l'image de $\Gamma$ par $h_G$ qui est une toute autre homothétie ! Tout cela est plutôt magique.) Comme les images de $A$, $B$ et $C$ (qui se situent sur $\Gamma$) par $h_H$ sont les milieux respectifs de $[AH]$, $[BH]$ et $[CH]$, on en déduit que ces milieux se trouvent sur $\mathcal{C}$.
Enfin, notons $I_2$ la deuxième intersection de $BH$ avec $\Gamma$. Comme $[BB']$ est un diamètre de $\Gamma$, le triangle $BI_2B'$ est rectangle en $I_2$. Il s'ensuit que $B'I_2$ est parallèle à $AC$. Comme $M_2$ est le milieu de $[B'H]$, cela signifie que $[M_2H_2]$ est le segment joignant les milieux de deux côtés du triangle $HB'I_2$ et donc en particulier que $H_2$ est le milieu de $[HI_2]$. Les symétriques de l'orthocentre par rapport aux côtés se trouvent donc tous sur $\Gamma$, ce qui est à nouveau un résultat remarquable $(3)$. L'image de $I_2$ par $h_H$ est donc exactement $H_2$, et cela implique que $H_2 \in \mathcal{C}$. De la même manière, on trouve que $H_1$ et $H_3$ se situent sur $\mathcal{C}$.
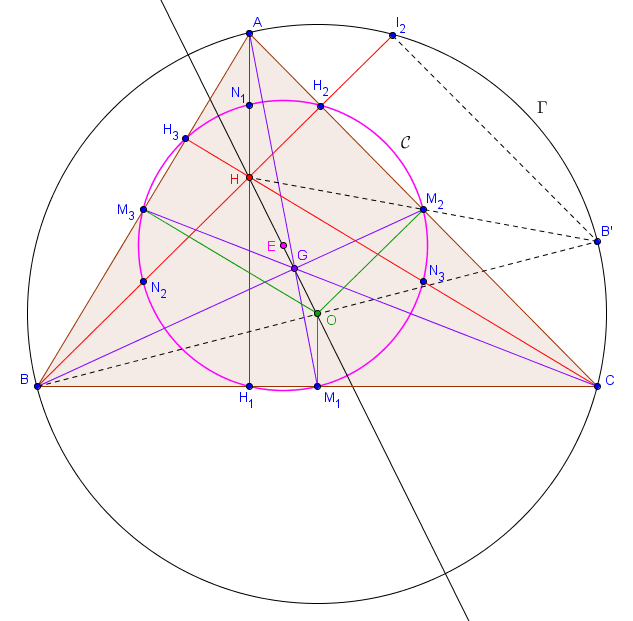
Nous devons à présent montrer que le cercle $\mathcal{C}$ contient également les six autres points mentionnés dans l'énoncé. Avant cela, remarquons la chose suivante. Notons $B'$ le symétrique de $B$ par rapport à $O$. Comme $O$ est le centre de $\Gamma$, il est clair que $B' \in \Gamma$. De plus, l'image du segment $[BH]$ par $h_G$ est le segment $[M_2O]$. Cela signifie que, dans le triangle $B'BH$, le segment $[M_2O]$ est le segment reliant les milieux de deux côtés. Il en découle que $M_2$ est le milieu de $[B'H]$. Nous venons donc de montrer que le symétrique de $H$ par rapport à $M_2$, qui n'est autre que $B'$, appartient à $\Gamma$. De manière similaire, on trouve en fait que les symétriques de $H$ par rapport aux trois milieux $M_1, M_2, M_3$ sont tous sur $\Gamma$. $(2)$
Considérons à présent l'homothétie $h_H$ de centre $H$ et de rapport $\frac{1}{2}$. Nous venons en fait juste de prouver que l'image de $B'$ par $h_H$ est $M_2$. De la même manière, $M_1$ et $M_3$ sont les images par $h_H$ de deux points du cercle $\Gamma$. Il en découle que $\mathcal{C}$ est l'image de $\Gamma$ par $h_H$. (À noter qu'on a déjà vu que $\mathcal{C}$ était l'image de $\Gamma$ par $h_G$ qui est une toute autre homothétie ! Tout cela est plutôt magique.) Comme les images de $A$, $B$ et $C$ (qui se situent sur $\Gamma$) par $h_H$ sont les milieux respectifs de $[AH]$, $[BH]$ et $[CH]$, on en déduit que ces milieux se trouvent sur $\mathcal{C}$.
Enfin, notons $I_2$ la deuxième intersection de $BH$ avec $\Gamma$. Comme $[BB']$ est un diamètre de $\Gamma$, le triangle $BI_2B'$ est rectangle en $I_2$. Il s'ensuit que $B'I_2$ est parallèle à $AC$. Comme $M_2$ est le milieu de $[B'H]$, cela signifie que $[M_2H_2]$ est le segment joignant les milieux de deux côtés du triangle $HB'I_2$ et donc en particulier que $H_2$ est le milieu de $[HI_2]$. Les symétriques de l'orthocentre par rapport aux côtés se trouvent donc tous sur $\Gamma$, ce qui est à nouveau un résultat remarquable $(3)$. L'image de $I_2$ par $h_H$ est donc exactement $H_2$, et cela implique que $H_2 \in \mathcal{C}$. De la même manière, on trouve que $H_1$ et $H_3$ se situent sur $\mathcal{C}$.

Propriétés annexes
Au cours de la preuve précédente, certains résultats annexes sont apparus (dont les énoncés ne font pas toujours intervenir le cercle d'Euler, ce qui les rend donc peut-être d'autant plus intéressants). Nous les mettons à nouveau en évidence ici (voir $(1)$, $(2)$ et $(3)$ dans la preuve pour les démonstrations).Autres propriétés
- La droite d'Euler contient le centre du cercle d'Euler, et on a $|OG| = 2 \cdot |GE|$ (avec $G \in [EO]$).
- Les trois symétriques de l'orthocentre par rapport aux milieux des côtés se trouvent sur le cercle circonscrit.
- Les trois symétriques de l'orthocentre par rapport aux côtés se trouvent sur le cercle circonscrit.
À noter que l'on peut retenir les points 2 et 3 en retenant simplement que le cercle d'Euler est l'image du cercle circonscrit par l'homothétie de centre $H$ et de rapport $\frac{1}{2}$. Comme les milieux des côtés et les pieds des hauteurs sont sur le cercle d'Euler, ces résultats en découlent.
Théorème de Feuerbach
Le cercle d'Euler a également la propriété d'être tangent intérieurement au cercle inscrit et tangent extérieurement aux trois cercles exinscrits au triangle. Ce résultat est appelé théorème de Feuerbach, et les quatre points de tangence sont appelés les points de Feuerbach.