Rapports anharmoniques
Définitions
Rapport anharmonique de $4$ points alignés
Étant donnés $4$ points distincts $A, B, C, D$ sur une même droite, on définit le rapport anharmonique $(A,B;C,D)$ comme suit. Rappelons que lorsque $X, Y, Z, T$ sont quatre points avec $XY$ parallèle à $ZT$, le rapport orienté $\frac{\overline{XY}}{\overline{ZT}}$ est défini comme étant égal à $\frac{|XY|}{|ZT|}$ ou $-\frac{|XY|}{|ZT|}$ selon que $[XY)$ et $[ZT)$ pointent dans le même sens ou non. La notion de rapport de section est également définie à partir de rapports orientés, voir le chapitre à ce sujet.Définition (rapport anharmonique de $4$ points)
Le rapport anharmonique de quatre points $A,B,C,D$ distincts alignés, aussi appelé birapport, est défini par
$$(A,B;C,D) = \frac{r_{DC}(A)}{r_{DC}(B)} = \frac{\frac{\overline{AC}}{\overline{AD}}}{\frac{\overline{BC}}{\overline{BD}}}.$$ Il dépend de l'ordre dans lequel les points $A, B, C, D$ sont considérés.
$$(A,B;C,D) = \frac{r_{DC}(A)}{r_{DC}(B)} = \frac{\frac{\overline{AC}}{\overline{AD}}}{\frac{\overline{BC}}{\overline{BD}}}.$$ Il dépend de l'ordre dans lequel les points $A, B, C, D$ sont considérés.
Comme toutes premières propriétés du rapport anharmonique, on peut voir que les formules suivantes sont vérifiées :
- $(B,A;C,D) = \dfrac{1}{(A,B;C,D)}$
- $(C,D;A,B) = (A,B;C,D)$
Lorsqu'on parle du rapport anharmonique $(A,B;C,D)$, on imagine souvent que $C$ et $D$ sont fixés et qu'on regarde la position de $A$ et $B$ par rapport à ces deux points $C$ et $D$ fixés. La deuxième égalité ci-dessus montre que regarder $A$ et $B$ par rapport à $C$ et $D$ revient en fait au même que regarder $C$ et $D$ par rapport à $A$ et $B$.
Division harmonique
Lorsque le rapport anharmonique de quatre points vaut $-1$, on parle de division harmonique :Définition (division harmonique)
On dit que quatres points alignés $A, B, C, D$ forment une division harmonique si $(A,B;C,D) = -1$. On dit aussi que $B$ est le conjugué harmonique de $A$ par rapport à $C,D$.
Dans le cas d'une division harmonique, il faut seulement préciser quelle paire de points (ici $A,B$) est comparée à quelle autre paire (ici $C,D$). En effet, $A, B, C, D$ forment une division harmonique si et seulement si l'une des quantités $(A,B;C,D)$, $(B,A;C,D)$, $(A,B;D,C)$, $(B,A;D,C)$, $(C,D;A,B)$, $(D,C;A,B)$, $(C,D;B,A)$, $(D,C;B,A)$ est égale à $-1$.
Si $C$ et $D$ sont fixés, alors tout point de la droite $CD$ (différent de $C$ et $D$) possède un unique conjugué harmonique par rapport à $C, D$, à l'exception du milieu $M$ de $[CD]$ qui n'en possède pas. De plus, le conjugué d'un point sur le segment $[CD]$ se trouve à l'extérieur de $[CD]$, et vice versa. Cela découle des propriétés du rapport de section : on a vu que la fonction $X \mapsto r_{DC}(X)$ définit une bijection entre les points de $DC$ différents de $D$ et les réels différents de $1$. Comme $r_{DC}(M) = -1$, $M$ ne possède pas de conjugué harmonique par rapport à $C,D$ : il n'existe aucun $X$ tel que $r_{DC}(X) = 1$.
Rapport anharmonique de $4$ droites concourantes
Il est aussi possible de définir le rapport anharmonique de $4$ droites concourantes. La définition se base sur la propriété suivante :Proposition (définition du rapport anharmonique de $4$ droites)
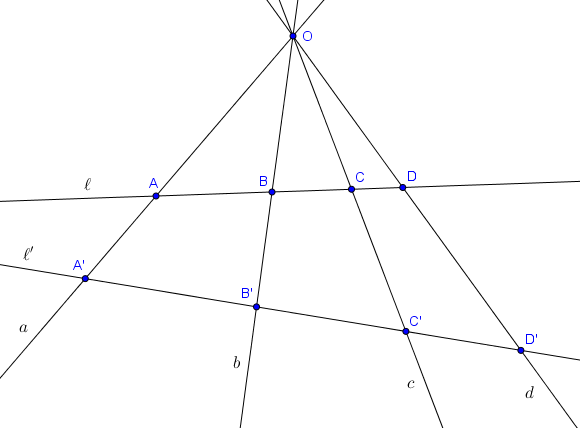
Soit $O$ un point et $a, b, c, d$ quatre droites distinctes passant par $O$. Soit $\ell$ une droite ne passant pas par $O$ et qui n'est pas parallèle à $a, b, c$ ou $d$. On note $A, B, C, D$ les intersections de $\ell$ avec $a, b, c$ et $d$. Alors le rapport anharmonique $(A,B;C,D)$ ne dépend pas de la droite $\ell$ choisie. Cette quantité est appelée le rapport anharmonique $(a,b;c,d)$ des droites $a, b, c, d$.
Démonstration
En utilisant la loi des sinus dans les triangles $OAC$, $OAD$, $OBC$ et $OBD$, on trouve la formule suivante, où les angles sont orientés :
$$(A,B;C,D) = \frac{\frac{\sin \widehat{AOC}}{\sin \widehat{AOD}}}{\frac{\sin\widehat{BOC}}{\sin\widehat{BOD}}}$$ Intuitivement la preuve est terminée, puisque cette quantité ne dépend pas de la droite $\ell$ choisie (mais uniquement des angles que les droites $a, b, c, d$ forment entre elles). Il y cependant une subtilité à laquelle il faut faire attention : chaque point $A$, $B$, $C$, $D$ peut se situer d'un côté de $O$ ou de l'autre (sur sa droite $a$, $b$, $c$, $d$). Les sinus des angles dans la formule ci-dessous, en valeur absolue, ne dépendent pas de la droite $\ell$, mais leurs signes peuvent changer ! Une analyse plus détaillée des cas montre toutefois que le signe de $(A,B;C,D)$ reste toujours le même, indépendamment de $\ell$.
$$(A,B;C,D) = \frac{\frac{\sin \widehat{AOC}}{\sin \widehat{AOD}}}{\frac{\sin\widehat{BOC}}{\sin\widehat{BOD}}}$$ Intuitivement la preuve est terminée, puisque cette quantité ne dépend pas de la droite $\ell$ choisie (mais uniquement des angles que les droites $a, b, c, d$ forment entre elles). Il y cependant une subtilité à laquelle il faut faire attention : chaque point $A$, $B$, $C$, $D$ peut se situer d'un côté de $O$ ou de l'autre (sur sa droite $a$, $b$, $c$, $d$). Les sinus des angles dans la formule ci-dessous, en valeur absolue, ne dépendent pas de la droite $\ell$, mais leurs signes peuvent changer ! Une analyse plus détaillée des cas montre toutefois que le signe de $(A,B;C,D)$ reste toujours le même, indépendamment de $\ell$.

Faisceau harmonique
La définition suivante est l'équivalent de la division harmonique pour les droites concourantes :Définition (faisceau harmonique)
Quatre droites concourantes $a, b, c, d$ forment un faisceau harmonique si $(a,b;c,d) = -1$. On dira également que $a$ et $b$ sont conjugués harmoniques par rapport à $c,d$.