Introduction aux inégalités
Second degré
On peut étudier en toute généralité le signe d'un polynôme du second degré. Cette matière va sembler évidente à ceux qui l'ont déjà vue en secondaire, ce qui est normal.
Un polynôme du second degré est une expression de la forme $ax^2 + bx + c$ où $a,b$ et $c$ sont des constantes réelles. On demande aussi généralement que $a \neq 0$ puisque si $a = 0$, alors on a simplement l'expression $bx + c$ qui est bien plus simple à étudier.
Au vu de la formule pour $x_1$ et $x_2$, on comprend mieux pourquoi il n'y a pas de racines réelles quand $b^2 - 4ac < 0$ et pourquoi il n'y a qu'une seule racine lorsque $b^2 - 4ac = 0$.
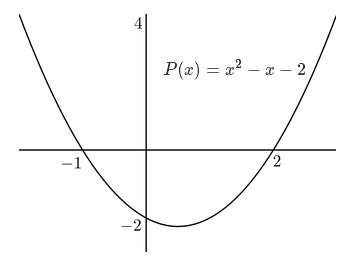
Prenons par exemple le polynôme $P(x) = x^2 - x - 2$. On a $b^2 - 4ac = (-1)^2 - 4(-2) = 9 > 0$ et on est donc dans ce cas dans la dernière configuration du résultat. On calcule aisément $x_1 = -1$ et $x_2 = 2$. Le polynôme est donc du même signe que $a$, c'est à dire positif, pour $x \leq x_1 = -1$ et pour $x \geq x_2 = 2$. Le graphe de cette fonction est le suivant :
$$x^2+y^2+4x+4 \geq y(2x+4).$$ On peut ici penser à $x$ comme étant un simple paramètre, et l'inégalité n'est alors rien d'autre qu'une inégalité impliquant un polynôme du second degré en $y$ :
$$y^2 - (2x+4)y + x^2+4x+4 \geq 0$$ On calcule alors le discriminant $b^2-4ac$ : il vaut ici $(2x+4)^2 - 4(x^2+4x+4) = 0$, ce qui signifie que ce polynôme en $y$ est toujours du signe de $a$, c'est-à-dire positif comme voulu. Notre exemple n'était ici pas très compliqué (on peut en fait remarquer qu'il s'agit simplement de l'inégalité $(x-y+2)^2 \geq 0$), mais cette méthode peut fonctionner dans des cas plus complexes. Il faudra alors discuter les différents cas selon le signe du discriminant.
Un polynôme du second degré est une expression de la forme $ax^2 + bx + c$ où $a,b$ et $c$ sont des constantes réelles. On demande aussi généralement que $a \neq 0$ puisque si $a = 0$, alors on a simplement l'expression $bx + c$ qui est bien plus simple à étudier.
Proposition
Soient $a, b, c \in \mathbb{R}$ avec $a \neq 0$ et $P(x) = ax^2 + bx + c$.
- Si $b^2 - 4ac < 0$, alors $P(x)$ est du signe de $a$ pour tout $x \in \mathbb{R}$ et ne s'annule jamais;
- Si $b^2 - 4ac = 0$, alors $P(x)$ est du signe de $a$ pour tout $x \in \mathbb{R}$ et s'annule en $\frac{-b}{2a}$;
- Si $b^2 - 4ac > 0$, alors $P(x)$ s'annule en deux points $x_1 < x_2$ qui sont appelés ses racines et il est du signe de $a$ pour $x \in \ \left]-\infty, x_1\right[\ \cup \ \left]x_2, +\infty\right[$ et du signe opposé pour tout $x \in \ ]x_1, x_2[$.
Les racines $x_1$ et $x_2$ sont données (éventuellement dans l'ordre inverse lorsque $a < 0$) par
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
Au vu de la formule pour $x_1$ et $x_2$, on comprend mieux pourquoi il n'y a pas de racines réelles quand $b^2 - 4ac < 0$ et pourquoi il n'y a qu'une seule racine lorsque $b^2 - 4ac = 0$.
Prenons par exemple le polynôme $P(x) = x^2 - x - 2$. On a $b^2 - 4ac = (-1)^2 - 4(-2) = 9 > 0$ et on est donc dans ce cas dans la dernière configuration du résultat. On calcule aisément $x_1 = -1$ et $x_2 = 2$. Le polynôme est donc du même signe que $a$, c'est à dire positif, pour $x \leq x_1 = -1$ et pour $x \geq x_2 = 2$. Le graphe de cette fonction est le suivant :

Démonstration
L'idée est d'isoler $x$ dans un carré parfait et de ne garder que des constantes à l'extérieur :
$$\begin{align*}
P(x) = ax^2 + bx + c & =
a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a}\\
& =
a\left(\left(x + \frac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a^2}\right).
\end{align*}$$ Pour que $P(x)$ soit du signe de $a$, il faut donc que
$$\left(x + \frac{b}{2a}\right)^2 \geq \frac{b^2 - 4ac}{4a^2}.$$ Le membre de gauche est positif car c'est un carré parfait. Le membre de droite est du signe de $b^2 - 4ac$ car $4a^2 \geq 0$. Dès lors, si $b^2 - 4ac \leq 0$, l'inégalité est vraie pour tout $x$.
Sinon, les deux membres sont positifs. Comme la fonction $f: x \mapsto \sqrt{x}$ est strictement croissante pour $x \in \mathbb{R}^+$, notre inégalité est équivalente à
$$\left|x + \frac{b}{2a}\right| \geq
\frac{\sqrt{b^2 - 4ac}}{2|a|}$$ ce qui est vrai lorsque $x \leq x_1$ ou $x \geq x_2$ où $x_1$ (respectivement $x_2$) est le plus petit (resp. le plus grand) des deux nombres
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
$$\begin{align*}
P(x) = ax^2 + bx + c & =
a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a}\\
& =
a\left(\left(x + \frac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a^2}\right).
\end{align*}$$ Pour que $P(x)$ soit du signe de $a$, il faut donc que
$$\left(x + \frac{b}{2a}\right)^2 \geq \frac{b^2 - 4ac}{4a^2}.$$ Le membre de gauche est positif car c'est un carré parfait. Le membre de droite est du signe de $b^2 - 4ac$ car $4a^2 \geq 0$. Dès lors, si $b^2 - 4ac \leq 0$, l'inégalité est vraie pour tout $x$.
Sinon, les deux membres sont positifs. Comme la fonction $f: x \mapsto \sqrt{x}$ est strictement croissante pour $x \in \mathbb{R}^+$, notre inégalité est équivalente à
$$\left|x + \frac{b}{2a}\right| \geq
\frac{\sqrt{b^2 - 4ac}}{2|a|}$$ ce qui est vrai lorsque $x \leq x_1$ ou $x \geq x_2$ où $x_1$ (respectivement $x_2$) est le plus petit (resp. le plus grand) des deux nombres
$$\frac{-b - \sqrt{b^2 - 4ac}}{2a} \quad \text{et} \quad \frac{-b + \sqrt{b^2 - 4ac}}{2a}.$$
Utilisation pratique
Lorsqu'on désire montrer une inégalité avec plusieurs variables, une bonne idée peut-être de n'en considérer qu'une seule comme étant une variable et de voir les autres comme des paramètres. Imaginons par exemple que l'on désire montrer l'inégalité$$x^2+y^2+4x+4 \geq y(2x+4).$$ On peut ici penser à $x$ comme étant un simple paramètre, et l'inégalité n'est alors rien d'autre qu'une inégalité impliquant un polynôme du second degré en $y$ :
$$y^2 - (2x+4)y + x^2+4x+4 \geq 0$$ On calcule alors le discriminant $b^2-4ac$ : il vaut ici $(2x+4)^2 - 4(x^2+4x+4) = 0$, ce qui signifie que ce polynôme en $y$ est toujours du signe de $a$, c'est-à-dire positif comme voulu. Notre exemple n'était ici pas très compliqué (on peut en fait remarquer qu'il s'agit simplement de l'inégalité $(x-y+2)^2 \geq 0$), mais cette méthode peut fonctionner dans des cas plus complexes. Il faudra alors discuter les différents cas selon le signe du discriminant.