Théorie > Géométrie > Angles
Angles orientés
Généralement, on ne considère pas les angles comme étant orientés, en ce sens que les expressions $\widehat{ABC}$ et $\widehat{CBA}$ désignent la même amplitude d'angle, entre $0$ et $\pi$ radians (c'est-à-dire entre $0^\circ$ et $180^\circ$). La plupart du temps sur ce site, et sauf mention contraire, les angles que nous mentionnerons seront en effet non-orientés. Il existe cependant certaines situations dans lesquelles il peut être utile de parler d'angles orientés.
Parler d'angles orientés, c'est décider que les angles $\widehat{ABC}$ et $\widehat{CBA}$ n'auront plus la même amplitude, mais des amplitudes opposées. Pour être plus précis, on commence par se fixer une orientation du plan. Par convention, on oriente le plan dans le sens trigonométrique, c'est-à-dire le sens inverse des aiguilles d'une montre. Une rotation dans le sens trigonométrique sera donc considérée comme positive, alors qu'une rotation dans le sens inverse sera considérée comme négative. À présent, l'amplitude de l'angle orienté $\widehat{ABC}$ est définie comme étant l'angle de la rotation qu'il faut appliquer à la demi-droite $[BA)$ pour l'envoyer sur $[BC)$, en prenant compte du signe de la rotation (selon le sens dans lequel elle s'effectue). Puisqu'une rotation de $2\pi$ (c'est-à-dire $360^\circ$) revient à ne rien tourner, les angles orientés sont définis à un multiple de $2\pi$ près (c'est-à-dire à un multiple de $360^\circ$ près).
La façon la plus simple de comprendre la notion d'angle orienté est de regarder un exemple. Sur la figure suivante, le triangle $ABC$ est équilatéral.
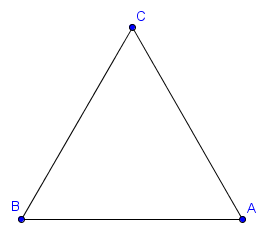
Pour envoyer $[BA)$ sur $[BC)$, on peut appliquer une rotation de $60^\circ$ dans le sens trigonométrique, donc $\widehat{ABC} = 60^\circ$. Cela dit, on peut également appliquer une rotation de $300^\circ$ dans le sens anti-trigonométrique, donc on a aussi $\widehat{ABC} = -300^\circ$. Cela n'est pas dérangeant : les angles $60^\circ$ et $-300^\circ$ sont considérés comme égaux (car égaux à un multiple de $360^\circ$ près). Par contre, l'angle $\widehat{CBA}$ n'a pas une amplitude de $60^\circ$ mais une amplitude de $-60^\circ$, ce qui est aussi égal à $300^\circ$. Lorsqu'on mesure en angles orientés, il faut donc toujours faire bien attention à l'ordre dans lequel on écrit les lettres car les angles $\widehat{ABC}$ et $\widehat{CBA}$ sont considérés comme différents.
On voudra alors, par exemple, utiliser l'égalité évidente $\widehat{ABC} = \widehat{ABD}+\widehat{DBC}$ (en angles non-orientés). Or, cette égalité est certes vraie sur notre figure, mais il existe d'autres configurations pour lesquelles elle n'est plus vraie ! Par exemple, plaçons les quatre points dans l'ordre $A$, $B$, $D$, $C$ comme sur la figure suivante.
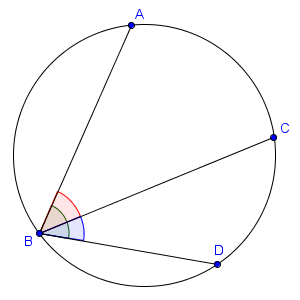
En angles non-orientés, il s'avère que $\widehat{ABC} = \widehat{ABD} - \widehat{DBC}$ (et non plus $\widehat{ABD} + \widehat{DBC}$) ! Si l'on travaille avec des angles non-orientés, il faut donc envisager les deux cas et faire deux raisonnements différents pour résoudre le problème quelle que soit la situation rencontrée ! Cela rend alors les choses deux fois plus longues, d'autant qu'il est probable qu'il faille encore recouper le raisonnement en deux parties plus tard pour les mêmes raisons.
Si par contre on décide de travailler avec des angles orientés (auquel cas il est important de le préciser), alors les choses s'avèrent être plus simples. En effet, en angles orientés, l'égalité $\widehat{ABC} = \widehat{ABD}+\widehat{DBC}$ est correcte quelle que soit la configuration ! Cela vient du fait que $\widehat{CBD} = -\widehat{DBC}$. Il n'est donc pas nécessaire de commencer à discuter différents cas.
Il est toutefois nécessaire, quand plusieurs configurations sont possibles et que l'on décide de travailler avec des angles orientés, de bien vérifier que les angles orientés résolvent le problème des configurations multiples. En effet, il existe des situations pour lesquelles cela ne fonctionne pas. Par exemple, l'égalité $\widehat{ABD} = \widehat{ACD}$ est vraie dans la première figure ci-dessus mais n'est pas correcte dans la deuxième, que les angles soient orientés ou non !
Parler d'angles orientés, c'est décider que les angles $\widehat{ABC}$ et $\widehat{CBA}$ n'auront plus la même amplitude, mais des amplitudes opposées. Pour être plus précis, on commence par se fixer une orientation du plan. Par convention, on oriente le plan dans le sens trigonométrique, c'est-à-dire le sens inverse des aiguilles d'une montre. Une rotation dans le sens trigonométrique sera donc considérée comme positive, alors qu'une rotation dans le sens inverse sera considérée comme négative. À présent, l'amplitude de l'angle orienté $\widehat{ABC}$ est définie comme étant l'angle de la rotation qu'il faut appliquer à la demi-droite $[BA)$ pour l'envoyer sur $[BC)$, en prenant compte du signe de la rotation (selon le sens dans lequel elle s'effectue). Puisqu'une rotation de $2\pi$ (c'est-à-dire $360^\circ$) revient à ne rien tourner, les angles orientés sont définis à un multiple de $2\pi$ près (c'est-à-dire à un multiple de $360^\circ$ près).
La façon la plus simple de comprendre la notion d'angle orienté est de regarder un exemple. Sur la figure suivante, le triangle $ABC$ est équilatéral.

Pour envoyer $[BA)$ sur $[BC)$, on peut appliquer une rotation de $60^\circ$ dans le sens trigonométrique, donc $\widehat{ABC} = 60^\circ$. Cela dit, on peut également appliquer une rotation de $300^\circ$ dans le sens anti-trigonométrique, donc on a aussi $\widehat{ABC} = -300^\circ$. Cela n'est pas dérangeant : les angles $60^\circ$ et $-300^\circ$ sont considérés comme égaux (car égaux à un multiple de $360^\circ$ près). Par contre, l'angle $\widehat{CBA}$ n'a pas une amplitude de $60^\circ$ mais une amplitude de $-60^\circ$, ce qui est aussi égal à $300^\circ$. Lorsqu'on mesure en angles orientés, il faut donc toujours faire bien attention à l'ordre dans lequel on écrit les lettres car les angles $\widehat{ABC}$ et $\widehat{CBA}$ sont considérés comme différents.
Exemple d'utilisation
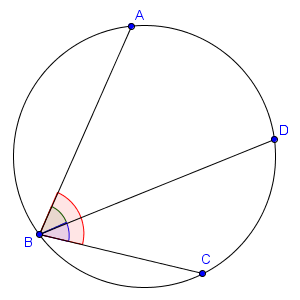
A priori, il semble que décider d'utiliser les angles orientés ne fait que compliquer les choses. Cela dit, il existe des situations dans lesquelles utiliser des angles orientés facilite la vie. Il arrive en effet, dans un problème de géométrie, que la figure prenne des formes différentes selon les choix que l'on effectue au moment de la dessiner. Par exemple, si un énoncé commence par "Soit $A$, $B$, $C$ et $D$ quatres points cocycliques", alors il y a plusieurs façons d'ordonner les quatre points sur le cercle. Disons que, sur notre figure et dans le but de résoudre le problème, on place les quatre points dans l'ordre $A$, $B$, $C$, $D$ comme sur la figure ci-dessous.
On voudra alors, par exemple, utiliser l'égalité évidente $\widehat{ABC} = \widehat{ABD}+\widehat{DBC}$ (en angles non-orientés). Or, cette égalité est certes vraie sur notre figure, mais il existe d'autres configurations pour lesquelles elle n'est plus vraie ! Par exemple, plaçons les quatre points dans l'ordre $A$, $B$, $D$, $C$ comme sur la figure suivante.

En angles non-orientés, il s'avère que $\widehat{ABC} = \widehat{ABD} - \widehat{DBC}$ (et non plus $\widehat{ABD} + \widehat{DBC}$) ! Si l'on travaille avec des angles non-orientés, il faut donc envisager les deux cas et faire deux raisonnements différents pour résoudre le problème quelle que soit la situation rencontrée ! Cela rend alors les choses deux fois plus longues, d'autant qu'il est probable qu'il faille encore recouper le raisonnement en deux parties plus tard pour les mêmes raisons.
Si par contre on décide de travailler avec des angles orientés (auquel cas il est important de le préciser), alors les choses s'avèrent être plus simples. En effet, en angles orientés, l'égalité $\widehat{ABC} = \widehat{ABD}+\widehat{DBC}$ est correcte quelle que soit la configuration ! Cela vient du fait que $\widehat{CBD} = -\widehat{DBC}$. Il n'est donc pas nécessaire de commencer à discuter différents cas.
Il est toutefois nécessaire, quand plusieurs configurations sont possibles et que l'on décide de travailler avec des angles orientés, de bien vérifier que les angles orientés résolvent le problème des configurations multiples. En effet, il existe des situations pour lesquelles cela ne fonctionne pas. Par exemple, l'égalité $\widehat{ABD} = \widehat{ACD}$ est vraie dans la première figure ci-dessus mais n'est pas correcte dans la deuxième, que les angles soient orientés ou non !
Remarque importante
Nous rappelons que, par défaut, toute la théorie, tous les exercices et tous les problèmes sur ce site sont écrits en angles non-orientés. Toutes les amplitudes que nous considérons sont donc à interpréter avec une valeur entre $0$ et $\pi$ (c'est-à-dire entre $0^\circ$ et $180^\circ$), sauf mention explicite du contraire. Pour ces mêmes raisons, un étudiant qui souhaite utiliser les angles orientés dans la résolution d'un problème doit le mentionner explicitement.