Quadrilatères cycliques
Propriétés réciproques
Les deux petites propriétés énoncées dans la section précédente peuvent paraître bien anodines, puisqu'il s'agit juste d'égalités d'angles inscrits. En fait, ce sont surtout leurs réciproques qui sont intéressantes.
Exactement de la même manière, on peut montrer que dans un quadrilatère non cyclique, les angles opposés ne sont jamais supplémentaires.
Par exemple, si l'on constate (après une chasse aux angles) une situation du type $\widehat{ABD} = \widehat{ACD}$ (avec $B$ et $C$ du même côté de $AD$), alors les méthodes simples que nous avions présentées pour chasser les angles ne permet pas de progresser d'avantage. Maintenant que nous connaissons les quadrilatères cycliques, on remarque qu'il est en fait possible de tirer énormément d'informations d'une telle égalité ! En effet, elle signifie que $ABCD$ est cyclique, ce qui nous permet directement de déduire que $\widehat{BCA} = \widehat{BDA}$, $\widehat{CDB} = \widehat{CAB}$, $\widehat{DAC} = \widehat{DBC}$, $\widehat{BAD}+\widehat{BCD} = 180^\circ$ et $\widehat{ABC} + \widehat{ADC} = 180^\circ$. On peut donc, à partir d'une simple égalité d'angles, en déduire $5$ autres ! En pratique, toutes ne sont bien sûr pas utiles, mais il est rare que la découverte d'un quadrilatère cyclique ne soit pas le début d'une avancée majeure dans la résolution d'un problème.
Propriété réciproque 1
Soit $ABCD$ un quadrilatère (non croisé). Si $\widehat{ABD} = \widehat{ACD}$, alors $ABCD$ est cyclique.
Démonstration
La façon la plus intuitive de démontrer ce résultat est de montrer sa contraposée, c'est-à-dire que l'on n'a pas l'égalité d'angles dans un quadrilatère non cyclique.
Considérons dès lors $ABCD$ un quadrilatère non cyclique et montrons que $\widehat{ABD} \neq \widehat{ACD}$. Le cercle $\Gamma$ circonscrit au triangle $ABD$ ne passe donc pas par $C$. On note alors $C'$ l'intersection de $AC$ avec $\Gamma$, et on a $C' \neq C$. Or, le quadrilatère $ABC'D$ est cyclique et nous savons donc qu'on a $\widehat{ABD} = \widehat{AC'D}$. Mais comme $C$ est du même côté de $AD$ que $C'$ (car le quadrilatère n'est pas croisé), on a forcément $\widehat{ACD} \neq \widehat{AC'D}$ et donc $\widehat{ACD} \neq \widehat{ABD}$.
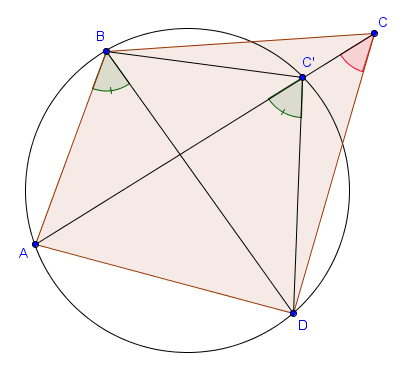
Considérons dès lors $ABCD$ un quadrilatère non cyclique et montrons que $\widehat{ABD} \neq \widehat{ACD}$. Le cercle $\Gamma$ circonscrit au triangle $ABD$ ne passe donc pas par $C$. On note alors $C'$ l'intersection de $AC$ avec $\Gamma$, et on a $C' \neq C$. Or, le quadrilatère $ABC'D$ est cyclique et nous savons donc qu'on a $\widehat{ABD} = \widehat{AC'D}$. Mais comme $C$ est du même côté de $AD$ que $C'$ (car le quadrilatère n'est pas croisé), on a forcément $\widehat{ACD} \neq \widehat{AC'D}$ et donc $\widehat{ACD} \neq \widehat{ABD}$.

Exactement de la même manière, on peut montrer que dans un quadrilatère non cyclique, les angles opposés ne sont jamais supplémentaires.
Propriété réciproque 2
Soit $ABCD$ un quadrilatère (non croisé). Si $\widehat{DAB}+\widehat{BCD}=180^\circ$, alors $ABCD$ est cyclique.
Remarque
Dans les deux propositions précédentes, l'hypothèse comme quoi le quadrilatère doit être non croisé peut être supprimée en utilisant des angles orientés. En effet, l'hypothèse $\widehat{ABD} = \widehat{ACD}$ où les angles sont supposés orientés implique d'elle-même que le quadrilatère est non croisé (car ces deux angles n'ont pas le même signe lorsque $ABCD$ est croisé).
Exemple d'utilisation
Ces résultats peuvent être d'une grande aide dans la résolution de problèmes, et notamment dans une chasse aux angles. En fait, on cherche souvent à trouver un quadrilatère cyclique (alors qu'aucun cercle ne laisse le présager). Pour cela, il suffit de trouver dans la figure qui nous intéresse des angles comme dans l'une des deux propriétés précédentes.Par exemple, si l'on constate (après une chasse aux angles) une situation du type $\widehat{ABD} = \widehat{ACD}$ (avec $B$ et $C$ du même côté de $AD$), alors les méthodes simples que nous avions présentées pour chasser les angles ne permet pas de progresser d'avantage. Maintenant que nous connaissons les quadrilatères cycliques, on remarque qu'il est en fait possible de tirer énormément d'informations d'une telle égalité ! En effet, elle signifie que $ABCD$ est cyclique, ce qui nous permet directement de déduire que $\widehat{BCA} = \widehat{BDA}$, $\widehat{CDB} = \widehat{CAB}$, $\widehat{DAC} = \widehat{DBC}$, $\widehat{BAD}+\widehat{BCD} = 180^\circ$ et $\widehat{ABC} + \widehat{ADC} = 180^\circ$. On peut donc, à partir d'une simple égalité d'angles, en déduire $5$ autres ! En pratique, toutes ne sont bien sûr pas utiles, mais il est rare que la découverte d'un quadrilatère cyclique ne soit pas le début d'une avancée majeure dans la résolution d'un problème.