Théorie > Géométrie > Quadrilatères cycliques
Théorème de Ptolémée
Nous avons vu comment caractériser les quadrilatères cycliques par des relations entre différents angles. Le théorème de Ptolémée permet de donner une condition nécessaire et suffisante sur les longueurs des côtés et des diagonales d'un quadrilatère pour que celui-ci soit cyclique.
Nous ne donnons pas la démonstration du sens $\Leftarrow$ maintenant, elle sera donnée dans un prochain chapitre.
Théorème de Ptolémée
Un quadrilatère (non croisé) $ABCD$ est cyclique si et seulement si
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
Nous ne donnons pas la démonstration du sens $\Leftarrow$ maintenant, elle sera donnée dans un prochain chapitre.
Démonstration du sens $\Rightarrow$
Considérons $ABCD$ un quadrilatère cyclique non-croisé. On note $K$ le point de $[AC]$ tel que $\widehat{ABK} = \widehat{DBC}$.
On a par angles inscrits que $\widehat{CAB} = \widehat{CDB}$, et les triangles $BKA$ et $BCD$ sont dès lors semblables.
Aussi, on a $\widehat{ACB} = \widehat{ADB}$, et puisque $\widehat{KBC} = \widehat{ABD}$ (au vu de notre choix de $K$), les triangles $CBK$ et $DBA$ sont à leur tour semblables.
On déduit de ces deux similitudes que
$$\frac{|KA|}{|BA|} = \frac{|CD|}{|BD|} \ \text{ et } \ \frac{|CK|}{|BC|} = \frac{|DA|}{|BD|},$$ ce qui se réécrit
$$|KA|\cdot|BD| = |CD|\cdot |BA| \ \text{ et } \ |CK| \cdot |BD| = |DA| \cdot |BC|.$$ Il ne reste alors plus qu'à sommer ces deux égalités pour obtenir, comme $|KA| + |CK| = |AC|$ :
$$|AC| \cdot |BD| = |CD| \cdot |BA| + |DA| \cdot |BC|.$$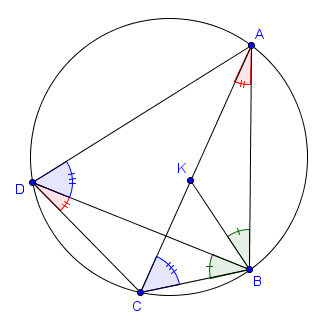
On a par angles inscrits que $\widehat{CAB} = \widehat{CDB}$, et les triangles $BKA$ et $BCD$ sont dès lors semblables.
Aussi, on a $\widehat{ACB} = \widehat{ADB}$, et puisque $\widehat{KBC} = \widehat{ABD}$ (au vu de notre choix de $K$), les triangles $CBK$ et $DBA$ sont à leur tour semblables.
On déduit de ces deux similitudes que
$$\frac{|KA|}{|BA|} = \frac{|CD|}{|BD|} \ \text{ et } \ \frac{|CK|}{|BC|} = \frac{|DA|}{|BD|},$$ ce qui se réécrit
$$|KA|\cdot|BD| = |CD|\cdot |BA| \ \text{ et } \ |CK| \cdot |BD| = |DA| \cdot |BC|.$$ Il ne reste alors plus qu'à sommer ces deux égalités pour obtenir, comme $|KA| + |CK| = |AC|$ :
$$|AC| \cdot |BD| = |CD| \cdot |BA| + |DA| \cdot |BC|.$$
