Théorie > Géométrie > Rapports de section
Définition et propriétés
On commence par définir la notion de rapport orienté entre deux segments parallèles.
Par exemple, dans la figure suivante où $C$, $D$, $E$ et $F$ sont alignés, $AB$ est parallèle à $CF$ et $|CD| = |EF| = 2|DE| = 2|AB|$, on a
$$ \frac{\overline{AB}}{\overline{DE}} = 1, \quad \frac{\overline{CD}}{\overline{FE}} = -1, \quad \frac{\overline{AB}}{\overline{DF}}= \frac{1}{3}, \quad \frac{\overline{CF}}{\overline{BA}} = -5.$$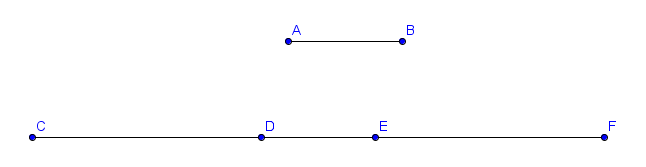
Remarque : Il s'agit bien de rapports, au sens où on a la formule $\displaystyle\frac{\overline{AB}}{\overline{CD}} \cdot \frac{\overline{CD}}{\overline{EF}} = \frac{\overline{AB}}{\overline{EF}}$ lorsque les droites $AB$, $CD$ et $EF$ sont parallèles.
On peut maintenant définir la notion de rapport de section.
On peut par exemple réécrire le théorème de la bissectrice à l'aide des rapports de section. En effet, si dans un triangle $ABC$, $A'$ désigne l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ désigne l'intersection de la bissectrice extérieure de $A$ avec $BC$, le théorème de la bissectrice nous indique que
$$r_{BC}(A') = -\frac{b}{c} \quad \text{ et } \quad r_{BC}(A'') = \frac{b}{c}$$ où $b = |AC|$ et $c = |AB|$.
Il est intéressant de regarder comment $r_{AB}(C)$ varie lorsque $A$ et $B$ sont fixés et que $C$ varie sur la droite $AB$. Ceci est représenté sur le graphique suivant.
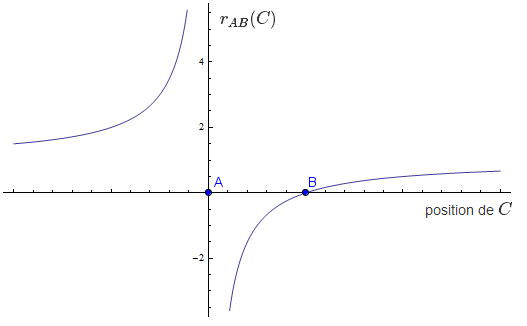
Rapport de section $r_{AB}(C)$ en fonction de la position de $C$.
En fait, il n'est pas compliqué de se convaincre que $r_{AB}(C)$ peut prendre n'importe quelle valeur réelle différente de $1$. Ce qui rend le rapport de section digne d'intérêt est que le rapport de section d'un point par rapport à deux points fixés détermine univoquement la position du point (autrement dit, la fonction tracée ci-dessus est injective). Dès lors, pour montrer que deux points sont égaux, on peut simplement montrer que leurs rapports de section par rapport à deux mêmes points sont égaux.
Définition (rapport orienté)
Soit $A$, $B$, $C$ et $D$ quatre points distincts deux à deux et tels que $AB$ est parallèle à $CD$. Le rapport orienté $\displaystyle \frac{\overline{AB}}{\overline{CD}}$ est défini par
$$ \frac{\overline{AB}}{\overline{CD}} = \left\{\begin{array}{cl}
\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans le même sens,} \\
-\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans des sens opposés.}
\end{array}\right.$$
$$ \frac{\overline{AB}}{\overline{CD}} = \left\{\begin{array}{cl}
\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans le même sens,} \\
-\frac{|AB|}{|CD|} & \text{ si } [AB) \text{ et } [CD) \text{ pointent dans des sens opposés.}
\end{array}\right.$$
Par exemple, dans la figure suivante où $C$, $D$, $E$ et $F$ sont alignés, $AB$ est parallèle à $CF$ et $|CD| = |EF| = 2|DE| = 2|AB|$, on a
$$ \frac{\overline{AB}}{\overline{DE}} = 1, \quad \frac{\overline{CD}}{\overline{FE}} = -1, \quad \frac{\overline{AB}}{\overline{DF}}= \frac{1}{3}, \quad \frac{\overline{CF}}{\overline{BA}} = -5.$$

Remarque : Il s'agit bien de rapports, au sens où on a la formule $\displaystyle\frac{\overline{AB}}{\overline{CD}} \cdot \frac{\overline{CD}}{\overline{EF}} = \frac{\overline{AB}}{\overline{EF}}$ lorsque les droites $AB$, $CD$ et $EF$ sont parallèles.
On peut maintenant définir la notion de rapport de section.
Définition (rapport de section)
Si $C$ est un point de $AB$ distinct de $A$, alors le rapport de section $r_{AB}(C)$ de $C$ par rapport à $A$ et $B$ est défini par
$$r_{AB}(C) = \frac{\overline{CB}}{\overline{CA}}.$$
$$r_{AB}(C) = \frac{\overline{CB}}{\overline{CA}}.$$
On peut par exemple réécrire le théorème de la bissectrice à l'aide des rapports de section. En effet, si dans un triangle $ABC$, $A'$ désigne l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ désigne l'intersection de la bissectrice extérieure de $A$ avec $BC$, le théorème de la bissectrice nous indique que
$$r_{BC}(A') = -\frac{b}{c} \quad \text{ et } \quad r_{BC}(A'') = \frac{b}{c}$$ où $b = |AC|$ et $c = |AB|$.
Il est intéressant de regarder comment $r_{AB}(C)$ varie lorsque $A$ et $B$ sont fixés et que $C$ varie sur la droite $AB$. Ceci est représenté sur le graphique suivant.
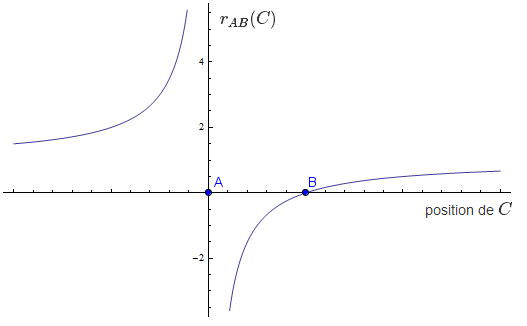
Rapport de section $r_{AB}(C)$ en fonction de la position de $C$.
En fait, il n'est pas compliqué de se convaincre que $r_{AB}(C)$ peut prendre n'importe quelle valeur réelle différente de $1$. Ce qui rend le rapport de section digne d'intérêt est que le rapport de section d'un point par rapport à deux points fixés détermine univoquement la position du point (autrement dit, la fonction tracée ci-dessus est injective). Dès lors, pour montrer que deux points sont égaux, on peut simplement montrer que leurs rapports de section par rapport à deux mêmes points sont égaux.