Triangles (suite)
Relation d'Euler
La relation d'Euler est une égalité ayant lieu dans les triangles. Elle relie le rayon du cercle inscrit, le rayon du cercle circonscrit et la distance entre les centres des cercles inscrits et circonscrits.
Relation d'Euler
Soit $ABC$ un triangle, $R$ le rayon de son cercle circonscrit, $r$ le rayon de son cercle inscrit et $d$ la distance entre les centres des cercles inscrits et circonscrits. Alors
$$d^2 = R(R-2r).$$ En particulier, on a toujours $R \geq 2r$, avec égalité si et seulement si $ABC$ est équilatéral.
$$d^2 = R(R-2r).$$ En particulier, on a toujours $R \geq 2r$, avec égalité si et seulement si $ABC$ est équilatéral.
Démonstration
On note $I$ le centre du cercle inscrit et $O$ celui du cercle circonscrit. On note également $X$ l'intersection de $BI$ avec le cercle circonscrit et $X'$ le point diamétralement opposé à $X$ sur ce cercle. Enfin, on note $D$ le pied de la perpendiculaire à $BC$ passant par $I$.
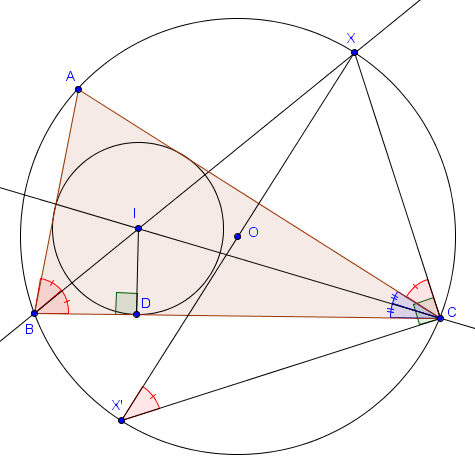
On commence par constater que les triangles $BDI$ et $X'CX$ sont semblables. En effet, ils sont tous les deux rectangles et on a $\widehat{IBD} = \widehat{XBC} = \widehat{XX'C}$ (angles inscrits). On a donc
$$\frac{|ID|}{|IB|} = \frac{|XC|}{|XX'|},$$ c'est-à-dire, puisque $|ID| = r$ et $XX' = 2R$ :
$$|XC| \cdot |IB| = 2Rr.$$ De plus, on a les égalités d'angles
$$\widehat{XIC} = 180^\circ - \widehat{BIC} = \widehat{IBC} + \widehat{ICB} = \frac{\widehat{ABC}+\widehat{ACB}}{2}$$ et
$$\widehat{ICX} = \widehat{ICA}+\widehat{ACX} = \widehat{ICA}+\widehat{ABX} = \frac{\widehat{ABC}+\widehat{ACB}}{2},$$ ce qui signifie que le triangle $IXC$ est isocèle avec $|XI| = |XC|$. La relation trouvée plus haut devient donc
$$|XI|\cdot |IB| = 2Rr.$$ Or, on reconnait en $|XI| \cdot |IB|$ la puissance (au signe près) du point $I$ par rapport au cercle circonscrit. Celle-ci étant, par définition, égale à $d^2-R^2$, on obtient la relation
$$d^2 - R^2 = -2Rr$$ qui est équivalente à la relation d'Euler.
Finalement, on a $0 \leq d^2 = R(R-2r)$ d'où $R \geq 2r$, et l'égalité a lieu si et seulement si $d = 0$, c'est-à-dire si $I = O$. C'est un simple exercice de vérifier que cela n'arrive que lorsque $ABC$ est équilatéral.

On commence par constater que les triangles $BDI$ et $X'CX$ sont semblables. En effet, ils sont tous les deux rectangles et on a $\widehat{IBD} = \widehat{XBC} = \widehat{XX'C}$ (angles inscrits). On a donc
$$\frac{|ID|}{|IB|} = \frac{|XC|}{|XX'|},$$ c'est-à-dire, puisque $|ID| = r$ et $XX' = 2R$ :
$$|XC| \cdot |IB| = 2Rr.$$ De plus, on a les égalités d'angles
$$\widehat{XIC} = 180^\circ - \widehat{BIC} = \widehat{IBC} + \widehat{ICB} = \frac{\widehat{ABC}+\widehat{ACB}}{2}$$ et
$$\widehat{ICX} = \widehat{ICA}+\widehat{ACX} = \widehat{ICA}+\widehat{ABX} = \frac{\widehat{ABC}+\widehat{ACB}}{2},$$ ce qui signifie que le triangle $IXC$ est isocèle avec $|XI| = |XC|$. La relation trouvée plus haut devient donc
$$|XI|\cdot |IB| = 2Rr.$$ Or, on reconnait en $|XI| \cdot |IB|$ la puissance (au signe près) du point $I$ par rapport au cercle circonscrit. Celle-ci étant, par définition, égale à $d^2-R^2$, on obtient la relation
$$d^2 - R^2 = -2Rr$$ qui est équivalente à la relation d'Euler.
Finalement, on a $0 \leq d^2 = R(R-2r)$ d'où $R \geq 2r$, et l'égalité a lieu si et seulement si $d = 0$, c'est-à-dire si $I = O$. C'est un simple exercice de vérifier que cela n'arrive que lorsque $ABC$ est équilatéral.