Invariants et (mono)variants
Invariants
Les invariants permettent de résoudre des problèmes dans lesquels une tâche, une opération ou une transformation est répétée un certain nombre de fois (éventuellement une infinité). Un invariant est, dans une telle situation, une quantité qui ne varie pas lors de la transformation. Pour bien comprendre comment ceux-ci fonctionnent, examinons deux exemples différents.
Ce raisonnement, bien qu'achevant le problème, n'est pas très joli et peut très vite être erroné. De plus, il fonctionne ici car il n'y a que six secteurs, mais il aurait par exemple été bien plus difficile à appliquer s'il y avait eu $2014$ secteurs. En fait, il était possible de résoudre le problème très rapidement en utilisant un invariant.
Le problème suivant est un autre exemple où un invariant permet de conclure directement :
Problème
Un cercle est divisé en $6$ secteurs. Quatre d'entre eux contiennent le nombre $0$ et les deux autres le nombre $1$, de la manière indiquée sur la figure suivante. On peut augmenter de une unité le contenu de deux cases voisines. Peut-on atteindre un état où les contenus des cases sont tous égaux ?
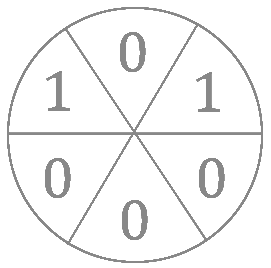

Solution fastidieuse
Pour résoudre un tel problème, on commence bien sûr par essayer d'obtenir six nombres égaux. Il ne faut que peu de temps pour se convaincre que cela est en fait impossible. L'approche la plus intuitive pour résoudre ce problème est peut-être la suivante. On observe tout d'abord qu'il n'y a que six opérations possibles (il n'y a que six choix différents de deux cases voisines), et que l'ordre dans lequel on effectue les opérations n'a aucune importance. On peut alors procéder par l'absurde et supposer qu'il existe une suite d'opérations amenant à un état où les six nombres sont égaux. On numérote $1, \ldots, 6$ les six secteurs (de sorte que les secteurs $1$ et $3$ contiennent le chiffre $1$) et on note $n_1$ le nombre de fois que l'on a incrémenté les cases $1$ et $2$, $n_2$ le nombre de fois que l'on a incrémenté les cases $2$ et $3$, et ainsi de suite jusque $n_6$, le nombre de fois que l'on a incrémenté les cases $6$ et $1$. Le fait que les six valeurs sont égales après ces opérations s'écrit alors
$$1+n_6+n_1 = n_1+n_2 = 1+n_2+n_3 = n_3+n_4 = n_4+n_5 = n_5+n_6.$$ Il ne reste alors plus qu'à trouver une absurdité pour conclure que c'est impossible. En fait, on peut par exemple remarquer que certaines de ces égalités impliquent
$$n_6+1 = n_2,$$ $$n_2+1 = n_4,$$ $$n_4 = n_6,$$ ce qui est impossible (en additionnant les trois égalités, on trouve $2 = 0$).
$$1+n_6+n_1 = n_1+n_2 = 1+n_2+n_3 = n_3+n_4 = n_4+n_5 = n_5+n_6.$$ Il ne reste alors plus qu'à trouver une absurdité pour conclure que c'est impossible. En fait, on peut par exemple remarquer que certaines de ces égalités impliquent
$$n_6+1 = n_2,$$ $$n_2+1 = n_4,$$ $$n_4 = n_6,$$ ce qui est impossible (en additionnant les trois égalités, on trouve $2 = 0$).
Ce raisonnement, bien qu'achevant le problème, n'est pas très joli et peut très vite être erroné. De plus, il fonctionne ici car il n'y a que six secteurs, mais il aurait par exemple été bien plus difficile à appliquer s'il y avait eu $2014$ secteurs. En fait, il était possible de résoudre le problème très rapidement en utilisant un invariant.
Solution avec un invariant
L'idée est de noter $x_1, \ldots, x_6$ les valeurs des nombres dans les six secteurs (disons avec $x_1 = x_3 = 1$ au départ), et de trouver une fonction de ces $x_1, \ldots, x_6$ ayant la propriété qu'elle ne change pas lorsqu'on effectue une opération. Les opérations consistant à incrémenter les valeurs de deux $x_i$ consécutifs, l'invariant le plus naturel est
$$X = x_1 - x_2 + x_3 - x_4 + x_5 - x_6.$$ En effet, à chaque fois que l'on augmente $x_i$ et $x_{i+1}$ pour un certain $i$ (ou $x_6$ et $x_1$), la valeur de $X$ ne change pas. Il s'agit donc bien d'un invariant du problème. Il reste alors à constater que $X = 2$ dans la configuration initiale, ce qui signifie que quelles que soient les opérations que l'on effectue sur nos secteurs, la valeur de $X$ restera toujours égale à $2$. Or, nous nous demandons s'il est possible d'atteindre un état où $x_1 = \ldots = x_6$. Dans un tel état, la valeur de $X$ est égale à $0$, donc nous venons de montrer qu'on ne parviendra jamais à égaliser les six nombres.
$$X = x_1 - x_2 + x_3 - x_4 + x_5 - x_6.$$ En effet, à chaque fois que l'on augmente $x_i$ et $x_{i+1}$ pour un certain $i$ (ou $x_6$ et $x_1$), la valeur de $X$ ne change pas. Il s'agit donc bien d'un invariant du problème. Il reste alors à constater que $X = 2$ dans la configuration initiale, ce qui signifie que quelles que soient les opérations que l'on effectue sur nos secteurs, la valeur de $X$ restera toujours égale à $2$. Or, nous nous demandons s'il est possible d'atteindre un état où $x_1 = \ldots = x_6$. Dans un tel état, la valeur de $X$ est égale à $0$, donc nous venons de montrer qu'on ne parviendra jamais à égaliser les six nombres.
Le problème suivant est un autre exemple où un invariant permet de conclure directement :
Problème
Les nombres $1, 2, \ldots, 1974$ sont écrits sur un tableau. On peut remplacer deux quelconques de ces nombres par leur somme ou par leur différence. Peut-on obtenir le nombre $0$ après avoir répété cette opération $1973$ fois ?
Solution
Vu qu'une opération consiste à remplacer deux nombres par leur somme, un invariant envisageable est
$$X = \text{somme des éléments écrits sur le tableau.}$$ Bien sûr, lorsque l'on remplace deux éléments par leur somme, la valeur de $X$ ne change pas. Malheureusement, ce n'est pas le cas lorsque l'on remplace deux éléments par leur différence. En effet, si on remplace les deux nombres $a$ et $b$ (avec $a \geq b$) par leur différence $(a-b)$, la valeur de $X$ diminue de $a+b-(a-b) = 2b$. On constate cependant par ce calcul que $2b$ est toujours pair, ce qui signifie que la valeur de $X$, même si elle change, ne changera jamais de parité ! On peut donc remplacer notre invariant potentiel $X$ par
$$Y = \text{parité de la somme des éléments écrits sur le tableau.}$$ Nous avons montré que $Y$ était bel et bien un invariant du problème. Or, au départ, la somme des éléments est égale à
$$1+2+\ldots+1974 = \frac{1974\cdot1975}{2} = 987 \cdot 1975,$$ ce qui signifie que la valeur de $Y$ est "impair" dans la configuration initiale. Après $1973$ opérations, le nombre que l'on obtiendra sur le tableau sera donc toujours impair, ce qui signifie qu'il ne pourra jamais être nul.
$$X = \text{somme des éléments écrits sur le tableau.}$$ Bien sûr, lorsque l'on remplace deux éléments par leur somme, la valeur de $X$ ne change pas. Malheureusement, ce n'est pas le cas lorsque l'on remplace deux éléments par leur différence. En effet, si on remplace les deux nombres $a$ et $b$ (avec $a \geq b$) par leur différence $(a-b)$, la valeur de $X$ diminue de $a+b-(a-b) = 2b$. On constate cependant par ce calcul que $2b$ est toujours pair, ce qui signifie que la valeur de $X$, même si elle change, ne changera jamais de parité ! On peut donc remplacer notre invariant potentiel $X$ par
$$Y = \text{parité de la somme des éléments écrits sur le tableau.}$$ Nous avons montré que $Y$ était bel et bien un invariant du problème. Or, au départ, la somme des éléments est égale à
$$1+2+\ldots+1974 = \frac{1974\cdot1975}{2} = 987 \cdot 1975,$$ ce qui signifie que la valeur de $Y$ est "impair" dans la configuration initiale. Après $1973$ opérations, le nombre que l'on obtiendra sur le tableau sera donc toujours impair, ce qui signifie qu'il ne pourra jamais être nul.