Théorie des graphes
Graphes planaires
Énigme des trois maisons
L'énigme des trois maisons consiste à résoudre le problème suivant.Énigme des trois maisons
On a trois maisons (numérotées $1$, $2$ et $3$), représentées en bas de la figure suivante, et trois usines, représentées en haut. La première usine fournit de l'eau, la deuxième du gaz et la troisième de l'électricité. On désire relier chacune des trois maisons aux trois usines pour qu'elles aient accès à l'eau, au gaz et à l'électricité. Une contrainte supplémentaire est que les tuyaux ne doivent jamais se croiser.


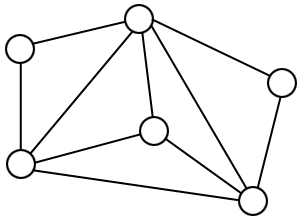
Ce problème peut se réécrire en termes de théorie des graphes. On a déjà les six sommets, et on cherche à relier chaque sommet du bas à chaque sommet du haut par une arête, de sorte qu'aucune arête n'en croise une autre. On définit alors un graphe planaire comme étant un graphe qui peut être représenté dans le plan sans qu'aucune arête n'en croise une autre. Par exemple, le graphe suivant est planaire :
L'énigme des trois maisons consiste alors à représenter le graphe suivant, noté $K_{3,3}$, sans qu'aucune arête ne croise une autre, pourvu bien sûr que ce soit faisable, c'est-à-dire qu'il soit planaire.
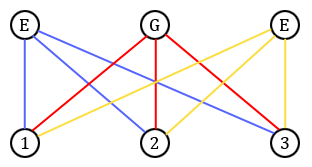
Après plusieurs essais (essayez !), il semble difficile de résoudre cette énigme. Serait-il possible que ce graphe ne soit pas planaire et qu'il n'existe donc pas de solution à l'énigme ? Pour le voir, nous aurons besoin de la formule d'Euler.
Formule d'Euler
La formule d'Euler est une relation entre le nombre de sommets, le nombre d'arêtes et le nombre de faces d'un graphe connexe planaire. Une face d'un graphe planaire est simplement une zone du plan délimitée par des arêtes. Lorsqu'on compte le nombre de faces d'un graphe planaire, il ne faut pas oublier la face extérieure (celle qui est infinie). Sur l'exemple de graphe planaire donné plus haut, on a $6$ sommets, $10$ arêtes et $6$ faces.Formule d'Euler
Dans un graphe planaire connexe, on a toujours
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du graphe.
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du graphe.
Cette formule est bien vérifiée sur notre exemple puisque $6-10+6 = 2$.
Démonstration
Un graphe connexe peut être obtenu en partant du graphe avec un seul sommet et aucune arête et en rajoutant des arêtes une par une, partant d'un sommet déjà existant et arrivant vers un sommet soit déjà existant, soit nouveau. Au départ, on a $1$ sommet, $0$ arête et $1$ faces, et la relation $1-0+1 = 2$ est bien vérifiée. Il suffit donc de montrer qu'à chaque fois que l'on rajoute une arête (et éventuellement le sommet d'arrivée avec s'il n'existait pas encore), la valeur de $s-a+f$ reste inchangée. Deux cas de figure se présentent lorsqu'on rajoute une arête :
- Si le sommet d'arrivée de l'arête n'existe pas encore, alors on le rajoute en même temps que l'arête. En rajoutant cette arête et ce sommet, le nombre de faces reste inchangé (puisque la nouvelle arête ne coupe aucune face en deux). On a donc $s$ qui devient $(s+1)$ et $a$ qui devient $(a+1)$, et la valeur de $s-a+f$ ne change pas.
- Si le sommet d'arrivée de l'arête existe déjà, alors on ne rajoute aucun sommet. Par contre, la nouvelle arête coupe toujours une face en deux. Dans ce cas, $a$ devient donc $(a+1)$ et $f$ devient $(f+1)$, ce qui laisse à nouveau la valeur de $s-a+f$ inchangée.
On peut utiliser la formule d'Euler pour montrer que le graphe $K_{3,3}$ n'est pas planaire, c'est-à-dire que l'énigme des trois maisons ne possède en fait pas de solution.
Théorème (solution de l'énigme des trois maisons)
Le graphe $K_{3,3}$ n'est pas planaire.
Démonstration
Supposons par l'absurde que le graphe $K_{3,3}$ est planaire. Celui-ci possède $s = 6$ sommets et $a = 9$ arêtes, et la formule d'Euler nous dit que le nombre de faces est forcément égal à
$$f = 2-s+a = 2-6+9 = 5.$$ Or, chaque face possède au moins $4$ arêtes. En effet, il n'est pas possible d'avoir une face avec $3$ arêtes puisqu'une arête relie toujours un sommet du bas à un sommet du haut (et pour avoir un cycle, il faut donc un nombre pair d'arêtes). Puisque chaque arête intervient dans exactement deux faces différentes, on ne peut, avec $9$ arêtes, qu'avoir au plus
$$\frac{9}{4} \cdot 2 = 4,\!5 \text{ faces}.$$ On arrive donc à une contradiction puisque $4,\!5 < 5$.
$$f = 2-s+a = 2-6+9 = 5.$$ Or, chaque face possède au moins $4$ arêtes. En effet, il n'est pas possible d'avoir une face avec $3$ arêtes puisqu'une arête relie toujours un sommet du bas à un sommet du haut (et pour avoir un cycle, il faut donc un nombre pair d'arêtes). Puisque chaque arête intervient dans exactement deux faces différentes, on ne peut, avec $9$ arêtes, qu'avoir au plus
$$\frac{9}{4} \cdot 2 = 4,\!5 \text{ faces}.$$ On arrive donc à une contradiction puisque $4,\!5 < 5$.
Formule d'Euler pour les polyèdres
La formule d'Euler est également vraie pour les polyèdres convexes. Cela peut sembler être un hasard, mais il est en fait possible de passer d'un polyèdre à un graphe planaire avec un peu d'astuce.Formule d'Euler pour les polyèdres
Dans un polyèdre convexe dans l'espace, on a toujours
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du polyèdre.
$$s-a+f = 2,$$ où $s$ représente le nombre de sommets, $a$ le nombre d'arêtes et $f$ le nombre de faces du polyèdre.
Idée de la démonstration
Il suffit en fait, à partir d'un polyèdre convexe, de construire un graphe planaire avec le même nombre d'arêtes, de sommets et de faces. L'idée est en fait assez simple. Considérons un certain polyèdre convexe. Pour construire un graphe planaire, on peut simplement poser le polyèdre sur une surface plane, "percer un trou" au milieu d'une des faces du polyèdre (de préférence une face en haut) et élargir ce trou jusqu'à "déplier" le polyèdre et l'aplatir sur la surface plane. On obtient ainsi un graphe planaire avec exactement le même nombre de sommets, d'arêtes et de faces, et on peut utiliser la formule d'Euler pour les graphes planaires. Notez que la face "percée" devient la face infinie du graphe.
Il s'agit là de l'intuition de la démonstration, mais celle-ci peut en fait être facilement rendue rigoureuse. Nous ne le faisons pas ici car cela demande la connaissance de la projection stéréographique.