Nombres complexes (forme exponentielle)
Forme exponentielle
Propriété de l'argument
La forme trigonométrique des nombres complexes peut sembler peu pratique. En effet, si $z = r(\cos \theta + i \sin \theta)$ et $z' = r'(\cos\theta' + i\sin \theta')$, alors il ne semble pas évident de trouver la forme trigonométrique de $z+z'$. On a bien$$z + z' = (r \cos \theta + r' \cos \theta') + i(r \sin \theta + r' \sin \theta'),$$ et on peut calculer le module et l'argument de cette somme, mais il ne s'agira pas d'une formule intéressante.
En fait, la forme trigonométrique se révèle très pratique lorsqu'on désire multiplier des nombres complexes. Si on a $z = r(\cos \theta + i \sin \theta)$ et $z' = r'(\cos\theta' + i\sin \theta')$, on trouve effectivement
$$\begin{align}
z\cdot z' &= r(\cos \theta + i \sin \theta)\cdot r'(\cos \theta' + i \sin \theta') \\
&= rr'\left(\cos\theta \cos \theta' - \sin \theta \sin \theta' + i(\cos \theta \sin \theta' + \sin \theta \cos \theta')\right) \\
&= rr'\left(\cos(\theta+\theta') + i \sin (\theta + \theta') \right)
\end{align}$$ On trouve directement la forme trigonométrique du produit de $z$ et $z'$ ! Son module est $rr'$ et son argument $\theta+\theta'$, ce qui signifie que le module d'un produit est égal au produit des modules (nous avions déjà donné cette propriété) et que l'argument d'un produit est égal à la somme des arguments :
$$\arg(z \cdot z') = \arg z + \arg z'.$$
Forme exponentielle des nombres complexes
La dernière formule trouvée pour l'argument d'un produit n'est pas sans rappeler les exponentielles, puisque le produit de deux exponentielles est égal à l'exponentielle de la somme. C'est pour cette raison que l'on introduit la notation suivante :$$e^{i \theta} = \cos \theta + i \sin \theta.$$ Il ne faut pas ici s'effrayer face à l'exponentielle : il ne s'agit que d'une notation. Historiquement, cette dernière égalité est en fait plutôt connue comme la formule d'Euler. En effet, il est possible de définir une exponentielle complexe $e^{ix}$ d'une façon totalement indépendante des fonctions trigonométriques, et la formule d'Euler donne alors une relation étonnante entre l'exponentielle et les fonctions trigonométriques. Cela n'est cependant pas notre point de vue, et il faut juste retenir qu'il s'agit d'une nouvelle notation.
Un cas particulier de la formule d'Euler est l'identité d'Euler bien connue suivante :
$$e^{i\pi} + 1 = 0$$ Encore une fois, cette identité peut sembler bien anodine au vu de notre définition de $e^{i \theta}$ comme une notation, mais il y a derrière elle quelque chose de bien plus fondamental. Cette identité est impressionnante de par le fait qu'elle relie les valeurs fondamentales $e$, $i$ et $\pi$ a priori indépendantes à l'aide des trois opérations arithmétiques d'addition, multiplication et exponentiation.
Au vu de la forme trigonométrique, on peut maintenant écrire un nombre complexe de module $r$ et d'agument $\theta$ comme
$$z = r \cdot e^{i \theta}.$$ Pour reprendre l'exemple donné précédemment, on a $\sqrt{3}-i = 2\cdot e^{-i\frac{\pi}{6}}$.
Multiplication sous forme exponentielle
Alors que multiplier deux nombres complexes sous la forme usuelle donnait lieu à des formules compliquées, la multiplication est un jeu d'enfant sous la forme exponentielle. On a en effet$$\left(r \cdot e^{i \theta}\right)\cdot \left(r' \cdot e^{i \theta'}\right) = rr' \cdot e^{i(\theta + \theta')}.$$ Cette formule nous donne aussi directement l'inverse d'un nombre complexe $r \cdot e^{i \theta}$, puisqu'il faut avoir $rr' = 1$ et $\theta+\theta' = 0$. On a ainsi
$$\frac{1}{r \cdot e^{i \theta}} = \frac{1}{r} \cdot e^{-i\theta}.$$ On peut maintenant voir comment, sur le plan complexe, on peut construire le produit de deux nombres complexes. Pour effectuer la somme de $z$ et $z'$, il suffit de prendre la somme des vecteurs $\vec{OZ}$ et $\vec{OZ'}$ où $Z$ et $Z'$ sont les points du plan représentant $z$ et $z'$. L'interprétation est un peu plus compliquée pour le produit. On note $U$ le point de coordonnées $(1,0)$, c'est-à-dire celui associé au nombre complexe $1$. Alors le point $P$ correspondant au produit de $z$ et $z'$ est tel que les triangles $OZ'P$ et $OUZ$ sont semblables, comme sur la figure suivante.
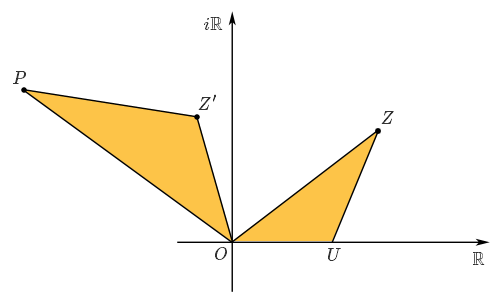
En effet, puisque $\arg(z\cdot z') = \arg z + \arg z'$, on a $\widehat{UOP} = \widehat{UOZ} + \widehat{UOZ'}$, d'où on déduit $\widehat{Z'OP} = \widehat{UOZ}$. Les deux triangles sont alors semblables puisqu'on a également
$$\frac{|OP|}{|OZ'|} = \frac{|z \cdot z'|}{|z'|} = |z| = \frac{|z|}{|1|} = \frac{|OZ|}{|OU|}.$$
Multiplier par $r \cdot e^{i \theta}$ revient en fait à effectuer une rotation d'angle $\theta$ ainsi qu'une homothétie de rapport $r$ (avec l'origine pour centre).