Rapports anharmoniques
Théorème de Desargues
Le théorème de Desargues peut également se démontrer via les rapports anharmoniques :
On retiendra surtout de cette preuve que calculer le rapport anharmonique de quatre droites concourantes en considérant deux sécantes différentes peut souvent se révéler utile. Aussi, les rapports anharmoniques constituent clairement un outil puissant permettant de montrer que trois droites sont concourantes ou que trois points sont alignés. Les preuves des théorèmes de Pascal, Pappus et Desargues en sont de bons exemples.
Théorème de Desargues
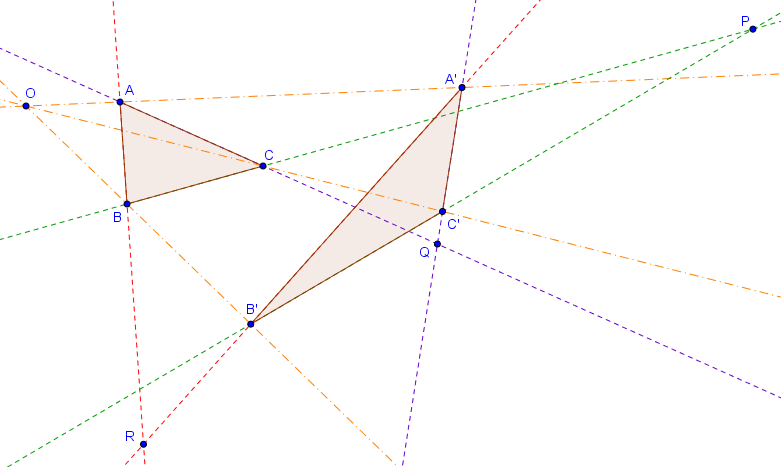
Soit $ABC$ et $A'B'C'$ deux triangles. Supposons que $BC$ et $B'C'$ s'intersectent en $P$, que $AC$ et $A'C'$ s'intersectent en $Q$, et que $AB$ et $A'B'$ s'intersectent en $R$. Alors les points $P, Q, R$ sont alignés si et seulement si les droites $AA'$, $BB'$ et $CC'$ sont concourantes ou parallèles.

Démonstration
Pour plus de simplicité nous supposerons que les droites en considération ne sont jamais parallèles.
- Supposons dans un premier temps que $AA'$, $BB'$ et $CC'$ sont concourantes en un point $O$. On désire montrer que $P$, $Q$ et $R$ sont alignés.
On calcule le rapport anharmonique des droites $RA$, $RA'$, $RO$ et $RQ$ de deux manières différentes, en considérant les sécantes $AA'$ et $BB'$. On trouve :
$$(A,A';O,AA' \cap RQ) = (RA, RA'; RO, RQ) = (B,B';O, BB' \cap RQ).$$ De façon similaire, on calcule le rapport anharmonique des droites $QA$, $QA'$, $QO$ et $QR$ de deux manières différentes, en considérant les sécantes $AA'$ et $CC'$ :
$$(A,A';O,AA'\cap QR) = (QA, QA'; QO, QR) = (C,C';O, CC' \cap QR).$$ On déduit des deux égalités précédentes que
$$(B,B';O, BB' \cap RQ) = (C,C';O, CC' \cap QR).$$ Le point $O$ étant commun à ces deux rapports anharmoniques, on en déduit que les droites $BC$, $B'C'$ et $JK$ sont concourantes, où $J = BB' \cap QR$ et $K = CC' \cap QR$. Clairement $JK = QR$, et comme l'intersection de $BC$ et $B'C'$ est $P$ par définition, on en déduit que $P$ se situe sur $QR$, comme voulu. - Nous montrons maintenant la réciproque. On suppose que $P, Q, R$ sont alignés, et on désire prouver que $AA'$, $BB'$ et $CC'$ sont concourantes. Nous désignons par $O$ l'intersection de $AA'$ et $BB'$, et notre but est de montrer que $CC'$ passe par $O$.
Comme ci-dessus, on a l'égalité
$$(A,A';O,AA' \cap RQ) = (RA, RA'; RO, RQ) = (B,B';O, BB' \cap RQ).$$ D'autre part, si on calcule le rapport anharmonique des droites $QA$, $QA'$, $QO$ et $QR$ à partir des sécantes $AA'$ et $CO$, on obtient
$$(A,A';O,AA'\cap QR) = (QA, QA'; QO, QR) = (C,CO \cap QA';O, CO \cap QR).$$ Finalement, le rapport anharmonique des droites $PB$, $PB'$, $PO$ et $PQ$ se calcule à partir des sécantes $BB'$ et $CO$ et on trouve
$$(B,B';O,BB' \cap PQ) = (PB,PB';PO,PQ) = (C,CO \cap PB'; O, CO \cap PQ).$$ En utilisant les trois égalités précédentes, on obtient que
$$(C,CO \cap QA';O, CO \cap QR) = (C,CO \cap PB'; O, CO \cap PQ),$$ ce qui signifie que $CO \cap QA' = CO \cap PB'$. Les droites $CO$, $QA'$ et $PB'$ sont donc concourantes. Mais $QA' \cap PB' = C'$, donc cela signifie que $CO$ passe par $C'$. Par conséquent, $C$, $C'$ et $O$ sont alignés comme espéré.
On retiendra surtout de cette preuve que calculer le rapport anharmonique de quatre droites concourantes en considérant deux sécantes différentes peut souvent se révéler utile. Aussi, les rapports anharmoniques constituent clairement un outil puissant permettant de montrer que trois droites sont concourantes ou que trois points sont alignés. Les preuves des théorèmes de Pascal, Pappus et Desargues en sont de bons exemples.