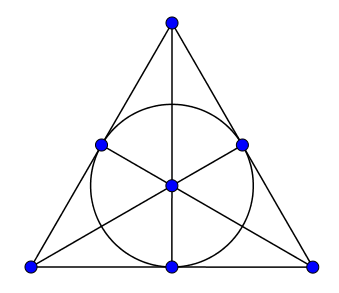
Définition
Un plan projectif est la donnée d'un ensemble $\mathcal{P}$ (dont les éléments sont appelés points), d'un ensemble $\mathcal{L}$ (dont les éléments sont appelés droites) et d'un sous-ensemble $R \subseteq \mathcal{P} \times \mathcal{L}$ satisfaisant les trois propriétés ci-dessous. On dit que la droite $\ell \in \mathcal{L}$ passe par le point $p \in \mathcal{P}$ (et que $p$ appartient à $\ell$) lorsque $(p,\ell) \in R$. L'ensemble $R$ encode donc quels points se situent sur quelles droites.- Pour tous points $p_1 \neq p_2 \in \mathcal{P}$, il existe une unique droite $\ell \in \mathcal{L}$ passant par $p_1$ et $p_2$.
- Pour toutes droites $\ell_1 \neq \ell_2 \in \mathcal{L}$, il existe un unique point $p \in \mathcal{P}$ appartenant à $\ell_1$ et $\ell_2$.
- Il existe quatre points trois à trois non alignés (c'est-à-dire tels qu'aucune droite ne passe par trois d'entre eux).
Plans projectifs finis
Le plan projectif réel, défini dans le nouveau chapitre, est infini au sens où il possède une infinité de points et une infinité de droites. Au contraire, nous nous intéressons ici aux plans projectifs finis, c'est-à-dire ceux où $\mathcal{P}$ et $\mathcal{L}$ sont finis. (À noter que si $\mathcal{P}$ est fini, alors $\mathcal{L}$ aussi, et vice versa.) En utilisant les axiomes des plans projectifs, on peut aisément montrer le fait suivant. (Pour ceux qui le désirent, c'est un bon exercice !)Soit $\Pi = (\mathcal{P}, \mathcal{L}, R)$ un plan projectif fini. Alors il existe un nombre entier $q \geq 2$, appelé l'ordre de $\Pi$, tel que :
- tout point de $\Pi$ appartient à exactement $q+1$ droites;
- toute droite de $\Pi$ passe par exactement $q+1$ points;
- $\Pi$ contient exactement $|\mathcal{P}| = q^2+q+1$ points;
- $\Pi$ contient exactement $|\mathcal{L}| = q^2+q+1$ droites.
Jeu Dobble
Le jeu Dobble est bien connu, et derrière ce jeu se cache en fait un plan projectif ! En effet, le jeu consiste en différentes cartes sur lesquelles sont dessinés $8$ symboles, et est tel que deux cartes possèdent toujours un unique symbole commun. On y voit facilement l'analogie avec les plans projectifs : les cartes peuvent être vues comme des droites, et les symboles comme des points. Il existe un plan projectif d'ordre $7$, ce qui signifie qu'on peu construire un jeu de $7^2+7+1=57$ cartes contenant chacune $7+1=8$ symboles (parmi $57$ symboles au total) tel que deux cartes ont toujours un unique symbole en commun. Par la propriété des plans projectifs, on sait aussi que pour toute paire de symboles, il existe une unique carte contenant ceux-ci (mais ça n'a pas d'intérêt pour le jeu). Malheureusement le vrai jeu Dobble n'est pas totalement satisfaisant, puisqu'il contient bien $57$ symboles mais ne contient que $55$ cartes ! Il y a donc deux cartes manquantes au jeu pour qu'il soit réellement un plan projectif d'ordre $7$. Si vous avez un jeu Dobble chez vous et un peu de temps à perdre, vous pouvez vous amuser à recomposer les deux cartes manquantes (en trouvant les symboles qu'elles doivent contenir).Conjecture
La conjecture suivante est très ancienne, très facile à exprimer et il y a pourtant très peu de progrès dessus :Conjecture : Soit $\Pi$ un plan projectif d'ordre $q$. Alors $q$ est une puissance d'un nombre premier.
Il a pu être vérifié qu'il n'existe aucun plan projectif d'ordre $6$ ou d'ordre $10$, mais on ne sait par exemple pas s'il existe un plan projectif d'ordre $12$ ! Autrement dit, on ignore s'il existe un jeu Dobble avec $12^2+12+1=157$ cartes et $157$ symboles, où chaque carte contient $12+1=13$ symboles et deux cartes ont toujours un unique symbole en commun. (Il n'est pas nécessaire ici de demander les propriétés 1 et 3 des plans projectifs : ce sont en fait des conséquences des hypothèses précédentes.)
La seule réponse partielle à cette conjecture est la suivante :
Théorème de Bruck-Ryser (1949) : S'il existe un plan projectif d'ordre $q$ avec $q \equiv 1 \text{ ou } 2 \pmod 4$, alors $q$ est la somme de deux carrés parfaits.
Ce théorème exclut par exemple les plans projectifs d'ordre $14$. Notez par contre que $2018 = 13^2+43^2$, donc le théorème ne s'applique pas à $q = 2018$. La question en titre de cette actualité n'a donc pas de réponse à ce jour : on ignore s'il existe un plan projectif d'ordre $2018$.
Que ceux que ça intéresse n'hésitent pas à plancher sur la conjecture et à remercier Mathraining au moment de la remise de la médaille Fields ! Bonne année 2018 !