Théorie > Inégalités > Boîte à outils des inégalités
Transformation de Ravi
La transformation de Ravi est à nouveau un changement de variables pouvant être effectué sous certaines conditions.
Celle-ci peut en fait être appliquée lorsque l'on est en présence de trois variables $a$, $b$ et $c$ positives dont on sait qu'elles correspondent aux longueurs des trois côtés d'un même triangle, c'est-à-dire qu'elles vérifient les inégalités
$$\begin{align}
a + b & \geq c,\\[1mm]
b + c & \geq a,\\[1mm]
c + a & \geq b.
\end{align}$$ En pratique, cette condition est généralement énoncée telle quelle dans l'énoncé du problème : celui-ci commence par exemple par "Montrer que si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle, alors ils vérifient l'inégalité suivante".
La transformation de Ravi consiste alors à remplacer $a$, $b$ et $c$ par $x$, $y$ et $z$ (positifs) en effectuant le changement de variable
$$\left\{\begin{align}
a & = y+z \\[1mm]
b &= z + x \\[1mm]
c &= x + y
\end{align}\right.$$ ce qui revient en fait à poser
$$\left\{\begin{align}
x & = \frac{b + c - a}{2} \\[2mm]
y & = \frac{c + a - b}{2} \\[2mm]
z & = \frac{a + b - c}{2}
\end{align}\right.$$
Il existe une façon géométrique de visualiser ce changement de variables. En effet, si on dessine le triangle dont les longueurs des côtés sont $a$, $b$ et $c$, alors les valeurs de $x$, $y$ et $z$ peuvent être trouvées en traçant le cercle inscrit au triangle et évaluant les distances des points de tangence aux différents sommets, comme illustré sur la figure suivante.
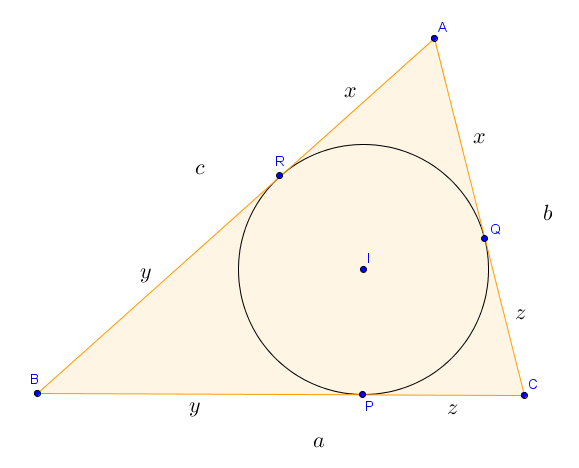
Sur cette figure, on a $a = |BC|$, $b = |AC|$ et $c = |AB|$. De plus, on a les égalités de longueurs $|AQ| = |AR| = x$, $|BP| = |BR| = y$ et $|CP| = |CQ| = z$ car les triangles $AQI$ et $ARI$ sont isométriques, tout comme les triangles $BPI$ et $BRI$ et les triangles $CPI$ et $CQI$.
Cette transformation est d'une grande utilité lorsque les variables $a$, $b$ et $c$ sont supposées être les longueurs d'un triangle. En effet, elle permet de passer à une inégalité en $a$, $b$ et $c$ sous cette contrainte (qu'il ne semble a priori pas évident d'utiliser) à une inégalité équivalente en $x$, $y$ et $z$ sans contrainte. En effet, il n'y a plus aucune contrainte sur $x$, $y$ et $z$ (mis à part qu'ils sont positifs) puisque tout triplet de réels positifs $(x,y,z)$ donne exactement un triplet $(a,b,c)$ de réels vérifiant les inégalités triangulaires.
Cela est moins courant, mais il est aussi possible d'utiliser cette transformation même lorsque $a$, $b$ et $c$ sont des réels positifs quelconques. En effet, on peut alors séparer le problème en deux cas : l'un où l'une des $3$ inégalités triangulaires n'est pas vérifiée (ce qui peut permettre de progresser dans le problème) et l'autre où on peut utiliser la transformation de Ravi.
La difficulté dans ces cas là est de penser à l'utiliser. L'astuce c'est de repérer les expressions $b+c-a, a+b-c, c+a-b$. En effet la positivité de ces expressions est équivalente au fait que $a,b,c$ sont les côtés d'un triangle donc voir ces expressions apparaitre est un signe qu'une transformation de Ravi peut simplifier les choses.
$$S = \sqrt{p(p-a)(p-b)(p-c)}$$ où $p = \frac{a+b+c}{2}$ est le demi périmètre du triangle. Après la transformation de Ravi, cette formule devient
$$S = \sqrt{(x+y+z)xyz}.$$
Celle-ci peut en fait être appliquée lorsque l'on est en présence de trois variables $a$, $b$ et $c$ positives dont on sait qu'elles correspondent aux longueurs des trois côtés d'un même triangle, c'est-à-dire qu'elles vérifient les inégalités
$$\begin{align}
a + b & \geq c,\\[1mm]
b + c & \geq a,\\[1mm]
c + a & \geq b.
\end{align}$$ En pratique, cette condition est généralement énoncée telle quelle dans l'énoncé du problème : celui-ci commence par exemple par "Montrer que si $a$, $b$ et $c$ sont les longueurs des côtés d'un triangle, alors ils vérifient l'inégalité suivante".
La transformation de Ravi consiste alors à remplacer $a$, $b$ et $c$ par $x$, $y$ et $z$ (positifs) en effectuant le changement de variable
$$\left\{\begin{align}
a & = y+z \\[1mm]
b &= z + x \\[1mm]
c &= x + y
\end{align}\right.$$ ce qui revient en fait à poser
$$\left\{\begin{align}
x & = \frac{b + c - a}{2} \\[2mm]
y & = \frac{c + a - b}{2} \\[2mm]
z & = \frac{a + b - c}{2}
\end{align}\right.$$
Il existe une façon géométrique de visualiser ce changement de variables. En effet, si on dessine le triangle dont les longueurs des côtés sont $a$, $b$ et $c$, alors les valeurs de $x$, $y$ et $z$ peuvent être trouvées en traçant le cercle inscrit au triangle et évaluant les distances des points de tangence aux différents sommets, comme illustré sur la figure suivante.

Sur cette figure, on a $a = |BC|$, $b = |AC|$ et $c = |AB|$. De plus, on a les égalités de longueurs $|AQ| = |AR| = x$, $|BP| = |BR| = y$ et $|CP| = |CQ| = z$ car les triangles $AQI$ et $ARI$ sont isométriques, tout comme les triangles $BPI$ et $BRI$ et les triangles $CPI$ et $CQI$.
Cette transformation est d'une grande utilité lorsque les variables $a$, $b$ et $c$ sont supposées être les longueurs d'un triangle. En effet, elle permet de passer à une inégalité en $a$, $b$ et $c$ sous cette contrainte (qu'il ne semble a priori pas évident d'utiliser) à une inégalité équivalente en $x$, $y$ et $z$ sans contrainte. En effet, il n'y a plus aucune contrainte sur $x$, $y$ et $z$ (mis à part qu'ils sont positifs) puisque tout triplet de réels positifs $(x,y,z)$ donne exactement un triplet $(a,b,c)$ de réels vérifiant les inégalités triangulaires.
Cela est moins courant, mais il est aussi possible d'utiliser cette transformation même lorsque $a$, $b$ et $c$ sont des réels positifs quelconques. En effet, on peut alors séparer le problème en deux cas : l'un où l'une des $3$ inégalités triangulaires n'est pas vérifiée (ce qui peut permettre de progresser dans le problème) et l'autre où on peut utiliser la transformation de Ravi.
La difficulté dans ces cas là est de penser à l'utiliser. L'astuce c'est de repérer les expressions $b+c-a, a+b-c, c+a-b$. En effet la positivité de ces expressions est équivalente au fait que $a,b,c$ sont les côtés d'un triangle donc voir ces expressions apparaitre est un signe qu'une transformation de Ravi peut simplifier les choses.
Formule de Héron
La transformation de Ravi se combine bien avec la formule de Héron, expliquée en géométrie. Celle-ci stipule que l'aire d'un triangle de côtés $a$, $b$ et $c$ vaut$$S = \sqrt{p(p-a)(p-b)(p-c)}$$ où $p = \frac{a+b+c}{2}$ est le demi périmètre du triangle. Après la transformation de Ravi, cette formule devient
$$S = \sqrt{(x+y+z)xyz}.$$