Théorie > Géométrie > Quadrilatères cycliques
Prérequis
Résumé
La notion de quadrilatère cyclique est fondamentale en géométrie. La découverte d'un tel quadrilatère dans la figure associée à un problème est souvent un grand pas en avant vers sa résolution. Nous expliquons dans ce chapitre comment repérer un quadrilatère cyclique et comment utiliser par la suite cette information.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Premières propriétés
Un quadrilatère cyclique, parfois aussi appelé quadrilatère inscriptible, est un quadrilatère pouvant être inscrit dans un cercle. Cette nouvelle notion peut a priori sembler peu utile, mais c'est pourtant tout le contraire. Nous verrons dans la section suivante comment elle peut servir dans la résolution d'un problème. Nous exhibons d'abord quelques propriétés fondamentales des quadrilatères cycliques.
Cette propriété est triviale puisque, le quadrilatère $ABCD$ étant inscriptible, les deux angles cités sont des angles inscrits interceptant l'arc $AD$. En fait, nous verrons que la réciproque est également vraie, ce qui est moins évident.
Là aussi, nous allons voir que la réciproque est également vraie.
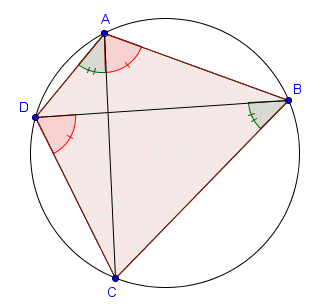
Propriété 1
Soit $ABCD$ un quadrilatère cyclique. On a $\widehat{ABD} = \widehat{ACD}$.
Cette propriété est triviale puisque, le quadrilatère $ABCD$ étant inscriptible, les deux angles cités sont des angles inscrits interceptant l'arc $AD$. En fait, nous verrons que la réciproque est également vraie, ce qui est moins évident.
Propriété 2
Les angles opposés d'un quadrilatère cyclique sont supplémentaires. Autrement dit, si $ABCD$ est cyclique, alors $\widehat{DAB}+\widehat{BCD} = 180^\circ$.

Démonstration
En considérant les angles du triangle $BCD$, on a
$$\widehat{BCD} = 180^\circ - \widehat{DBC} - \widehat{BDC}$$ Or, on a $\widehat{DBC} = \widehat{DAC}$ et $\widehat{BDC} = \widehat{BAC}$ (égalités d'angles inscrits), d'où
$$\widehat{BCD} = 180^\circ - \widehat{DAC} - \widehat{BAC} = 180^\circ - \widehat{DAB}$$ comme voulu.
$$\widehat{BCD} = 180^\circ - \widehat{DBC} - \widehat{BDC}$$ Or, on a $\widehat{DBC} = \widehat{DAC}$ et $\widehat{BDC} = \widehat{BAC}$ (égalités d'angles inscrits), d'où
$$\widehat{BCD} = 180^\circ - \widehat{DAC} - \widehat{BAC} = 180^\circ - \widehat{DAB}$$ comme voulu.
Là aussi, nous allons voir que la réciproque est également vraie.
2. Propriétés réciproques
Les deux petites propriétés énoncées dans la section précédente peuvent paraître bien anodines, puisqu'il s'agit juste d'égalités d'angles inscrits. En fait, ce sont surtout leurs réciproques qui sont intéressantes.
Exactement de la même manière, on peut montrer que dans un quadrilatère non cyclique, les angles opposés ne sont jamais supplémentaires.
Par exemple, si l'on constate (après une chasse aux angles) une situation du type $\widehat{ABD} = \widehat{ACD}$ (avec $B$ et $C$ du même côté de $AD$), alors les méthodes simples que nous avions présentées pour chasser les angles ne permettent pas de progresser davantage. Maintenant que nous connaissons les quadrilatères cycliques, on remarque qu'il est en fait possible de tirer énormément d'informations d'une telle égalité ! En effet, elle signifie que $ABCD$ est cyclique, ce qui nous permet directement de déduire que $\widehat{BCA} = \widehat{BDA}$, $\widehat{CDB} = \widehat{CAB}$, $\widehat{DAC} = \widehat{DBC}$, $\widehat{BAD}+\widehat{BCD} = 180^\circ$ et $\widehat{ABC} + \widehat{ADC} = 180^\circ$. On peut donc, à partir d'une simple égalité d'angles, en déduire $5$ autres ! En pratique, toutes ne sont bien sûr pas utiles, mais il est rare que la découverte d'un quadrilatère cyclique ne soit pas le début d'une avancée majeure dans la résolution d'un problème.
Propriété réciproque 1
Soit $ABCD$ un quadrilatère (non croisé). Si $\widehat{ABD} = \widehat{ACD}$, alors $ABCD$ est cyclique.
Démonstration
La façon la plus intuitive de démontrer ce résultat est de montrer sa contraposée, c'est-à-dire que l'on n'a pas l'égalité d'angles dans un quadrilatère non cyclique.
Considérons dès lors $ABCD$ un quadrilatère non cyclique et montrons que $\widehat{ABD} \neq \widehat{ACD}$. Le cercle $\Gamma$ circonscrit au triangle $ABD$ ne passe donc pas par $C$. On note alors $C'$ l'intersection de $AC$ avec $\Gamma$, et on a $C' \neq C$. Or, le quadrilatère $ABC'D$ est cyclique et nous savons donc qu'on a $\widehat{ABD} = \widehat{AC'D}$. Mais comme $C$ est du même côté de $AD$ que $C'$ (car le quadrilatère n'est pas croisé), on a forcément $\widehat{ACD} \neq \widehat{AC'D}$ et donc $\widehat{ACD} \neq \widehat{ABD}$.
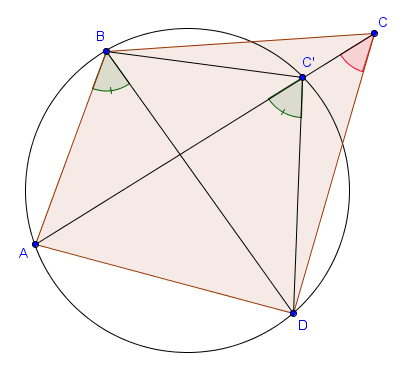
Considérons dès lors $ABCD$ un quadrilatère non cyclique et montrons que $\widehat{ABD} \neq \widehat{ACD}$. Le cercle $\Gamma$ circonscrit au triangle $ABD$ ne passe donc pas par $C$. On note alors $C'$ l'intersection de $AC$ avec $\Gamma$, et on a $C' \neq C$. Or, le quadrilatère $ABC'D$ est cyclique et nous savons donc qu'on a $\widehat{ABD} = \widehat{AC'D}$. Mais comme $C$ est du même côté de $AD$ que $C'$ (car le quadrilatère n'est pas croisé), on a forcément $\widehat{ACD} \neq \widehat{AC'D}$ et donc $\widehat{ACD} \neq \widehat{ABD}$.

Exactement de la même manière, on peut montrer que dans un quadrilatère non cyclique, les angles opposés ne sont jamais supplémentaires.
Propriété réciproque 2
Soit $ABCD$ un quadrilatère (non croisé). Si $\widehat{DAB}+\widehat{BCD}=180^\circ$, alors $ABCD$ est cyclique.
Remarque
Dans les deux propositions précédentes, l'hypothèse comme quoi le quadrilatère doit être non croisé peut être supprimée en utilisant des angles orientés. En effet, l'hypothèse $\widehat{ABD} = \widehat{ACD}$ où les angles sont supposés orientés implique d'elle-même que le quadrilatère est non croisé (car ces deux angles n'ont pas le même signe lorsque $ABCD$ est croisé).
Exemple d'utilisation
Ces résultats peuvent être d'une grande aide dans la résolution de problèmes, et notamment dans une chasse aux angles. En fait, on cherche souvent à trouver un quadrilatère cyclique (alors qu'aucun cercle ne laisse le présager). Pour cela, il suffit de trouver dans la figure qui nous intéresse des angles comme dans l'une des deux propriétés précédentes.Par exemple, si l'on constate (après une chasse aux angles) une situation du type $\widehat{ABD} = \widehat{ACD}$ (avec $B$ et $C$ du même côté de $AD$), alors les méthodes simples que nous avions présentées pour chasser les angles ne permettent pas de progresser davantage. Maintenant que nous connaissons les quadrilatères cycliques, on remarque qu'il est en fait possible de tirer énormément d'informations d'une telle égalité ! En effet, elle signifie que $ABCD$ est cyclique, ce qui nous permet directement de déduire que $\widehat{BCA} = \widehat{BDA}$, $\widehat{CDB} = \widehat{CAB}$, $\widehat{DAC} = \widehat{DBC}$, $\widehat{BAD}+\widehat{BCD} = 180^\circ$ et $\widehat{ABC} + \widehat{ADC} = 180^\circ$. On peut donc, à partir d'une simple égalité d'angles, en déduire $5$ autres ! En pratique, toutes ne sont bien sûr pas utiles, mais il est rare que la découverte d'un quadrilatère cyclique ne soit pas le début d'une avancée majeure dans la résolution d'un problème.
3. Théorème de Ptolémée
Nous avons vu comment caractériser les quadrilatères cycliques par des relations entre différents angles. Le théorème de Ptolémée permet de donner une condition nécessaire et suffisante sur les longueurs des côtés et des diagonales d'un quadrilatère pour que celui-ci soit cyclique.
Nous ne donnons pas la démonstration du sens $\Leftarrow$ maintenant, elle sera donnée dans un prochain chapitre.
Théorème de Ptolémée
Un quadrilatère (non croisé) $ABCD$ est cyclique si et seulement si
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
$$|AC|\cdot |BD| = |AB| \cdot |CD| + |BC| \cdot |AD|,$$ c'est-à-dire si le produit des longueurs de ses diagonales est égal à la somme des produits des longueurs des côtés opposés.
Nous ne donnons pas la démonstration du sens $\Leftarrow$ maintenant, elle sera donnée dans un prochain chapitre.
Démonstration du sens $\Rightarrow$
Considérons $ABCD$ un quadrilatère cyclique non-croisé. On note $K$ le point de $[AC]$ tel que $\widehat{ABK} = \widehat{DBC}$.
On a par angles inscrits que $\widehat{CAB} = \widehat{CDB}$, et les triangles $BKA$ et $BCD$ sont dès lors semblables.
Aussi, on a $\widehat{ACB} = \widehat{ADB}$, et puisque $\widehat{KBC} = \widehat{ABD}$ (au vu de notre choix de $K$), les triangles $CBK$ et $DBA$ sont à leur tour semblables.
On déduit de ces deux similitudes que
$$\frac{|KA|}{|BA|} = \frac{|CD|}{|BD|} \ \text{ et } \ \frac{|CK|}{|BC|} = \frac{|DA|}{|BD|},$$ ce qui se réécrit
$$|KA|\cdot|BD| = |CD|\cdot |BA| \ \text{ et } \ |CK| \cdot |BD| = |DA| \cdot |BC|.$$ Il ne reste alors plus qu'à sommer ces deux égalités pour obtenir, comme $|KA| + |CK| = |AC|$ :
$$|AC| \cdot |BD| = |CD| \cdot |BA| + |DA| \cdot |BC|.$$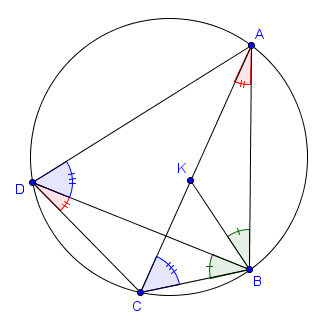
On a par angles inscrits que $\widehat{CAB} = \widehat{CDB}$, et les triangles $BKA$ et $BCD$ sont dès lors semblables.
Aussi, on a $\widehat{ACB} = \widehat{ADB}$, et puisque $\widehat{KBC} = \widehat{ABD}$ (au vu de notre choix de $K$), les triangles $CBK$ et $DBA$ sont à leur tour semblables.
On déduit de ces deux similitudes que
$$\frac{|KA|}{|BA|} = \frac{|CD|}{|BD|} \ \text{ et } \ \frac{|CK|}{|BC|} = \frac{|DA|}{|BD|},$$ ce qui se réécrit
$$|KA|\cdot|BD| = |CD|\cdot |BA| \ \text{ et } \ |CK| \cdot |BD| = |DA| \cdot |BC|.$$ Il ne reste alors plus qu'à sommer ces deux égalités pour obtenir, comme $|KA| + |CK| = |AC|$ :
$$|AC| \cdot |BD| = |CD| \cdot |BA| + |DA| \cdot |BC|.$$
