Théorie > Géométrie > Triangles
Aire d'un triangle
La façon la plus courante de calculer l'aire d'un triangle est d'utiliser la formule $\displaystyle \frac{\text{base} \times \text{hauteur}}{2}$. Malheureusement, cette formule s'applique rarement à un problème de géométrie, puisqu'il est rare qu'une hauteur du triangle auquel on s'intéresse soit déjà tracée. Il existe cependant d'autres formules pour calculer l'aire d'un triangle, la plus répandue étant certainement la suivante.
On peut aussi combiner cette formule avec la loi des sinus qui nous dit que $\displaystyle \frac{c}{\sin C} = 2R$, pour obtenir directement :
La formule de Héron, quant à elle, permet de calculer l'aire d'un triangle en connaissant uniquement la longueur de ses trois côtés !
Enfin, il existe encore une quatrième formule, cette fois contenant le rayon du cercle inscrit au triangle.
Formule (aire d'un triangle)
Soit $ABC$ un triangle de côtés $a = |BC|$, $b = |AC|$ et $c = |AB|$. L'aire de $ABC$ est donnée par
$$S = \frac{a\cdot b \cdot \sin C}{2}.$$
$$S = \frac{a\cdot b \cdot \sin C}{2}.$$
Démonstration
Si $P$ désigne le pied de la hauteur de $ABC$ relative à $A$, alors le triangle $APC$ est rectangle et on a $|AP| = |AC| \cdot \sin{\widehat{ACP}}$. Dès lors, on a
$$S = \frac{1}{2}\cdot |BC| \cdot |AP| = \frac{1}{2} \cdot |BC| \cdot |AC| \cdot \sin\widehat{ACB}.$$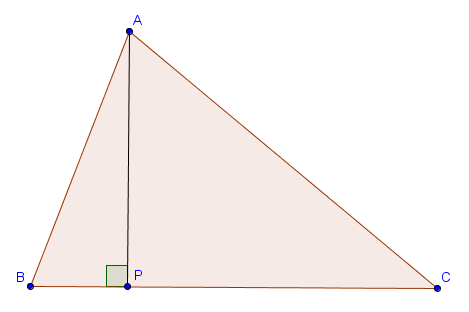
$$S = \frac{1}{2}\cdot |BC| \cdot |AP| = \frac{1}{2} \cdot |BC| \cdot |AC| \cdot \sin\widehat{ACB}.$$

On peut aussi combiner cette formule avec la loi des sinus qui nous dit que $\displaystyle \frac{c}{\sin C} = 2R$, pour obtenir directement :
Formule (aire d'un triangle)
Soit $ABC$ un triangle, $a$, $b$ et $c$ les longueurs de ses côtés, et $R$ le rayon de son cercle circonscrit. L'aire de $ABC$ est donnée par
$$S = \frac{abc}{4R}.$$
$$S = \frac{abc}{4R}.$$
La formule de Héron, quant à elle, permet de calculer l'aire d'un triangle en connaissant uniquement la longueur de ses trois côtés !
Formule de Héron (aire d'un triangle)
Soit $ABC$ un triangle et $a$, $b$ et $c$ les longueurs de ses côtés. Si $p$ désigne le demi-périmètre de $ABC$, c'est-à-dire si $\displaystyle p = \frac{a+b+c}{2}$, alors l'aire de $ABC$ vaut
$$S = \sqrt{p(p-a)(p-b)(p-c)}.$$
$$S = \sqrt{p(p-a)(p-b)(p-c)}.$$
Démonstration
Par la première formule, on a $\displaystyle S = \frac{a\cdot b \cdot \sin C}{2}$. Il suffit alors d'utiliser la loi des cosinus nous apprenant que $\displaystyle \cos C = \frac{a^2+b^2-c^2}{2ab}$ :
$$\begin{align}
S &= \frac{1}{2}\cdot a \cdot b \cdot \sin C \\
&= \frac{1}{2} \cdot a \cdot b \cdot \sqrt{1 - \cos^2 C}\\
& = \frac{1}{2} \cdot a \cdot b \cdot \sqrt{(1-\cos C) (1+\cos C)}\\
&= \frac{1}{2} \cdot a \cdot b \cdot \sqrt{\left(1 - \frac{a^2+b^2-c^2}{2ab} \right)\left(1 + \frac{a^2+b^2-c^2}{2ab} \right)}\\
&= \frac{1}{4} \cdot \sqrt{\left(2ab-a^2-b^2+c^2\right)\left(2ab+a^2+b^2-c^2\right)}\\
&= \frac{1}{4} \cdot \sqrt{\left(c^2-(a-b)^2\right)\left((a+b)^2-c^2\right)}\\
&= \frac{1}{4} \cdot \sqrt{(c+a-b)(c-a+b)(a+b+c)(a+b-c)}\\
&= \sqrt{\left(\frac{a-b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)\left(\frac{a+b+c}{2}\right)\left(\frac{a+b-c}{2}\right)}\\
&= \sqrt{(p-b)(p-a)p(p-c)}.
\end{align}$$
$$\begin{align}
S &= \frac{1}{2}\cdot a \cdot b \cdot \sin C \\
&= \frac{1}{2} \cdot a \cdot b \cdot \sqrt{1 - \cos^2 C}\\
& = \frac{1}{2} \cdot a \cdot b \cdot \sqrt{(1-\cos C) (1+\cos C)}\\
&= \frac{1}{2} \cdot a \cdot b \cdot \sqrt{\left(1 - \frac{a^2+b^2-c^2}{2ab} \right)\left(1 + \frac{a^2+b^2-c^2}{2ab} \right)}\\
&= \frac{1}{4} \cdot \sqrt{\left(2ab-a^2-b^2+c^2\right)\left(2ab+a^2+b^2-c^2\right)}\\
&= \frac{1}{4} \cdot \sqrt{\left(c^2-(a-b)^2\right)\left((a+b)^2-c^2\right)}\\
&= \frac{1}{4} \cdot \sqrt{(c+a-b)(c-a+b)(a+b+c)(a+b-c)}\\
&= \sqrt{\left(\frac{a-b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)\left(\frac{a+b+c}{2}\right)\left(\frac{a+b-c}{2}\right)}\\
&= \sqrt{(p-b)(p-a)p(p-c)}.
\end{align}$$
Enfin, il existe encore une quatrième formule, cette fois contenant le rayon du cercle inscrit au triangle.
Formule (aire d'un triangle)
Soit $ABC$ un triangle, $r$ le rayon de son cercle inscrit et $p$ son demi-périmètre. L'aire de $ABC$ vaut
$$S = pr.$$
$$S = pr.$$
Démonstration
Notons $I$ le centre du cercle inscrit au triangle. L'aire de $ABC$ est égale à la somme des aires des triangles $ABI$, $BCI$ et $CAI$, et ceux-ci ont chacun une hauteur égale à $r$. On a donc
$$S(ABC) = S(ABI) + S(BCI) + S(CAI) = \frac{|AB|\cdot r}{2} + \frac{|BC| \cdot r}{2} + \frac{|CA| \cdot r}{2} = pr.$$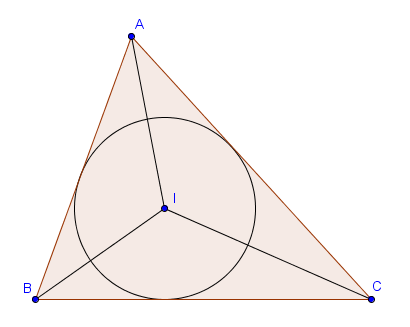
$$S(ABC) = S(ABI) + S(BCI) + S(CAI) = \frac{|AB|\cdot r}{2} + \frac{|BC| \cdot r}{2} + \frac{|CA| \cdot r}{2} = pr.$$
