Théorie > Géométrie > Rapports de section
Théorème de Ménélaüs
Le théorème de Ménélaüs est très similaire au théorème de Céva. Il donne cette fois une condition nécessaire et suffisante pour que trois points situés sur les côtés d'un triangle (ou sur leur prolongement) soient alignés.
Théorème de Ménélaüs
Soit $ABC$ un triangle et $D \in BC$, $E \in AC$, $F \in AB$ des points distincts des sommets. Les points $D$, $E$ et $F$ sont alignés si et seulement si
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = 1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
$$r_{AB}(F) \cdot r_{BC}(D) \cdot r_{CA}(E) = 1$$ ou, autrement dit, si
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Démonstration
Comme pour Ceva, on commence par le sens $\Rightarrow$. Notons $X$ l'intersection de $DF$ avec la parallèle à $BC$ passant par $A$, comme sur la figure ci-dessous.
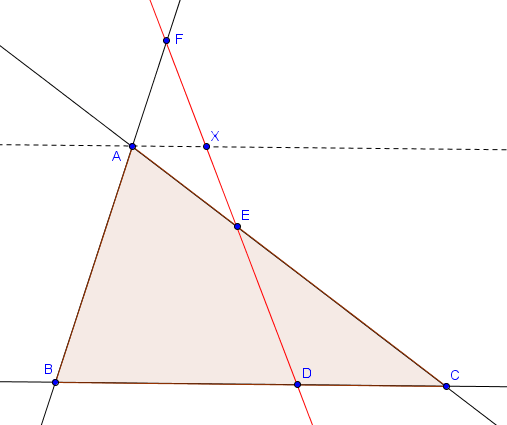
Par Thalès dans les triangles $BDF$ et $CDE$, on a les deux relations suivantes :
$$\frac{\overline{DB}}{\overline{XA}} = \frac{\overline{FB}}{\overline{FA}} \quad \text{ et } \quad \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{EA}}{\overline{EC}}.$$ On a donc
$$\frac{\overline{DB}}{\overline{DC}} = \frac{\overline{DB}}{\overline{XA}} \cdot \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{EA}}{\overline{EC}},$$ ce qui est équivalent à
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Passons au sens $\Leftarrow$. On suppose donc avoir
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$ Remarquons déjà que $EF$ ne peut pas être parallèle à $BC$. En effet, si tel était le cas, par Thalès on aurait
$$\frac{\overline{EA}}{\overline{EC}} = \frac{\overline{FA}}{\overline{FB}},$$ d'où $\displaystyle \frac{\overline{DC}}{\overline{DB}} = 1$ mais cela est impossible car un rapport de section ne vaut jamais $1$. On peut donc noter $D'$ l'intersection de $EF$ avec $BC$, et on montre comme dans la démonstration du théorème de Ceva que l'on a forcément $D = D'$.

Par Thalès dans les triangles $BDF$ et $CDE$, on a les deux relations suivantes :
$$\frac{\overline{DB}}{\overline{XA}} = \frac{\overline{FB}}{\overline{FA}} \quad \text{ et } \quad \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{EA}}{\overline{EC}}.$$ On a donc
$$\frac{\overline{DB}}{\overline{DC}} = \frac{\overline{DB}}{\overline{XA}} \cdot \frac{\overline{XA}}{\overline{DC}} = \frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{EA}}{\overline{EC}},$$ ce qui est équivalent à
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$
Passons au sens $\Leftarrow$. On suppose donc avoir
$$\frac{\overline{FB}}{\overline{FA}} \cdot \frac{\overline{DC}}{\overline{DB}} \cdot \frac{\overline{EA}}{\overline{EC}} = 1.$$ Remarquons déjà que $EF$ ne peut pas être parallèle à $BC$. En effet, si tel était le cas, par Thalès on aurait
$$\frac{\overline{EA}}{\overline{EC}} = \frac{\overline{FA}}{\overline{FB}},$$ d'où $\displaystyle \frac{\overline{DC}}{\overline{DB}} = 1$ mais cela est impossible car un rapport de section ne vaut jamais $1$. On peut donc noter $D'$ l'intersection de $EF$ avec $BC$, et on montre comme dans la démonstration du théorème de Ceva que l'on a forcément $D = D'$.