Théorie > Géométrie > Triangles (suite)
Prérequis
Résumé
Un certain nombre de résultats concernant les triangles ont été précédemment présentés. Nous donnons ici quelques résultats plus avancés dont les démonstrations font intervenir les quadrilatères cycliques et les puissances de points.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Relation d'Euler
La relation d'Euler est une égalité ayant lieu dans les triangles. Elle relie le rayon du cercle inscrit, le rayon du cercle circonscrit et la distance entre les centres des cercles inscrits et circonscrits.
Relation d'Euler
Soit $ABC$ un triangle, $R$ le rayon de son cercle circonscrit, $r$ le rayon de son cercle inscrit et $d$ la distance entre les centres des cercles inscrits et circonscrits. Alors
$$d^2 = R(R-2r).$$ En particulier, on a toujours $R \geq 2r$, avec égalité si et seulement si $ABC$ est équilatéral.
$$d^2 = R(R-2r).$$ En particulier, on a toujours $R \geq 2r$, avec égalité si et seulement si $ABC$ est équilatéral.
Démonstration
On note $I$ le centre du cercle inscrit et $O$ celui du cercle circonscrit. On note également $X$ l'intersection de $BI$ avec le cercle circonscrit et $X'$ le point diamétralement opposé à $X$ sur ce cercle. Enfin, on note $D$ le pied de la perpendiculaire à $BC$ passant par $I$.
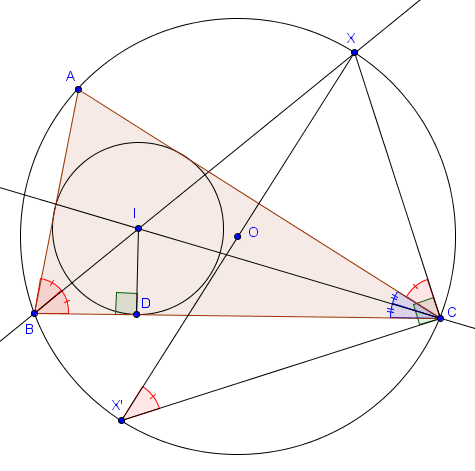
On commence par constater que les triangles $BDI$ et $X'CX$ sont semblables. En effet, ils sont tous les deux rectangles et on a $\widehat{IBD} = \widehat{XBC} = \widehat{XX'C}$ (angles inscrits). On a donc
$$\frac{|ID|}{|IB|} = \frac{|XC|}{|XX'|},$$ c'est-à-dire, puisque $|ID| = r$ et $XX' = 2R$ :
$$|XC| \cdot |IB| = 2Rr.$$ De plus, on a les égalités d'angles
$$\widehat{XIC} = 180^\circ - \widehat{BIC} = \widehat{IBC} + \widehat{ICB} = \frac{\widehat{ABC}+\widehat{ACB}}{2}$$ et
$$\widehat{ICX} = \widehat{ICA}+\widehat{ACX} = \widehat{ICA}+\widehat{ABX} = \frac{\widehat{ABC}+\widehat{ACB}}{2},$$ ce qui signifie que le triangle $IXC$ est isocèle avec $|XI| = |XC|$. La relation trouvée plus haut devient donc
$$|XI|\cdot |IB| = 2Rr.$$ Or, on reconnait en $|XI| \cdot |IB|$ la puissance (au signe près) du point $I$ par rapport au cercle circonscrit. Celle-ci étant, par définition, égale à $d^2-R^2$, on obtient la relation
$$d^2 - R^2 = -2Rr$$ qui est équivalente à la relation d'Euler.
Finalement, on a $0 \leq d^2 = R(R-2r)$ d'où $R \geq 2r$, et l'égalité a lieu si et seulement si $d = 0$, c'est-à-dire si $I = O$. C'est un simple exercice de vérifier que cela n'arrive que lorsque $ABC$ est équilatéral.

On commence par constater que les triangles $BDI$ et $X'CX$ sont semblables. En effet, ils sont tous les deux rectangles et on a $\widehat{IBD} = \widehat{XBC} = \widehat{XX'C}$ (angles inscrits). On a donc
$$\frac{|ID|}{|IB|} = \frac{|XC|}{|XX'|},$$ c'est-à-dire, puisque $|ID| = r$ et $XX' = 2R$ :
$$|XC| \cdot |IB| = 2Rr.$$ De plus, on a les égalités d'angles
$$\widehat{XIC} = 180^\circ - \widehat{BIC} = \widehat{IBC} + \widehat{ICB} = \frac{\widehat{ABC}+\widehat{ACB}}{2}$$ et
$$\widehat{ICX} = \widehat{ICA}+\widehat{ACX} = \widehat{ICA}+\widehat{ABX} = \frac{\widehat{ABC}+\widehat{ACB}}{2},$$ ce qui signifie que le triangle $IXC$ est isocèle avec $|XI| = |XC|$. La relation trouvée plus haut devient donc
$$|XI|\cdot |IB| = 2Rr.$$ Or, on reconnait en $|XI| \cdot |IB|$ la puissance (au signe près) du point $I$ par rapport au cercle circonscrit. Celle-ci étant, par définition, égale à $d^2-R^2$, on obtient la relation
$$d^2 - R^2 = -2Rr$$ qui est équivalente à la relation d'Euler.
Finalement, on a $0 \leq d^2 = R(R-2r)$ d'où $R \geq 2r$, et l'égalité a lieu si et seulement si $d = 0$, c'est-à-dire si $I = O$. C'est un simple exercice de vérifier que cela n'arrive que lorsque $ABC$ est équilatéral.
2. Symédianes
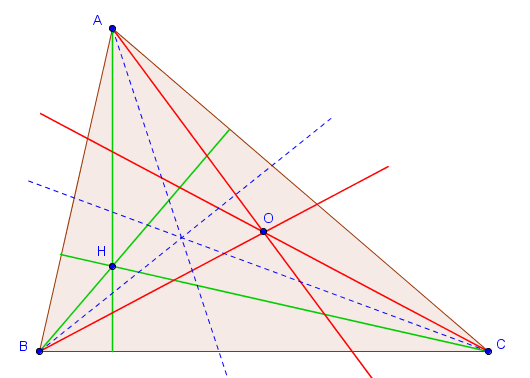
Les symédianes d'un triangle sont définies comme étant les droites symétriques des médianes par rapport aux bissectrices. Sur la figure suivante, les médianes sont représentées en vert, les bissectrices en bleu (pointillé) et les symédianes en rouge.
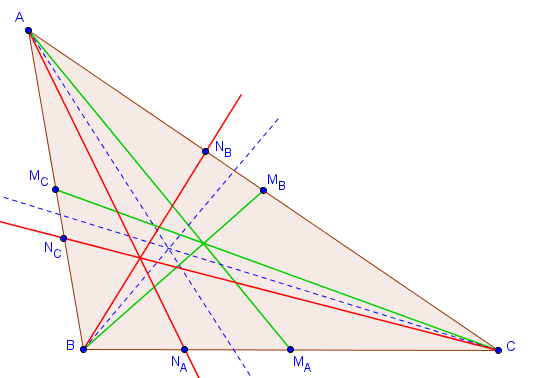
Comme on peut le constater sur cette figure, les trois symédianes d'un triangle semblent être concourantes. C'est effectivement toujours le cas :
Le point de Lemoine possède différentes propriétés. Par exemple, il s'agit du point dont la somme des carrés des distances aux côtés du triangle est minimale.
Le lien avec les symédianes est que la symédiane de $ABC$ provenant de $A$ est exactement le lieu des milieux des segments $[B'C']$ où $B'C'$ est antiparallèle à $BC$ (avec $B' \in AB$ et $C' \in AC$ comme défini ci-dessus). C'est un simple corollaire de la définition de symédiane et du fait que la médiane coupe $[BC]$ en son milieu.
Cela étant, on ne définit généralement pas les "syhauteurs", et ce pour une bonne raison : elles correspondent à des droites particulières du triangle que l'on connait déjà ! Il suffit d'une petite chasse aux angles pour s'en rendre compte.
On note $H$ l'orthocentre du triangle et $O$ le point d'intersection des "syhauteurs". On a
$$\widehat{OAC} = \widehat{HAB} = 90^\circ - \widehat{ABC},$$ $$\widehat{OCA} = \widehat{HCB} = 90^\circ - \widehat{ABC}.$$ Donc $\widehat{OAC} = \widehat{OCA}$, ce qui signifie que $|OA| = |OC|$. De la même façon, on trouve bien sûr $|OA| = |OB|$ et $|OB| = |OC|$. L'intersection des "syhauteurs" n'est donc rien d'autre que le centre du cercle circonscrit au triangle $ABC$ (et on comprend pourquoi nous avons choisi la notation $O$). Les "syhauteurs" ne sont donc que les droites prolongeant les rayons $OA$, $OB$ et $OC$ du cercle circonscrit à $ABC$.
C'est pour cette raison qu'on ne définit pas les "syhauteurs", mais il est tout de même bon de se souvenir que, dans un triangle $ABC$ d'orthocentre $H$ et de centre du cercle circonscrit $O$, les droites $OA$ et $HA$ sont symétriques par rapport à la bissectrice de $A$ (et de même pour $B$ et $C$).

Comme on peut le constater sur cette figure, les trois symédianes d'un triangle semblent être concourantes. C'est effectivement toujours le cas :
Propriété (définition du point de Lemoine)
Les trois symédianes d'un triangle se rencontrent en un point : le point de Lemoine du triangle.
Démonstration
Il suffit en fait d'utiliser la version trigonométrique du théorème de Ceva. Selon ce théorème, les trois symédianes sont concourantes si et seulement si
$$\frac{\sin \widehat{N_CCB}}{\sin \widehat{N_CCA}} \cdot \frac{\sin\widehat{N_AAC}}{\sin \widehat{N_AAB}} \cdot \frac{\sin \widehat{N_BBA}}{\sin \widehat{N_BBC}} = 1.$$ Or, vu que les symédianes sont les droites symétriques aux médianes par rapport aux bissectrices, on a $\widehat{N_CCB} = \widehat{M_CCA}$, $\widehat{N_CCA} = \widehat{M_CCB}$ et de même pour les quatre autres angles. La dernière relation s'écrit donc
$$\frac{\sin \widehat{M_CCA}}{\sin \widehat{M_CCB}} \cdot \frac{\sin\widehat{M_AAB}}{\sin \widehat{M_AAC}} \cdot \frac{\sin \widehat{M_BBC}}{\sin \widehat{M_BBA}} = 1.$$ Mais cette relation est, quitte à inverser le membre de gauche, exactement la version trigonométrique du théorème de Ceva pour les trois médianes du triangle $ABC$. Comme on sait déjà que les médianes sont concourantes, cette relation est bien vérifiée et les symédianes sont à leur tour concourantes.
$$\frac{\sin \widehat{N_CCB}}{\sin \widehat{N_CCA}} \cdot \frac{\sin\widehat{N_AAC}}{\sin \widehat{N_AAB}} \cdot \frac{\sin \widehat{N_BBA}}{\sin \widehat{N_BBC}} = 1.$$ Or, vu que les symédianes sont les droites symétriques aux médianes par rapport aux bissectrices, on a $\widehat{N_CCB} = \widehat{M_CCA}$, $\widehat{N_CCA} = \widehat{M_CCB}$ et de même pour les quatre autres angles. La dernière relation s'écrit donc
$$\frac{\sin \widehat{M_CCA}}{\sin \widehat{M_CCB}} \cdot \frac{\sin\widehat{M_AAB}}{\sin \widehat{M_AAC}} \cdot \frac{\sin \widehat{M_BBC}}{\sin \widehat{M_BBA}} = 1.$$ Mais cette relation est, quitte à inverser le membre de gauche, exactement la version trigonométrique du théorème de Ceva pour les trois médianes du triangle $ABC$. Comme on sait déjà que les médianes sont concourantes, cette relation est bien vérifiée et les symédianes sont à leur tour concourantes.
Le point de Lemoine possède différentes propriétés. Par exemple, il s'agit du point dont la somme des carrés des distances aux côtés du triangle est minimale.
Symédianes et antiparallèles
Étant donné un triangle $ABC$, on dit qu'une antiparallèle à $BC$ est une droite dont l'intersection $B'$ avec $AB$ et l'intersection $C'$ avec $AC$ sont telles que $AB'C'$ est semblable à $ACB$ (les sommets dans cet ordre). Si on avait demandé qu'il soit semblable à $ABC$, alors on aurait simplement eu la définition de parallèle. Une telle antiparallèle est telle que le quadrilatère $BB'C'C$ est cyclique.Le lien avec les symédianes est que la symédiane de $ABC$ provenant de $A$ est exactement le lieu des milieux des segments $[B'C']$ où $B'C'$ est antiparallèle à $BC$ (avec $B' \in AB$ et $C' \in AC$ comme défini ci-dessus). C'est un simple corollaire de la définition de symédiane et du fait que la médiane coupe $[BC]$ en son milieu.

Quid des "syhauteurs" ?
Dans la démonstration du fait que les symédianes sont concourantes, nous avons uniquement utilisé que les médianes sont concourantes et que les symédianes sont les symétriques des médianes. On peut donc effectuer exactement la même démonstration dès que l'on est en présence de trois droites concourantes issues de $A$, $B$ et $C$ et que l'on considère leurs symétriques par rapport aux bissectrices. On peut notamment être tenté de définir les "syhauteurs" d'un triangle comme étant les droites symétriques des hauteurs par rapport aux bissectrices, et on aurait directement que les "syhauteurs" sont concourantes.Cela étant, on ne définit généralement pas les "syhauteurs", et ce pour une bonne raison : elles correspondent à des droites particulières du triangle que l'on connait déjà ! Il suffit d'une petite chasse aux angles pour s'en rendre compte.

On note $H$ l'orthocentre du triangle et $O$ le point d'intersection des "syhauteurs". On a
$$\widehat{OAC} = \widehat{HAB} = 90^\circ - \widehat{ABC},$$ $$\widehat{OCA} = \widehat{HCB} = 90^\circ - \widehat{ABC}.$$ Donc $\widehat{OAC} = \widehat{OCA}$, ce qui signifie que $|OA| = |OC|$. De la même façon, on trouve bien sûr $|OA| = |OB|$ et $|OB| = |OC|$. L'intersection des "syhauteurs" n'est donc rien d'autre que le centre du cercle circonscrit au triangle $ABC$ (et on comprend pourquoi nous avons choisi la notation $O$). Les "syhauteurs" ne sont donc que les droites prolongeant les rayons $OA$, $OB$ et $OC$ du cercle circonscrit à $ABC$.
C'est pour cette raison qu'on ne définit pas les "syhauteurs", mais il est tout de même bon de se souvenir que, dans un triangle $ABC$ d'orthocentre $H$ et de centre du cercle circonscrit $O$, les droites $OA$ et $HA$ sont symétriques par rapport à la bissectrice de $A$ (et de même pour $B$ et $C$).
3. Triangle podaire et droite de Simson
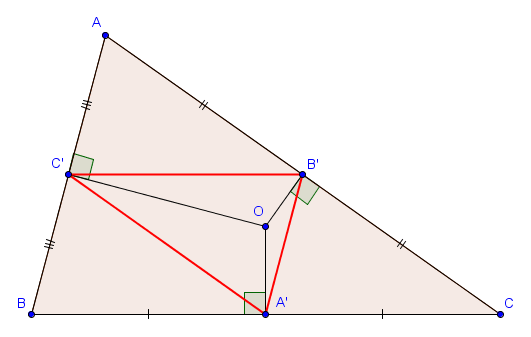
Étant donné un triangle $ABC$ et un point $P$ quelconque dans le plan, on appelle triangle podaire relatif à $P$ le triangle $A'B'C'$ dont les sommets $A'$, $B'$ et $C'$ sont les projections orthogonales de $P$ sur $BC$, $AC$ et $AB$, respectivement.
Sur la figure suivante, le point $P$ est à l'intérieur du triangle, mais il peut tout à fait se situer à l'extérieur.
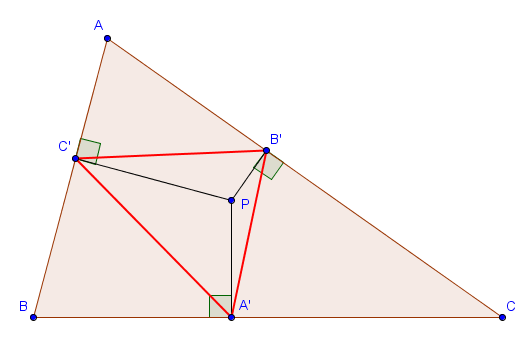
Les triangles podaires apparaîssent parfois dans des problèmes de géométrie. Une première remarque que l'on peut toujours faire est que, dans une telle situation, les quadrilatères $AB'PC'$, $BC'PA'$ et $CA'PB'$ sont toujours cycliques, de diamètres respectifs $[AP]$, $[BP]$ et $[CP]$. Cette information permet notamment de trouver les longueurs des côtés du triangle podaire $A'B'C'$ en fonction d'autres paramètres. En effet, par la loi des sinus dans le triangle $AB'C'$, on a par exemple
$$|B'C'| = |PA| \cdot \sin A$$ (où $|PA|$ prend le rôle de $2R$ dans la loi des sinus).
Observons à présent les propriétés des triangles podaires relatifs à certains points particuliers du triangle.
Sur la figure suivante, le point $P$ est à l'intérieur du triangle, mais il peut tout à fait se situer à l'extérieur.

Les triangles podaires apparaîssent parfois dans des problèmes de géométrie. Une première remarque que l'on peut toujours faire est que, dans une telle situation, les quadrilatères $AB'PC'$, $BC'PA'$ et $CA'PB'$ sont toujours cycliques, de diamètres respectifs $[AP]$, $[BP]$ et $[CP]$. Cette information permet notamment de trouver les longueurs des côtés du triangle podaire $A'B'C'$ en fonction d'autres paramètres. En effet, par la loi des sinus dans le triangle $AB'C'$, on a par exemple
$$|B'C'| = |PA| \cdot \sin A$$ (où $|PA|$ prend le rôle de $2R$ dans la loi des sinus).
Observons à présent les propriétés des triangles podaires relatifs à certains points particuliers du triangle.
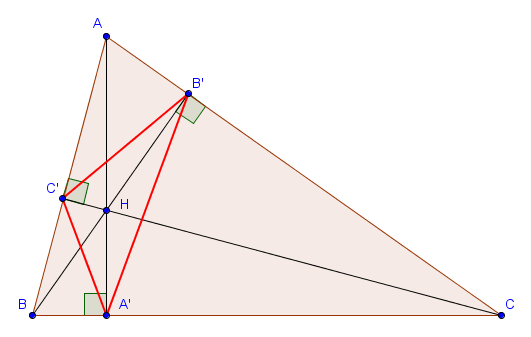
- Si $P = O$, le centre du cercle circonscrit à $ABC$, alors comme $O$ se situe sur les médiatrices des différents côtés, les points $A'$, $B'$ et $C'$ sont les milieux des côtés $[BC]$, $[AC]$ et $[AB]$, respectivement.
Dans ce cas, la situation est très claire. En effet, par Thalès, $B'C'$ est parallèle à $BC$, $A'C'$ est parallèle à $AC$ et $A'B'$ est parallèle à $AB$. Le triangle $A'B'C'$ est donc semblable à $ABC$ (avec un rapport $\frac{1}{2}$). De plus, le point $O$ n'est rien d'autre que l'orthocentre du triangle $A'B'C'$, puisque $A'O$ est perpendiculaire à $BC$ et donc également à $B'C'$. (et de même pour $B'O$ et $C'O$). En fait, on se rend compte que la construction que nous venons de faire est exactement la construction inverse de celle que nous avons faite pour prouver que les trois hauteurs d'un triangle sont concourantes. - Si $P = H$, l'orthocentre de $ABC$, alors les points $A'$, $B'$ et $C'$ sont les pieds des hauteurs issues de $A$, $B$ et $C$, respectivement. Le triangle $A'B'C'$ est également appelé dans ce cas le triangle orthique.
Afin que $H$ reste à l'intérieur de $ABC$, nous supposons dorénavant que le triangle $ABC$ est acutangle. On peut alors utiliser le fait que $AB'HC'$ et $CA'HB'$ sont cycliques pour trouver :
$$\widehat{HB'C'} = \widehat{HAC'} = 90^\circ - \widehat{ABC},$$ $$\widehat{HB'A'} = \widehat{HCA'} = 90^\circ - \widehat{ABC}.$$ Nous venons donc de montrer que $H$ est sur la bissectrice de l'angle $\widehat{A'B'C'}$. De la même manière, il est sur les deux autres bissectrices du triangle podaire et on en déduit que $H$ est en fait le centre du cercle inscrit à $A'B'C'$. (Attention : cela n'est vrai que si $ABC$ est acutangle.)
Droite de Simson
Nous parlons de triangle podaire, mais il n'est a priori pas impossible que, pour un certain choix de $P$, les points $A'$, $B'$ et $C'$ soient alignés ! Dans un tel cas, on ne parle plus réellement de triangle podaire, mais plutôt de droite de Simson associée à $P$. En fait, il existe une condition nécessaire et suffisante sur $P$ pour que le triangle podaire se transforme en droite de Simson :Théorème (droite de Simson)
Soit $ABC$ un triangle et $P$ un point quelconque du plan. Les projections $A'$, $B'$ et $C'$ du point $P$ sur les droites $BC$, $AC$ et $AB$ respectivement sont alignées si et seulement si $P$ appartient au cercle circonscrit au triangle $ABC$.
Démonstration
Nous donnons la démonstration en supposant que les différents points sont situés comme sur la figure suivante (c'est-à-dire tels que $B' \in [AC]$ et $A' \in [BC]$ mais $A \in [BC']$).
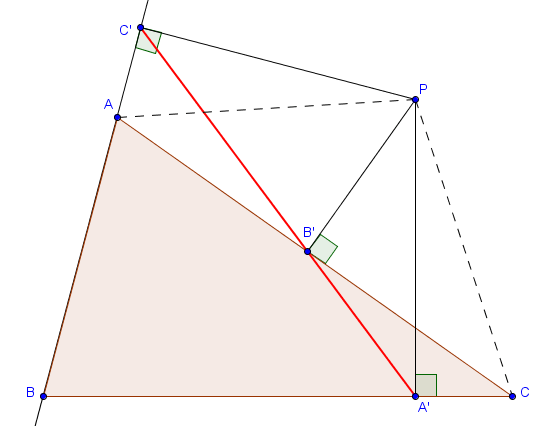
Les trois points $A'$, $B'$ et $C'$ sont alors alignés si et seulement si $\widehat{PB'A'} + \widehat{PB'C'} = 180^\circ$.
Or, le quadrilatère $PB'A'C$ étant cyclique, on a
$$\widehat{PB'A'} = 180^\circ - \widehat{PCA'} = 180^\circ - \widehat{PCB}.$$ De la même façon, $PB'AC'$ est cyclique et on en déduit
$$\widehat{PB'C'} = \widehat{PAC'} = 180^\circ - \widehat{PAB}.$$ Les trois points sont donc alignés si et seulement si $\widehat{PCB} + \widehat{PAB} = 180^\circ$, ce qui revient exactement à dire que $P$ se situe sur le cercle circonscrit à $ABC$.

Les trois points $A'$, $B'$ et $C'$ sont alors alignés si et seulement si $\widehat{PB'A'} + \widehat{PB'C'} = 180^\circ$.
Or, le quadrilatère $PB'A'C$ étant cyclique, on a
$$\widehat{PB'A'} = 180^\circ - \widehat{PCA'} = 180^\circ - \widehat{PCB}.$$ De la même façon, $PB'AC'$ est cyclique et on en déduit
$$\widehat{PB'C'} = \widehat{PAC'} = 180^\circ - \widehat{PAB}.$$ Les trois points sont donc alignés si et seulement si $\widehat{PCB} + \widehat{PAB} = 180^\circ$, ce qui revient exactement à dire que $P$ se situe sur le cercle circonscrit à $ABC$.
4. Triangle tangentiel
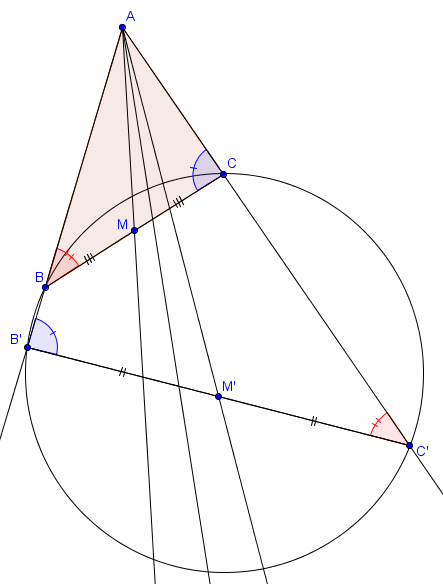
À un triangle $ABC$, on peut associer un autre triangle, dit triangle tangentiel. Pour le définir, il suffit de considérer $\Gamma$ le cercle circonscrit à $ABC$ et de tracer les tangentes à $\Gamma$ en $A$, $B$ et $C$. Celles-ci forment un triangle, et c'est celui-ci que l'on appelle triangle tangentiel.
Lien avec les symédianes
On peut retrouver, en construisant le triangle tangentiel, les symédianes d'un triangle.Proposition (triangle tangentiel et symédianes)
Soit $A'B'C'$ le triangle tangentiel associé à $ABC$ (de sorte que $A \in [B'C']$, $B \in [A'C']$ et $C \in [A'B']$). Les droites $AA'$, $BB'$ et $CC'$ sont les symédianes du triangle $ABC$.
Démonstration
Montrons que $AA'$ est la symédiane de $ABC$ partant de $A$. Pour ce faire, il suffit de prouver que $A'$ est le milieu d'une antiparallèle à $BC$. Traçons donc simplement l'antiparallèle à $BC$ passant par $A'$. On note $B''$ l'intersection de celle-ci avec $AB$ et $C''$ son intersection avec $AC$, et il faut prouver que $|B''A'| = |A'C''|$.
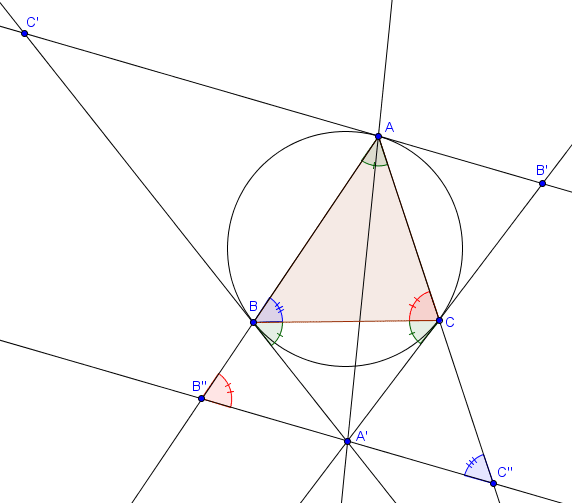
Par définition d'antiparallèle, on a $\widehat{AB''A'} = \widehat{ACB}$ et $\widehat{AC''A'} = \widehat{ABC}$. De plus, comme $\widehat{A'BC} = \widehat{BAC}$ (angles tangentiel et inscrit), on trouve
$$\widehat{B''BA'} = 180^\circ - \widehat{A'BC} - \widehat{CBA} = 180^\circ - \widehat{BAC} - \widehat{CBA} = \widehat{ACB} = \widehat{AB''A'}.$$ On en déduit que $BA'B''$ est isocèle, et de la même façon que $CA'C''$ est isocèle. On a donc
$$|A'B''| = |A'B| = |A'C| = |A'C''|,$$ comme voulu.

Par définition d'antiparallèle, on a $\widehat{AB''A'} = \widehat{ACB}$ et $\widehat{AC''A'} = \widehat{ABC}$. De plus, comme $\widehat{A'BC} = \widehat{BAC}$ (angles tangentiel et inscrit), on trouve
$$\widehat{B''BA'} = 180^\circ - \widehat{A'BC} - \widehat{CBA} = 180^\circ - \widehat{BAC} - \widehat{CBA} = \widehat{ACB} = \widehat{AB''A'}.$$ On en déduit que $BA'B''$ est isocèle, et de la même façon que $CA'C''$ est isocèle. On a donc
$$|A'B''| = |A'B| = |A'C| = |A'C''|,$$ comme voulu.
Lien avec le triangle orthique
On peut également remarquer que le triangle tangentiel est semblable au triangle orthique. En fait, on a plus précisément le résultat suivant.Proposition (triangles tangentiel et orthique)
Les côtés du triangle tangentiel sont parallèles aux côtés du triangle orthique.
Démonstration
Notons $H_A$, $H_B$ et $H_C$ les pieds des hauteurs de $ABC$. On doit montrer que $H_BH_C$ est parallèle à $B'C'$. Si $O$ désigne le centre du cercle circonscrit à $ABC$, on sait que $OA$ est perpendiculaire à $B'C'$. Il suffit donc de prouver que $OA$ est également perpendiculaire à $H_BH_C$. Il s'agit en fait d'une simple chasse aux angles. En effet, on a
$$\widehat{H_BH_CA} = \widehat{ACB}$$ car $BH_CH_BC$ est cyclique et
$$\widehat{H_CAO} = \frac{180^\circ-\widehat{AOB}}{2} = 90^\circ - \widehat{ACB},$$ d'où $\widehat{H_BH_CA} + \widehat{H_CAO} = 90^\circ$, ce qui suffit à prouver que $H_BH_C$ est perpendiculaire à $AO$.
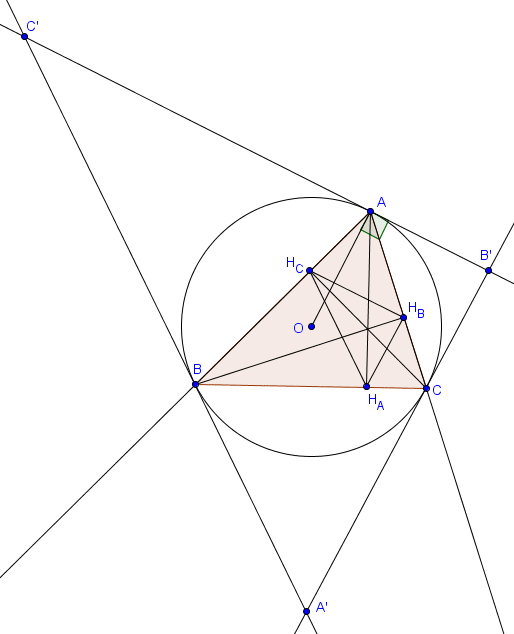
$$\widehat{H_BH_CA} = \widehat{ACB}$$ car $BH_CH_BC$ est cyclique et
$$\widehat{H_CAO} = \frac{180^\circ-\widehat{AOB}}{2} = 90^\circ - \widehat{ACB},$$ d'où $\widehat{H_BH_CA} + \widehat{H_CAO} = 90^\circ$, ce qui suffit à prouver que $H_BH_C$ est perpendiculaire à $AO$.