Théorie > Géométrie > Triangles (suite)
Symédianes
Les symédianes d'un triangle sont définies comme étant les droites symétriques des médianes par rapport aux bissectrices. Sur la figure suivante, les médianes sont représentées en vert, les bissectrices en bleu (pointillé) et les symédianes en rouge.
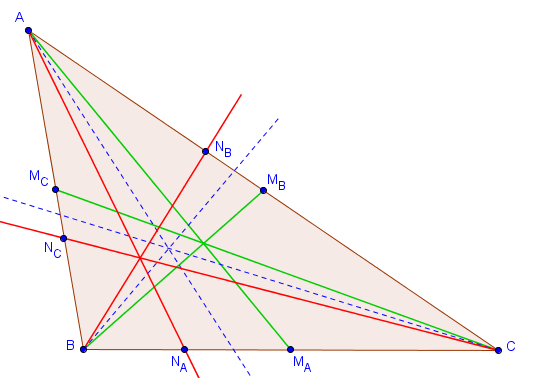
Comme on peut le constater sur cette figure, les trois symédianes d'un triangle semblent être concourantes. C'est effectivement toujours le cas :
Le point de Lemoine possède différentes propriétés. Par exemple, il s'agit du point dont la somme des carrés des distances aux côtés du triangle est minimale.
Le lien avec les symédianes est que la symédiane de $ABC$ provenant de $A$ est exactement le lieu des milieux des segments $[B'C']$ où $B'C'$ est antiparallèle à $BC$ (avec $B' \in AB$ et $C' \in AC$ comme défini ci-dessus). C'est un simple corollaire de la définition de symédiane et du fait que la médiane coupe $[BC]$ en son milieu.
Cela étant, on ne définit généralement pas les "syhauteurs", et ce pour une bonne raison : elles correspondent à des droites particulières du triangle que l'on connait déjà ! Il suffit d'une petite chasse aux angles pour s'en rendre compte.
On note $H$ l'orthocentre du triangle et $O$ le point d'intersection des "syhauteurs". On a
$$\widehat{OAC} = \widehat{HAB} = 90^\circ - \widehat{ABC},$$ $$\widehat{OCA} = \widehat{HCB} = 90^\circ - \widehat{ABC}.$$ Donc $\widehat{OAC} = \widehat{OCA}$, ce qui signifie que $|OA| = |OC|$. De la même façon, on trouve bien sûr $|OA| = |OB|$ et $|OB| = |OC|$. L'intersection des "syhauteurs" n'est donc rien d'autre que le centre du cercle circonscrit au triangle $ABC$ (et on comprend pourquoi nous avons choisi la notation $O$). Les "syhauteurs" ne sont donc que les droites prolongeant les rayons $OA$, $OB$ et $OC$ du cercle circonscrit à $ABC$.
C'est pour cette raison qu'on ne définit pas les "syhauteurs", mais il est tout de même bon de se souvenir que, dans un triangle $ABC$ d'orthocentre $H$ et de centre du cercle circonscrit $O$, les droites $OA$ et $HA$ sont symétriques par rapport à la bissectrice de $A$ (et de même pour $B$ et $C$).

Comme on peut le constater sur cette figure, les trois symédianes d'un triangle semblent être concourantes. C'est effectivement toujours le cas :
Propriété (définition du point de Lemoine)
Les trois symédianes d'un triangle se rencontrent en un point : le point de Lemoine du triangle.
Démonstration
Il suffit en fait d'utiliser la version trigonométrique du théorème de Ceva. Selon ce théorème, les trois symédianes sont concourantes si et seulement si
$$\frac{\sin \widehat{N_CCB}}{\sin \widehat{N_CCA}} \cdot \frac{\sin\widehat{N_AAC}}{\sin \widehat{N_AAB}} \cdot \frac{\sin \widehat{N_BBA}}{\sin \widehat{N_BBC}} = 1.$$ Or, vu que les symédianes sont les droites symétriques aux médianes par rapport aux bissectrices, on a $\widehat{N_CCB} = \widehat{M_CCA}$, $\widehat{N_CCA} = \widehat{M_CCB}$ et de même pour les quatre autres angles. La dernière relation s'écrit donc
$$\frac{\sin \widehat{M_CCA}}{\sin \widehat{M_CCB}} \cdot \frac{\sin\widehat{M_AAB}}{\sin \widehat{M_AAC}} \cdot \frac{\sin \widehat{M_BBC}}{\sin \widehat{M_BBA}} = 1.$$ Mais cette relation est, quitte à inverser le membre de gauche, exactement la version trigonométrique du théorème de Ceva pour les trois médianes du triangle $ABC$. Comme on sait déjà que les médianes sont concourantes, cette relation est bien vérifiée et les symédianes sont à leur tour concourantes.
$$\frac{\sin \widehat{N_CCB}}{\sin \widehat{N_CCA}} \cdot \frac{\sin\widehat{N_AAC}}{\sin \widehat{N_AAB}} \cdot \frac{\sin \widehat{N_BBA}}{\sin \widehat{N_BBC}} = 1.$$ Or, vu que les symédianes sont les droites symétriques aux médianes par rapport aux bissectrices, on a $\widehat{N_CCB} = \widehat{M_CCA}$, $\widehat{N_CCA} = \widehat{M_CCB}$ et de même pour les quatre autres angles. La dernière relation s'écrit donc
$$\frac{\sin \widehat{M_CCA}}{\sin \widehat{M_CCB}} \cdot \frac{\sin\widehat{M_AAB}}{\sin \widehat{M_AAC}} \cdot \frac{\sin \widehat{M_BBC}}{\sin \widehat{M_BBA}} = 1.$$ Mais cette relation est, quitte à inverser le membre de gauche, exactement la version trigonométrique du théorème de Ceva pour les trois médianes du triangle $ABC$. Comme on sait déjà que les médianes sont concourantes, cette relation est bien vérifiée et les symédianes sont à leur tour concourantes.
Le point de Lemoine possède différentes propriétés. Par exemple, il s'agit du point dont la somme des carrés des distances aux côtés du triangle est minimale.
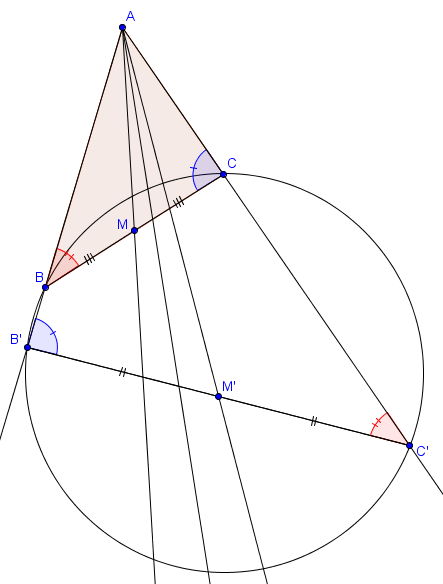
Symédianes et antiparallèles
Étant donné un triangle $ABC$, on dit qu'une antiparallèle à $BC$ est une droite dont l'intersection $B'$ avec $AB$ et l'intersection $C'$ avec $AC$ sont telles que $AB'C'$ est semblable à $ACB$ (les sommets dans cet ordre). Si on avait demandé qu'il soit semblable à $ABC$, alors on aurait simplement eu la définition de parallèle. Une telle antiparallèle est telle que le quadrilatère $BB'C'C$ est cyclique.Le lien avec les symédianes est que la symédiane de $ABC$ provenant de $A$ est exactement le lieu des milieux des segments $[B'C']$ où $B'C'$ est antiparallèle à $BC$ (avec $B' \in AB$ et $C' \in AC$ comme défini ci-dessus). C'est un simple corollaire de la définition de symédiane et du fait que la médiane coupe $[BC]$ en son milieu.

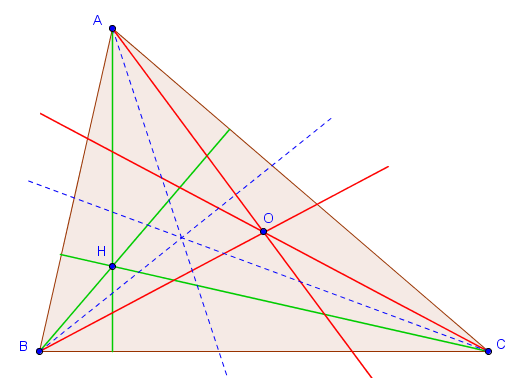
Quid des "syhauteurs" ?
Dans la démonstration du fait que les symédianes sont concourantes, nous avons uniquement utilisé que les médianes sont concourantes et que les symédianes sont les symétriques des médianes. On peut donc effectuer exactement la même démonstration dès que l'on est en présence de trois droites concourantes issues de $A$, $B$ et $C$ et que l'on considère leurs symétriques par rapport aux bissectrices. On peut notamment être tenté de définir les "syhauteurs" d'un triangle comme étant les droites symétriques des hauteurs par rapport aux bissectrices, et on aurait directement que les "syhauteurs" sont concourantes.Cela étant, on ne définit généralement pas les "syhauteurs", et ce pour une bonne raison : elles correspondent à des droites particulières du triangle que l'on connait déjà ! Il suffit d'une petite chasse aux angles pour s'en rendre compte.

On note $H$ l'orthocentre du triangle et $O$ le point d'intersection des "syhauteurs". On a
$$\widehat{OAC} = \widehat{HAB} = 90^\circ - \widehat{ABC},$$ $$\widehat{OCA} = \widehat{HCB} = 90^\circ - \widehat{ABC}.$$ Donc $\widehat{OAC} = \widehat{OCA}$, ce qui signifie que $|OA| = |OC|$. De la même façon, on trouve bien sûr $|OA| = |OB|$ et $|OB| = |OC|$. L'intersection des "syhauteurs" n'est donc rien d'autre que le centre du cercle circonscrit au triangle $ABC$ (et on comprend pourquoi nous avons choisi la notation $O$). Les "syhauteurs" ne sont donc que les droites prolongeant les rayons $OA$, $OB$ et $OC$ du cercle circonscrit à $ABC$.
C'est pour cette raison qu'on ne définit pas les "syhauteurs", mais il est tout de même bon de se souvenir que, dans un triangle $ABC$ d'orthocentre $H$ et de centre du cercle circonscrit $O$, les droites $OA$ et $HA$ sont symétriques par rapport à la bissectrice de $A$ (et de même pour $B$ et $C$).