Théorie > Fondements > Trigonométrie
Degrés et radians
L'unité la plus connue pour la mesure des angles est le degré : un angle droit mesure $90^\circ$, un angle plat mesure $180^\circ$, et un cercle est divisé en $360^\circ$. Il existe cependant une autre unité pour mesurer les angles : le radian. L'idée derrière le radian est que, si on considère un cercle unité (c'est-à-dire de rayon $1$) de centre $O$, alors l'amplitude en radian d'un certain angle $\widehat{AOB}$ avec $A$ et $B$ sur le cercle est exactement égale à la longueur de l'arc que l'angle intercepte.
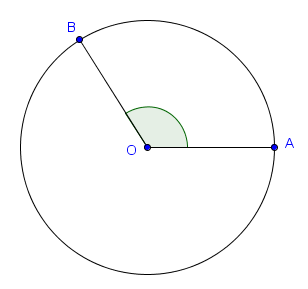
Puisque la circonférence du cercle unité est égale à $2\pi$, on en déduit qu'un angle de $360^\circ$ est de mesure $2 \pi$ radians. Ce qui relie les degrés et les radians est donc l'égalité :
$$\pi \text{ radians} = 180^\circ.$$ Lorsqu'on exprime un angle en radians, on ne note généralement pas l'unité. On dira par exemple qu'un angle droit a une amplitude de $\frac{\pi}{2}$.

Puisque la circonférence du cercle unité est égale à $2\pi$, on en déduit qu'un angle de $360^\circ$ est de mesure $2 \pi$ radians. Ce qui relie les degrés et les radians est donc l'égalité :
$$\pi \text{ radians} = 180^\circ.$$ Lorsqu'on exprime un angle en radians, on ne note généralement pas l'unité. On dira par exemple qu'un angle droit a une amplitude de $\frac{\pi}{2}$.