Théorie > Combinatoire > Pavages
Construction générale
Il arrive aussi qu'il faille donner une façon générale de paver certaines surfaces dont les dimensions sont variables. C'est généralement par une sorte de récurrence que l'on peut donner une telle construction. Illustrons cela avec le problème suivant :
Problème
Pour quels $m, n \in \mathbb{N}_0$ est-il possible de paver (entièrement et sans recouvrement) un rectangle $m \times n$ à l'aide des pavés suivants (pouvant éventuellement être retournés) ?
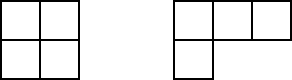
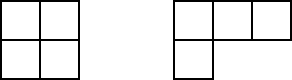
Solution
Vu que les deux pavés contiennent $4$ petits carrés, on voit déjà qu'il faut que $mn$ soit un multiple de $4$ pour avoir une chance que le rectangle $m \times n$ puisse être correctement recouvert. Examinons à présent ces cas où $mn$ est effectivement multiple de $4$
Si $m$ et $n$ sont tous les deux pairs, alors on peut simplement paver le rectangle $m \times n$ grâce aux pavés de forme carrée $2 \times 2$. Le seul cas un peu plus compliqué est donc celui où $m$ est multiple de $4$ et $n$ est impair (ou le contraire, ce cas étant évidemment pareil).
Si $n = 1$, le pavage est bien sûr impossible. Le plus petit cas intéressant est donc le rectangle $4 \times 3$. Après un peu de recherche, on trouve aisément que ce rectangle peut être pavé, par exemple comme suit :
On peut maintenant construire un pavage du rectangle $4 \times n$ pour tout $n$ impair supérieur ou égal à $3$ : il suffit de rajouter des pièces $2 \times 2$ pour compléter le pavage $4 \times 3$ donné ci-dessus. On peut même conclure pour les rectangles $m \times n$ avec $m$ multiple de $4$ et $n$ impair supérieur ou égal à $3$, puisqu'il suffit de mettre côte à côte les pavages trouvés pour un rectangle $4 \times n$.
En conclusion, les seuls rectangles $m \times n$ pour lesquels il n'existe pas de pavage sont ceux avec $mn$ non multiple de $4$ ou ceux avec $m = 1$ ou $n = 1$.
Si $m$ et $n$ sont tous les deux pairs, alors on peut simplement paver le rectangle $m \times n$ grâce aux pavés de forme carrée $2 \times 2$. Le seul cas un peu plus compliqué est donc celui où $m$ est multiple de $4$ et $n$ est impair (ou le contraire, ce cas étant évidemment pareil).
Si $n = 1$, le pavage est bien sûr impossible. Le plus petit cas intéressant est donc le rectangle $4 \times 3$. Après un peu de recherche, on trouve aisément que ce rectangle peut être pavé, par exemple comme suit :
On peut maintenant construire un pavage du rectangle $4 \times n$ pour tout $n$ impair supérieur ou égal à $3$ : il suffit de rajouter des pièces $2 \times 2$ pour compléter le pavage $4 \times 3$ donné ci-dessus. On peut même conclure pour les rectangles $m \times n$ avec $m$ multiple de $4$ et $n$ impair supérieur ou égal à $3$, puisqu'il suffit de mettre côte à côte les pavages trouvés pour un rectangle $4 \times n$.
En conclusion, les seuls rectangles $m \times n$ pour lesquels il n'existe pas de pavage sont ceux avec $mn$ non multiple de $4$ ou ceux avec $m = 1$ ou $n = 1$.