Théorie > Combinatoire > Théorie des graphes

Coloration de graphes

Il arrive que l'on veuille naturellement colorier les différentes arêtes d'un graphe. Considérons par exemple le problème suivant.


Comme suggéré dans une section précédente, on peut écrire ce problème en termes de graphes, en prenant $6$ sommets pour les six étudiants et en reliant deux étudiants dès qu'ils sont amis. Il faut alors prouver que soit il existe un triangle dans le graphe (ce qui signifierait que les étudiants correspondants sont deux à deux amis), soit il existe trois sommets non reliés (ce qui donnerait trois étudiants non amis). La thèse semblait cependant à peu près symétrique au départ et ne l'est plus vraiment en termes de graphes.

Une autre façon de traduire ce problème est de relier toutes les paires de sommets, mais de donner une couleur différente aux arêtes selon que les étudiants concernés sont amis ou non. On peut donc décider de relier des sommets en vert si les étudiants sont amis et en rouge s'ils ne le sont pas. On se retrouve ainsi avec le graphe complet $K_6$ pour lequel chaque arête est coloriée en vert ou en rouge, et le problème consiste à montrer qu'il existe au moins un triangle monochromatique (c'est-à-dire d'une seule couleur) dans le graphe. Sur la figure suivante, on est presque parvenu à trouver un contre-exemple, mais il existe bel et bien un triangle monochromatique (il y en a même deux : un vert et un rouge).



Ce problème est en fait facile à résoudre en faisant bon usage du principe des tiroirs. Procédons par l'absurde en supposant avoir trouvé une coloration de $K_6$ sans aucun triangle monochromatique. On considère alors un sommet quelconque $S$ de ce graphe. De ce sommet partent $5$ arêtes, chacune de couleur verte ou rouge. Par le principe des tiroirs, il y a forcément $3$ de ces arêtes qui sont de la même couleur (on met $5$ chaussettes (les arêtes) dans $2$ tiroirs (les couleurs) : il y a toujours un tiroir contenant $3$ chaussettes). Disons sans perte de généralité que l'on a $3$ arêtes rouges partant de $S$, et qu'elles aboutissent aux sommets $A$, $B$ et $C$. Vu que les arêtes $[S,A]$ et $[S, B]$ sont rouges, l'arête $[A,B]$ est verte (sinon, le triangle $SAB$ serait entièrement rouge). De la même façon, l'arête $[A,C]$ est verte de sorte que $SAC$ ne soit pas entièrement rouge et l'arête $[B, C]$ également de sorte que $SBC$ ne soit pas monochromatique. Mais alors, le triangle $ABC$ est entièrement vert ! Nous avons trouvé une contradiction : il n'est donc pas possible de colorier $K_6$ avec deux couleurs de sorte que l'on ait aucun triangle monochromatique.

Théorème de Ramsey

Ce problème peut être fortement généralisé. On peut en effet considérer le graphe complet $K_N$ pour $N$ quelconque et le colorier avec $c$ couleurs $1, 2, \ldots, c$. Aussi, au lieu de se demander s'il existe un triangle d'une seule couleur, on peut se demander s'il existe un sous-graphe complet $K_{n_i}$ (on parle alors d'une $n_i$-clique) entièrement de la couleur $i$ (pour $n_i$ quelconque dépendant éventuellement de $i$). Notre problème ci-dessus correspondrait alors au cas particulier où $N = 6$, $c = 2$ et $n_1 = n_2 = 3$.

Le théorème de Ramsey nous dit que, quelles que soient les valeurs de $c$ et de $n_1, \ldots, n_c$, il existe toujours un certain $N$ à partir duquel il est impossible de colorier $K_N$ avec $c$ couleurs sans qu'il n'y ait de $n_i$-clique entièrement de la couleur $i$ pour un $i \in \{1, \ldots, c\}$.


Ce résultat se montre par récurrence mais nous ne donnons pas la démonstration ici.

Valeurs des nombres de Ramsey

En montrant que, pour tout coloriage de $K_6$ avec deux couleurs, il existe toujours un triangle monochromatique, on a montré que $R(3,3) \leq 6$. En fait, il n'est pas difficile de montrer qu'on a $R(3,3) = 6$ : il suffit de donner un coloriage de $K_5$ ne contenant aucun triangle monochromatique, comme par exemple le suivant.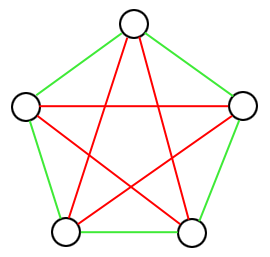


Les nombres de Ramsey ne sont pas bien connus. Par exemple, pour deux couleurs, on ne connait précisément les valeurs de $R(n, m)$ que pour les petites valeurs de $n$ et $m$. Pour des valeurs plus grandes, on ne connait qu'un intervalle dans lequel $R(n, m)$ se situe. En fait, savoir que $R(n, m) \in [a, b]$ signifie deux choses :

• Il existe un coloriage en vert et rouge de $K_{a-1}$ ne contenant aucune $n$-clique entièrement verte et aucune $m$-clique entièrement rouge,
• Il n'existe aucun tel coloriage de $K_b$.

Mais on ne sait pas s'il existe un tel coloriage de $K_x$ pour $x \in [a, b-1]$.