Théorie > Algèbre > Polynômes
Prérequis
Résumé
Nous donnons dans ce chapitre les premières définitions et les premiers résultats concernant les polynômes et leurs racines. Le théorème fondamental de l'algèbre s'intéresse notamment au nombre de racines d'un polynôme à coefficients complexes, et permet l'écriture de tout tel polynôme sous la forme d'un produit plutôt que d'une somme de différents termes.
Ce chapitre a été écrit par N. Radu et mis en ligne le 8 décembre 2014.
1. Définition et divisibilité
Anneaux et corps
Avant de parler de polynômes, nous faisons un petit détour par la définition d'anneau. Celle-ci peut a priori sembler compliquée, mais l'idée est en fait assez simple : il s'agit d'un ensemble $A$ muni d'une opération d'addition $+$ et une opération de multiplication $\cdot$ vérifiant des propriétés naturelles. Par exemple, nous verrons que $\mathbb{R}$ et $\mathbb{Z}$ sont des anneaux. Il n'est pas important de réellement maîtriser cette notion pour passer à la suite : le tout est de comprendre l'idée.Voici tout de même la définition rigoureuse : un anneau est un ensemble $A$ muni de deux opérations binaires : l'addition notée $+$ et la multiplication notée $\cdot$, celles-ci devant vérifier les propriétés suivantes :
- L'addition est associative (c'est-à-dire $(a+b)+c = a+(b+c)$) ;
- L'addition est commutative (c'est-à-dire $a+b = b+a$) ;
- Il existe un zéro (c'est-à-dire un nombre noté $0$ tel que $0 + a = a$ pour tout $a \in A$) ;
- Tout élément de $A$ possède un opposé (c'est-à-dire que pour tout $a \in A$, il existe $b \in A$ tel que $a+b = 0$ : on note alors $b = -a$) ;
- La multiplication est associative (c'est-à-dire $(a\cdot b)\cdot c = a\cdot (b \cdot c)$) ;
- Il existe une unité (c'est-à-dire un nombre noté $1$ tel que $1 \cdot a = a \cdot 1 = a$ pour tout $a \in A$) ;
- La multiplication est distributive par rapport à l'addition (c'est-à-dire $a \cdot (b+c) = a\cdot b + a \cdot c$ et $(a+b) \cdot c = a \cdot c + b \cdot c$).
Il y a donc beaucoup d'hypothèses pour avoir un anneau (commutatif), mais celles-ci sont clairement vérifiées pour certaines structures que l'on connaît déjà.
Exemples :
- $(\mathbb{R}, +, \cdot)$, c'est-à-dire l'ensemble des nombres réels muni de l'addition et de la multiplication usuelle, est un anneau commutatif.
- $(\mathbb{Q}, +, \cdot)$ et $(\mathbb{Z}, +, \cdot)$ sont également des anneaux commutatifs, mais ce n'est pas le cas de $(\mathbb{N}, +, \cdot)$ car les nombres entiers positifs n'ont pas d'opposé dans $\mathbb{N}$.
- $(\mathbb{C}, +, \cdot)$, c'est-à-dire l'ensemble des nombres complexes avec l'addition et la multiplication usuelle, est un anneau commutatif.
- Si on note $\mathbb{Z}/n \mathbb{Z} = \{0, 1, \ldots, n-1\}$ et que l'on considère la somme et le produit modulo $n$, c'est-à-dire la somme et le produit usuel après lesquels on prend le reste de la division par $n$ (voir les chapitres de théorie des nombres), alors $(\mathbb{Z}/n \mathbb{Z}, +, \cdot)$ est un anneau commutatif.
Un corps est enfin un anneau vérifiant une condition supplémentaire : il faut que tout élément non-nul possède un inverse, c'est-à-dire que pour tout $a \in A, a \neq 0$, il existe un certain $b \in A$ tel que $a \cdot b = 1$. Parmi nos exemples, $(\mathbb{R}, +, \cdot)$, $(\mathbb{C}, +, \cdot)$ et $(\mathbb{Q}, +, \cdot)$ sont des corps puisque chaque élément non nul possède un inverse, mais ce n'est par contre pas le cas de $(\mathbb{Z}, +, \cdot)$ car le nombre $2$, par exemple n'a pas d'inverse ($\frac{1}{2}$ n'est pas un nombre entier).
Polynômes
Étant donné un anneau commutatif $A$, nous allons maintenant définir la notion de polynôme sur $A$. Nous considérerons donc toujours dorénavant être en présence d'un anneau commutatif $A$, mais le lecteur non familier avec les anneaux doit simplement penser à $A = \mathbb{R}$ pour se faciliter la lecture, à moins que le contraire ne soit mentionné.Un polynôme sur $A$ est une expression du type
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0,$$ où $n \in \mathbb{N}$ et $c_0, c_1, \ldots, c_n \in A$. Ces éléments sont appelés les coefficients du polynôme; en particulier $c_0$ est appelé terme indépendant. L'élément $x$ est quant à lui la variable. L'ensemble des polynômes sur $A$ est noté $A[x]$.
Le degré du polynôme est le plus grand $m$ tel que $x^m$ apparaît dans l'expression du polynôme. Dans l'expression précédente, le polynôme $P$ est donc de degré $n$ pourvu que $c_n \neq 0$, et le coefficient $c_n$ est dans ce cas appelé coefficient dominant du polynôme. Si $c_n = 1$, ce qui arrive en pratique souvent, le polynôme est dit unitaire.
Remarque : Par convention, le degré du polynôme nul $P(x) = 0$ est égal à $- \infty$.
Exemple : Le polynôme $x^3- x+3$ de $\mathbb{Z}[x]$ est de degré $3$. Son terme indépendant est $3$, alors que son coefficient dominant est $1$ : il s'agit donc d'un polynôme unitaire.
On peut additionner et multiplier des polynômes en utilisant les règles habituelles. En fait, on peut se rendre compte que $(A[x], +, \cdot)$ est lui-même un anneau commutatif, où $+$ et $\cdot$ sont l'addition et la multiplication des polynômes.
Exemple : On a $(x^2+1)+(x+2) = x^2+x+3$ et $(x^2+1) \cdot (x+2) = x^3 + 2x^2 + x + 2$.
Divisibilité
Comme pour les nombres entiers, on peut dire qu'un polynôme en divise un autre. On dit en fait simplement que $Q$ divise $P$ (ou que $P$ est un multiple de $Q$) s'il existe un autre polynôme $R$ tel que$$P = Q \cdot R.$$ Si l'anneau commutatif $A$ sur lequel on considère nos polynômes est en particulier un corps, alors on peut aussi parler du plus grand commun diviseur de deux polynômes $P_1$ et $P_2$. En effet, il existe dans ce contexte un unique polynôme unitaire $D$ tel que $D$ divise $P_1$ et $P_2$ et tel que si un autre polynôme divise $P_1$ et $P_2$, alors il divise $D$.
Deux polynômes sont alors dits premiers entre eux si leur plus grand commun diviseur est le polynôme $D = 1$.
Exemple : Les polynômes $x^2 - 1$ et $x^2+2x+1$ ont pour plus grand commun diviseur le polynôme $x+1$. En effet, on vérifie facilement qu'il divise les deux polynômes et que c'est "le plus grand" diviseur.
Si on est en présence de deux polynômes $P$ et $Q$ sur $K[x]$ où $K$ est un corps commutatif et qu'on désire faire la division euclidienne de $P$ par $Q$, c'est-à-dire trouver des polynômes $D$ et $R$ tels que
$$P = D \cdot Q + R,$$ avec $\deg R < \deg Q$, alors on peut utiliser une méthode très similaire à celle utilisée pour la division des nombres entiers, à l'aide de la méthode de la "potence". Un exemple valant mieux qu'un long discours, on peut par exemple diviser $P(x) = x^4 - 3x^3 + x + 1$ par $D(x) = x^2-2$ comme suit :
$$\begin{array}{cc}
\begin{array}{ccccc}
x^4 & -3x^3 & & +x & +1 \\
x^4 & & -2x^2 & & \\
\hline
& -3x^3 & +2x^2 & +x & +1 \\
& - 3x^3 & & +6x & \\
\hline
& & 2x^2 & -5x & +1 \\
& & 2x^2 & & -4 \\
\hline
& & & -5x &+5
\end{array}
&
\begin{array}{|l}
x^2 - 2\\
\hline
x^2 - 3x + 2 \\ \\
\text{ }\\
\text{ } \\
\text{ } \\
\end{array}
\end{array}$$ Au départ, on choisit $x^2$ car $x^2 \cdot(x^2 - 2)$ possède le même premier terme ($x^4$) que $x^4-3x^3+x+1$, puis on écrit le résultat de $x^2 \cdot (x^2 - 2)$ en dessous de la première ligne et on la soustrait de celle-ci. On est alors en présence d'un nouveau polynôme de plus petit degré : $-3x^3 + 2x^2+x+1$, et on recommence la même opération. On choisit $-3x$ de sorte que $(-3x) \cdot (x^2 - 2)$ ait le même premier terme que ce nouveau polynôme, puis on soustrait le résultat.
À la fin, on note $Q(x) = x^2-3x+2$ et $R(x) = -5x+5$, et on a
$$P = D \cdot Q + R,$$ c'est-à-dire dans notre exemple
$$x^4 - 3x^3 + x + 1 = (x^2 - 2)\cdot (x^2 - 3x+2) + (-5x+5).$$
Lorsque l'on désire trouver le plus grand commun diviseur de deux polynômes, on peut utiliser l'algorithme d'Euclide (voir théorie des nombres). Celui-ci s'applique exactement de la même façon, mis à part qu'il faut effectuer une division (généralement avec potence) à chaque étape, ce qui alourdit significativement le calcul.
2. Racines
Définition de racine
Lorsqu'on a un polynôme de $K[x]$ de la forme$$P(x) = c_n x^n + c_{n-1}x^{n-1}+\ldots + c_1 x + c_0,$$ on peut bien sûr l'évaluer en un élément $a \in K$, en prenant simplement
$$P(a) = c_n a^n + c_{n-1}a^{n-1}+\ldots + c_1 a + c_0.$$ On peut alors définir une racine du polynôme $P$ comme étant un nombre $a \in K$ tel que $P(a) = 0$. On a alors le résultat suivant.
Lemme
Soit $P \in K[x]$ un polynôme (où $K$ est un corps commutatif). Si $a \in K$, alors le reste de la division euclidienne de $P$ par $x-a$ est $P(a)$. En particulier, $a$ est une racine de $P$ si et seulement si $P$ est divisible par $x-a$.
Démonstration
Lorsqu'on effectue la division euclidienne de $P$ par $x-a$, on obtient un reste de degré inférieur à $1$, c'est-à-dire une constante. On a donc
$$P = (x-a) \cdot Q + r,$$ pour un polynôme $Q$ et un élément $r \in K$. En évaluant les deux membres en $x = a$, on voit directement que
$$P(a) = r.$$ De plus, $a$ est une racine de $P$ si et seulement si $0 = P(a) = r$, c'est-à-dire si et seulement si $P$ est divisible par $x-a$.
$$P = (x-a) \cdot Q + r,$$ pour un polynôme $Q$ et un élément $r \in K$. En évaluant les deux membres en $x = a$, on voit directement que
$$P(a) = r.$$ De plus, $a$ est une racine de $P$ si et seulement si $0 = P(a) = r$, c'est-à-dire si et seulement si $P$ est divisible par $x-a$.
Lorsque l'on a une racine $a$ de $P$, on peut donc diviser $P$ par $x-a$ sans qu'il n'y ait de reste. On peut bien sûr utiliser la méthode de la "potence" pour effectuer cette division, mais il existe en fait une méthode plus pratique via le schéma de Horner. Pour diviser le polynôme
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ par $x-a$, on construit le schéma suivant :
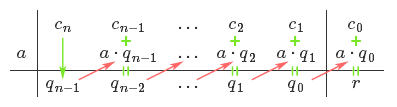
On abaisse d'abord $c_n$ et pose $q_{n-1} = c_n$. On multiplie ensuite $q_{n-1}$ par $a$ et écrit le résultat en dessous de $c_{n-1}$. On pose alors $q_{n-2} = c_{n-1} + a\cdot q_{n-1}$, et continue ce processus jusqu'au bout du tableau. À la fin, on note $r$ le dernier élément obtenu et celui-ci sera toujours égal au reste de la division, c'est-à-dire à $P(a)$ (dans le cas contraire, c'est qu'une erreur a été commise). Le polynôme quotient est quand à lui donné par
$$Q(x) = q_{n-1} x^{n-1} + \ldots + q_1 x + q_0.$$ Montrer que cette méthode donne bien le bon résultat est un simple exercice.
Racine multiple
Le polynôme $P(x) = x^3 - 4x^2 + 4x = x(x-2)^2$ a évidemment $2$ pour racine. Par ailleurs, on voit que $x-2$ divise bien $P$, conformément au résultat précédent. Intuitivement, il semble qu'on ait même un peu mieux qu'une racine, puisque $x-2$ divise "deux fois" $P$, au sens où $(x-2)^2$ le divise. Dans un tel cas, on dit en fait que $2$ est une racine double du polynôme, ou encore qu'il s'agit d'une racine de multiplicité $2$.De manière générale, on définit la multiplicité d'une racine $a$ de $P$ comme étant le plus grand naturel $m$ tel que $(x-a)^m$ divise $P$. Un nombre qui n'est pas une racine de $P$ peut donc être considéré comme une racine de multiplicité nulle.
Pour le résultat suivant, on a besoin de la notion de polynôme dérivé. Pour ceux qui connaissent les dérivées, il s'agit simplement de la dérivée du polynôme. Cela dit, on peut simplement définir le polynôme dérivé de
$$P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$$ comme étant le polynôme
$$P'(x) = nc_n x^{n-1} + (n-1) c_{n-1} x^{n-2} + \ldots + c_1$$ (pour chaque terme, on "abaisse" l'exposant de $x$ en le mettant devant le coefficient et on diminue cet exposant de $1$). On peut itérer la dérivée et on parle alors de dérivée seconde $P''$ lorsque l'on dérive $P$ deux fois consécutivement, tout comme la dérivée $k$-ème notée $P^{(k)}$ qui est le résultat de $k$ dérivations successives.
Proposition
Soit $P \in K[x]$ un polynôme. Un élément $a \in K$ est une racine de $P$ de multiplicité $m \in \mathbb{N}$ si et seulement si
$$P(a) = P'(a) = \ldots = P^{(m-1)}(a) = 0$$ mais $P^{(m)}(a) \neq 0$.
$$P(a) = P'(a) = \ldots = P^{(m-1)}(a) = 0$$ mais $P^{(m)}(a) \neq 0$.
Nous ne démontrons pas ce résultat mais l'illustrons sur l'exemple précédemment donné $P(x) = x^3 - 4x^2 + 4x$. Calculons d'abord ses dérivées successives :
$$P'(x) = 3x^2 - 8x + 4,$$ $$P''(x) = 6x - 8,$$ $$P^{(3)}(x) = 6,$$ $$P^{(4)}(x) = 0.$$ Évaluons alors $P$ et ses différentes dérivées en $a = 2$ :
$$P(2) = 2^3 - 4\cdot 2^2+4\cdot 2 = 8-16+8=0,$$ $$P'(2) = 3\cdot 2^2 - 8 \cdot 2 + 4 = 12 - 16 + 4 = 0,$$ $$P''(2) = 6\cdot 2 - 8 = 12 - 8 = 4.$$ Par le résultat précédent, $2$ est donc une racine de multiplicité $2$ de $P$, ce que nous avions bien observé par définition de multiplicité puisque $P(x) = x(x-2)^2$.
3. Second degré
Il n'est en général pas facile de trouver les racines d'un polynôme quelconque. Cela dit, il est tout de même possible de déterminer les racines d'un polynôme de degré $2$ (cela étant trivial pour les polynômes de degré $1$). Nous donnons le résultat pour les polynômes à coefficients complexes, mais il est en fait également vrai sur un corps commutatif quelconque (sous certaines conditions).
Il existe aussi des formules (ou plutôt des méthodes) pour trouver les racines d'un polynôme de degré $3$ ou $4$. Celles-ci sont cependant beaucoup plus compliquées que celle pour le second degré, et cela ne vaut pas la peine de les connaître. Un résultat remarquable dû aux travaux de Galois est qu'il n'existe en fait pas de formule ou méthode générale pour trouver les racines d'un polynôme de degré supérieur ou égal à $5$. Par exemple, on peut montrer qu'il n'est pas possible d'exprimer les racines du polynôme $P(x) = x^5 - 3x - 1$ à l'aide des opérations usuelles et de radicaux.
Proposition
Soit $P(x) = ax^2 + bx + c$ un polynôme de $\mathbb{C}[x]$ de degré $2$ (c'est-à-dire avec $a \neq 0$). Les racines de $P$ sont données par
$$\frac{-b + \delta}{2a} \quad \text{et} \quad \frac{-b - \delta}{2a},$$ où $\delta$ est une racine carrée (éventuellement complexe) de $\Delta := b^2 - 4ac$, appelé discriminant.
$$\frac{-b + \delta}{2a} \quad \text{et} \quad \frac{-b - \delta}{2a},$$ où $\delta$ est une racine carrée (éventuellement complexe) de $\Delta := b^2 - 4ac$, appelé discriminant.
Démonstration
L'idée est de faire apparaître un carré parfait. Pour cela, on écrit
$$\begin{align}
P(x) &= ax^2 + bx + c \\
&= a\left(x^2 + \frac{b}{a} x + \frac{c}{a}\right) \\
&= a\left(x^2 + 2\cdot\frac{b}{2a}\cdot x + \left(\frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{c}{a}\right) \\
&= a\left(\left(x + \frac{b}{2a}\right)^2 - \frac{b^2 -4ac}{4a^2} \right).
\end{align}$$ Le nombre $b^2 - 4ac$, que l'on appelle discriminant, est un nombre complexe. Il possède donc deux racines carrées (ou une s'il est nul) et on en note une $\delta$. On peut alors continuer notre raisonnement :
$$\begin{align}
P(x) &= a\left(\left(x + \frac{b}{2a}\right)^2 - \frac{\delta^2}{4a^2} \right)\\
&= a\left(x + \frac{b}{2a} + \frac{\delta}{2a} \right) \left(x + \frac{b}{2a} - \frac{\delta}{2a} \right)\\
&= a\left(x - \frac{-b-\delta}{2a} \right) \left(x - \frac{-b+\delta}{2a} \right)
\end{align}$$ On a donc $P(x) = 0$ si et seulement si $x$ est d'une des deux formes de l'énoncé.
$$\begin{align}
P(x) &= ax^2 + bx + c \\
&= a\left(x^2 + \frac{b}{a} x + \frac{c}{a}\right) \\
&= a\left(x^2 + 2\cdot\frac{b}{2a}\cdot x + \left(\frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{c}{a}\right) \\
&= a\left(\left(x + \frac{b}{2a}\right)^2 - \frac{b^2 -4ac}{4a^2} \right).
\end{align}$$ Le nombre $b^2 - 4ac$, que l'on appelle discriminant, est un nombre complexe. Il possède donc deux racines carrées (ou une s'il est nul) et on en note une $\delta$. On peut alors continuer notre raisonnement :
$$\begin{align}
P(x) &= a\left(\left(x + \frac{b}{2a}\right)^2 - \frac{\delta^2}{4a^2} \right)\\
&= a\left(x + \frac{b}{2a} + \frac{\delta}{2a} \right) \left(x + \frac{b}{2a} - \frac{\delta}{2a} \right)\\
&= a\left(x - \frac{-b-\delta}{2a} \right) \left(x - \frac{-b+\delta}{2a} \right)
\end{align}$$ On a donc $P(x) = 0$ si et seulement si $x$ est d'une des deux formes de l'énoncé.
Il existe aussi des formules (ou plutôt des méthodes) pour trouver les racines d'un polynôme de degré $3$ ou $4$. Celles-ci sont cependant beaucoup plus compliquées que celle pour le second degré, et cela ne vaut pas la peine de les connaître. Un résultat remarquable dû aux travaux de Galois est qu'il n'existe en fait pas de formule ou méthode générale pour trouver les racines d'un polynôme de degré supérieur ou égal à $5$. Par exemple, on peut montrer qu'il n'est pas possible d'exprimer les racines du polynôme $P(x) = x^5 - 3x - 1$ à l'aide des opérations usuelles et de radicaux.
4. Théorème fondamental
Dans cette partie nous ne considérons que des polynômes non-nuls.
Exemple :
On a donc un maximum de $n$ racines pour un polynôme de degré $n$, et il arrive qu'il y en ait moins. Remarquons tout de même que, dans le deuxième exemple, si on avait considéré le polynôme comme étant dans $\mathbb{C}[x]$, alors il aurait eu $3$ racines puisque $Q(x) = x(x+i)(x-i)$. Le théorème fondamental de l'algèbre nous apprend en fait que dans $\mathbb{C}[x]$, tous les polynômes ont un nombre de racines exactement égal à leur degré.
Si on ne considère pas $P \in \mathbb{C}[x]$ mais plutôt $P \in \mathbb{R}[x]$ ou $P \in \mathbb{Z}[x]$, alors le théorème fondamental peut tout de même être utile ! En effet, on a $\mathbb{Z} \subset \mathbb{R} \subset \mathbb{C}$ donc un polynôme à coefficients réels (ou entiers) peut très bien être pensé comme un polynôme à coefficients complexes. On peut donc aussi l'écrire comme produit de $(x-r_i)$, mais il faut bien se rappeler qu'il est fort probable que certaines des racines $r_i$ soient complexes.
Remarque :
On peut faire le lien entre la forme usuelle des polynômes et cette nouvelle forme. On a en effet
$$c_n x^n + c_{n-1}x^{n-1} + \ldots + c_1 x + c_0 = c_n(x-r_1)(x-r_2)\ldots(x-r_n).$$ Si nous effectuons le produit du membre de droite, alors en regardant les coefficients de $x^{n-1}$ ainsi que les termes indépendants, on voit que
$$c_{n-1} = c_n \cdot (-r_1-r_2-\ldots-r_n) \quad \text{et} \quad c_0 = (-1)^n \cdot c_n \cdot r_1r_2 \ldots r_n.$$ Cela signifie que, lorsqu'on a un polynôme sous sa forme usuelle, on peut directement connaître la somme et le produit des $n$ racines puisque
$$r_1+r_2+\ldots+r_n = -\frac{c_{n-1}}{c_n} \quad \text{et} \quad r_1r_2\ldots r_n = (-1)^n\cdot \frac{c_0}{c_n}.$$ En regardant les autres coefficients comme $c_{n-2}$, on peut trouver d'autres formules un peu plus compliquées reliant les racines aux coefficients usuels : celles-ci peuvent également se révéler utiles, elles s'appellent formules de Viète et nous en reparlerons dans un futur chapitre.
Par exemple, le graphe du polynôme $P(x) = 2x^5 -8x+2$ est le suivant.
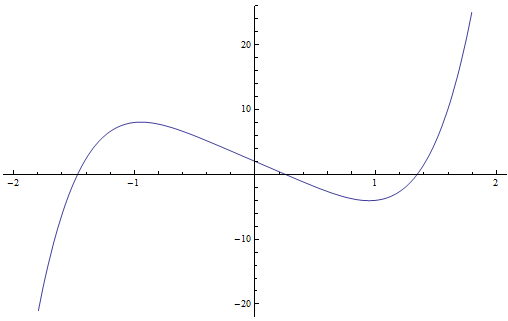
On observe que ce polynôme possède trois racines réelles puisque le graphe traverse trois fois l'axe des abscisses. (Aucune des racines réelles n'est multiple : une racine multiple se repère au fait que le graphe est alors tangent à l'axe des abscisses en le point concerné.) Comme le polynôme est de degré $5$, on sait par le théorème fondamental qu'il a aussi deux racines complexes.
A priori, on ne sait rien de ces racines complexes, mais il existe en fait un résultat intéressant : les racines complexes vont deux par deux en ce sens que si $z$ est une racine de $P$, alors son conjugué $\bar z$ également. Il est important que le polynôme soit à coefficient réels (et non complexes) pour que ce résultat soit vérifié.
Ce résultat peut paraître anodin, mais est en fait très utile. En effet, cela signifie que dans la décomposition de $P(x)$ en produit de $(x-r_i)$, chaque $r_i$ est soit réel, soit complexe auquel cas on a aussi $(x-\bar r_i)$. Vu que les multiplicités de deux racines conjuguées sont identiques, le terme $(x-r_i)$ apparaît le même nombre de fois que $(x-\bar r_i)$, ce qui signifie qu'on peut les rassembler deux par deux. Cela est intéressant car on a
$$(x-r_i)(x-\bar r_i) = x^2 - (r_i + \bar r_i) x + r_i \bar r_i = x^2 - 2\cdot\mathfrak{Re}(r_i) x + |r_i|^2,$$ et ce polynôme a des coefficients réels puisque la partie réelle et le module d'un complexe sont des nombres réels. On a donc démontré le résultat suivant :
Par polynôme irréductible, il faut ici simplement comprendre que les polynômes $Q_i$ n'ont pas de racines réelles (on ne peut donc pas les réduire en un produit de $(x-r_i)$ avec $r_i \in \mathbb{R}$). Autrement dit, chaque polynôme $Q_i$ a un discriminant strictement négatif.
Remarque : Une conséquence directe de ce résultat est que le nombre de racines réelles (comptées avec leur multiplicité) d'un polynôme de degré $n$ est de la même parité que $n$. En particulier, un polynôme de degré impair possède toujours au moins une racine réelle. Cela peut également être compris en examinant le graphe d'un tel polynôme, puisque celui-ci arrive de la gauche par le bas et repart vers la droite par le haut (ou le contraire si le coefficient dominant est négatif). Le graphe coupe donc l'axe réel un nombre impair de fois.
Lorsqu'on est en présence d'un polynôme dans un problème d'algèbre, il peut être bon d'écrire celui-ci sous cette forme (avec les $r_i$ et $Q_i$ inconnus). L'avantage de celle-ci sur celle avec uniquement les $n$ racines est qu'elle ne fait pas intervenir de nombres complexes. On peut donc par exemple mieux maîtriser le signe de $P$ en fonction des $r_i$ et $Q_i$, ce qui n'est pas possible quand on travaille avec des nombres complexes.
Nombre de racines
Puisqu'à chaque fois que $a$ est une racine de multiplicité $m$ d'un polynôme, on peut diviser celui-ci par $(x-a)^m$, il en découle que le nombre de racines (comptées avec leur multiplicité) d'un polynôme de degré $n$ est toujours inférieur ou égal à $n$.Exemple :
- Le polynôme $P(x) = x^3-4x^2+5x-2$ de $\mathbb{R}[x]$ a trois racines (comptées avec leur multiplicité) : la racine double $1$ et la racine simple $2$; et ce parce que $P(x) = (x-1)^2(x-2)$.
- Le polynôme $Q(x) = x^3 + x$ de $\mathbb{R}[x]$ a quant à lui une seule racine (et elle est simple) : $x = 0$. En effet, $Q(x) = x(x^2+1)$ et le polynôme $x^2+1$ n'a pas de racines réelles.
On a donc un maximum de $n$ racines pour un polynôme de degré $n$, et il arrive qu'il y en ait moins. Remarquons tout de même que, dans le deuxième exemple, si on avait considéré le polynôme comme étant dans $\mathbb{C}[x]$, alors il aurait eu $3$ racines puisque $Q(x) = x(x+i)(x-i)$. Le théorème fondamental de l'algèbre nous apprend en fait que dans $\mathbb{C}[x]$, tous les polynômes ont un nombre de racines exactement égal à leur degré.
Théorème fondamental de l'algèbre
Soit $P \in \mathbb{C}[x]$ un polynôme de degré $n \in \mathbb{N}$. Alors $P$ possède exactement $n$ racines comptées avec leur multiplicité. Autrement dit, il existe des nombres $r_1, r_2, \ldots, r_n \in \mathbb{C}$ tels que
$$P(x) = c_n(x-r_1)(x-r_2)\ldots(x-r_n),$$ où $c_n$ est le coefficient dominant de $P$.
$$P(x) = c_n(x-r_1)(x-r_2)\ldots(x-r_n),$$ où $c_n$ est le coefficient dominant de $P$.
Si on ne considère pas $P \in \mathbb{C}[x]$ mais plutôt $P \in \mathbb{R}[x]$ ou $P \in \mathbb{Z}[x]$, alors le théorème fondamental peut tout de même être utile ! En effet, on a $\mathbb{Z} \subset \mathbb{R} \subset \mathbb{C}$ donc un polynôme à coefficients réels (ou entiers) peut très bien être pensé comme un polynôme à coefficients complexes. On peut donc aussi l'écrire comme produit de $(x-r_i)$, mais il faut bien se rappeler qu'il est fort probable que certaines des racines $r_i$ soient complexes.
Remarque :
On peut faire le lien entre la forme usuelle des polynômes et cette nouvelle forme. On a en effet
$$c_n x^n + c_{n-1}x^{n-1} + \ldots + c_1 x + c_0 = c_n(x-r_1)(x-r_2)\ldots(x-r_n).$$ Si nous effectuons le produit du membre de droite, alors en regardant les coefficients de $x^{n-1}$ ainsi que les termes indépendants, on voit que
$$c_{n-1} = c_n \cdot (-r_1-r_2-\ldots-r_n) \quad \text{et} \quad c_0 = (-1)^n \cdot c_n \cdot r_1r_2 \ldots r_n.$$ Cela signifie que, lorsqu'on a un polynôme sous sa forme usuelle, on peut directement connaître la somme et le produit des $n$ racines puisque
$$r_1+r_2+\ldots+r_n = -\frac{c_{n-1}}{c_n} \quad \text{et} \quad r_1r_2\ldots r_n = (-1)^n\cdot \frac{c_0}{c_n}.$$ En regardant les autres coefficients comme $c_{n-2}$, on peut trouver d'autres formules un peu plus compliquées reliant les racines aux coefficients usuels : celles-ci peuvent également se révéler utiles, elles s'appellent formules de Viète et nous en reparlerons dans un futur chapitre.
Polynômes à coefficients réels
Comme nous venons de l'expliquer, le théorème fondamental de l'algèbre est également utile même lorsque $P$ est à coefficients réels. Il est alors assez naturel de distinguer les racines réelles de $P$ des racines complexes. En fait, lorsqu'on dessine le graphe d'un polynôme à coefficients réels, on peut facilement observer où se situent les racines réelles, mais les racines complexes ne sont par contre pas détectables.Par exemple, le graphe du polynôme $P(x) = 2x^5 -8x+2$ est le suivant.
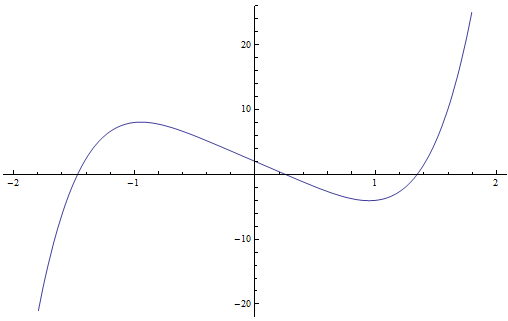
On observe que ce polynôme possède trois racines réelles puisque le graphe traverse trois fois l'axe des abscisses. (Aucune des racines réelles n'est multiple : une racine multiple se repère au fait que le graphe est alors tangent à l'axe des abscisses en le point concerné.) Comme le polynôme est de degré $5$, on sait par le théorème fondamental qu'il a aussi deux racines complexes.
A priori, on ne sait rien de ces racines complexes, mais il existe en fait un résultat intéressant : les racines complexes vont deux par deux en ce sens que si $z$ est une racine de $P$, alors son conjugué $\bar z$ également. Il est important que le polynôme soit à coefficient réels (et non complexes) pour que ce résultat soit vérifié.
Lemme
Soit $P \in \mathbb{R}[x]$ un polynôme. Si $z \in \mathbb{C}$ est une racine de $P$ de multiplicité $m$, alors $\bar z$ est aussi une racine de $P$ de multiplicité $m$.
Démonstration
Notons $P(x) = c_n x^n + c_{n-1} x^{n-1} + \ldots + c_1 x + c_0$, où les coefficients $c_i$ sont réels. Le fait que $P(z) = 0$ signifie que
$$c_n z^n + c_{n-1} z^{n-1} + \ldots + c_1 z + c_0 = 0.$$ On peut alors simplement prendre le conjugué des deux membres pour obtenir (rappelons que le conjugué d'un produit est égal au produit des conjugués, et de même pour la somme) :
$$\bar c_n \bar z^n + \bar c_{n-1} \bar z^{n-1} + \ldots + \bar c_1 \bar z + \bar c_0 = 0$$ Or, les coefficients étant réels, on a $\bar c_i = c_i$ pour tout $i$, et donc
$$c_n \bar z^n + c_{n-1} \bar z^{n-1} + \ldots + c_1 \bar z + c_0 = 0,$$ ce qui est exactement $P(\bar z) = 0$. Si maintenant $z$ est une racine double, on a $P'(z) = 0$ et par le même raisonnement on trouve $P'(\bar z) = 0$. On en déduit ainsi que la multiplicité de $z$ est la même que celle de $\bar z$.
$$c_n z^n + c_{n-1} z^{n-1} + \ldots + c_1 z + c_0 = 0.$$ On peut alors simplement prendre le conjugué des deux membres pour obtenir (rappelons que le conjugué d'un produit est égal au produit des conjugués, et de même pour la somme) :
$$\bar c_n \bar z^n + \bar c_{n-1} \bar z^{n-1} + \ldots + \bar c_1 \bar z + \bar c_0 = 0$$ Or, les coefficients étant réels, on a $\bar c_i = c_i$ pour tout $i$, et donc
$$c_n \bar z^n + c_{n-1} \bar z^{n-1} + \ldots + c_1 \bar z + c_0 = 0,$$ ce qui est exactement $P(\bar z) = 0$. Si maintenant $z$ est une racine double, on a $P'(z) = 0$ et par le même raisonnement on trouve $P'(\bar z) = 0$. On en déduit ainsi que la multiplicité de $z$ est la même que celle de $\bar z$.
Ce résultat peut paraître anodin, mais est en fait très utile. En effet, cela signifie que dans la décomposition de $P(x)$ en produit de $(x-r_i)$, chaque $r_i$ est soit réel, soit complexe auquel cas on a aussi $(x-\bar r_i)$. Vu que les multiplicités de deux racines conjuguées sont identiques, le terme $(x-r_i)$ apparaît le même nombre de fois que $(x-\bar r_i)$, ce qui signifie qu'on peut les rassembler deux par deux. Cela est intéressant car on a
$$(x-r_i)(x-\bar r_i) = x^2 - (r_i + \bar r_i) x + r_i \bar r_i = x^2 - 2\cdot\mathfrak{Re}(r_i) x + |r_i|^2,$$ et ce polynôme a des coefficients réels puisque la partie réelle et le module d'un complexe sont des nombres réels. On a donc démontré le résultat suivant :
Théorème fondamental de l'algèbre pour les polynômes à coefficients réels
Soit $P \in \mathbb{R}[x]$ un polynôme de degré $n$. Il existe $k$ nombres réels $r_1, \ldots, r_k$ et $l$ polynômes $Q_1, \ldots, Q_l \in \mathbb{R}[x]$ unitaires irréductibles du second degré avec $k+2l = n$ tels que
$$P(x) = c_n(x-r_1)\ldots (x-r_k)Q_1(x)\ldots Q_l(x),$$ où $c_n$ est le coefficient dominant de $P$.
$$P(x) = c_n(x-r_1)\ldots (x-r_k)Q_1(x)\ldots Q_l(x),$$ où $c_n$ est le coefficient dominant de $P$.
Par polynôme irréductible, il faut ici simplement comprendre que les polynômes $Q_i$ n'ont pas de racines réelles (on ne peut donc pas les réduire en un produit de $(x-r_i)$ avec $r_i \in \mathbb{R}$). Autrement dit, chaque polynôme $Q_i$ a un discriminant strictement négatif.
Remarque : Une conséquence directe de ce résultat est que le nombre de racines réelles (comptées avec leur multiplicité) d'un polynôme de degré $n$ est de la même parité que $n$. En particulier, un polynôme de degré impair possède toujours au moins une racine réelle. Cela peut également être compris en examinant le graphe d'un tel polynôme, puisque celui-ci arrive de la gauche par le bas et repart vers la droite par le haut (ou le contraire si le coefficient dominant est négatif). Le graphe coupe donc l'axe réel un nombre impair de fois.
Lorsqu'on est en présence d'un polynôme dans un problème d'algèbre, il peut être bon d'écrire celui-ci sous cette forme (avec les $r_i$ et $Q_i$ inconnus). L'avantage de celle-ci sur celle avec uniquement les $n$ racines est qu'elle ne fait pas intervenir de nombres complexes. On peut donc par exemple mieux maîtriser le signe de $P$ en fonction des $r_i$ et $Q_i$, ce qui n'est pas possible quand on travaille avec des nombres complexes.