Théorie > Géométrie > Solutions non classiques
IMO 2009
Voici le problème 4 de l'IMO 2009 :
Encore une fois, ce problème possède une solution "classique", mais la plupart des participants à l'IMO cette année-là l'ont en fait résolu avec de la trigonométrie. Il n'est toutefois pas évident de savoir par où commencer, et il faut à tout prix éviter de tourner en rond.
Problème (IMO 2009, P4)
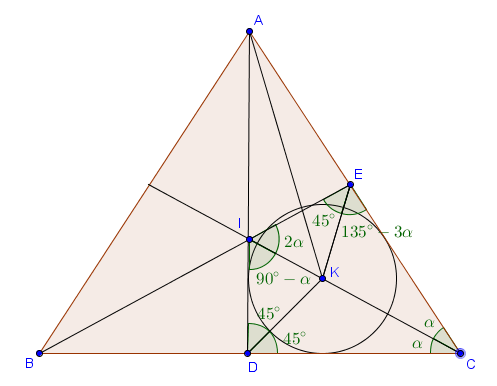
Soit $ABC$ un triangle tel que $|AB| = |AC|$. Les bissectrices de $\widehat{CAB}$ et $\widehat{ABC}$ rencontrent respectivement les côtés $[BC]$ et $[CA]$ en $D$ et $E$. Soit $K$ le centre du cercle inscrit dans le triangle $ADC$. On suppose que $\widehat{BEK} = 45^\circ$. Trouver toutes les valeurs possibles de $\widehat{CAB}$.
Encore une fois, ce problème possède une solution "classique", mais la plupart des participants à l'IMO cette année-là l'ont en fait résolu avec de la trigonométrie. Il n'est toutefois pas évident de savoir par où commencer, et il faut à tout prix éviter de tourner en rond.
Solution trigonométrique
Notons $I$ l'intersection des bissectrices de $ABC$. Les points $C$, $K$ et $I$ sont alignés. Posons également $\alpha = \widehat{ICD}$. Nous allons appliquer la loi des sinus dans les triangles $DIK$, $KIE$, $EKC$ et $CKD$. Pour cela, il faut exprimer tous les angles intervenant dans ces triangles en fonction de $\alpha$.
Appliquons maintenant nos lois des sinus :
$$\sin(90^\circ-\alpha)\cdot \sin 45^\circ\cdot \sin \alpha\cdot \sin 45^\circ = \sin 45^\circ\cdot \sin 2\alpha\cdot \sin(135^\circ-3\alpha)\cdot \sin \alpha,$$ ce qui se réécrit encore en utilisant que $\sin(90^\circ - \alpha) = \cos \alpha$ et que $\sin2\alpha = 2 \sin \alpha \cos \alpha$ :
$$\sin 45^\circ = 2 \sin \alpha \cdot \sin(135^\circ-3\alpha).$$ Puisque $\sin(135^\circ - 3\alpha) = \sin(45^\circ + 3\alpha) = \sin 45^\circ \cdot \cos 3\alpha + \cos 45^\circ \cdot \sin 3\alpha = \sin 45^\circ \cdot (\cos 3\alpha + \sin 3\alpha)$, l'équation se réécrit encore
$$1 = 2\sin \alpha \cdot (\cos 3 \alpha + \sin 3 \alpha).$$ Il nous reste à résoudre cette équation trigonométrique en $\alpha$. Il y a plusieurs façons de procéder, voici une manière.
On peut développer $\cos 3\alpha = \cos (2\alpha+\alpha)$ et $\sin 3 \alpha = \sin(2\alpha+\alpha)$. L'équation devient
$$\begin{align}
1 &= 2 \sin \alpha \cdot (\cos 2\alpha \cos \alpha - \sin 2\alpha \sin \alpha + \sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha)\\
&= 2 \sin \alpha \cdot \cos \alpha \cdot (\cos 2\alpha + \sin 2\alpha) + 2\sin^2 \alpha \cdot (\cos 2\alpha - \sin 2\alpha)\\
\end{align}$$ Or, on a $2 \sin \alpha \cos \alpha = \sin 2\alpha$ et $2 \sin^2\alpha = 1 - \cos 2 \alpha$, donc
$$\begin{align}
&1 = \sin 2\alpha \cdot (\cos 2\alpha + \sin 2\alpha) + (1 - \cos 2\alpha) \cdot (\cos 2\alpha - \sin 2\alpha)\\
\Leftrightarrow \ & 1 = 2 \sin 2\alpha \cos 2\alpha + \sin^2 2\alpha - \cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = 2 \sin 2\alpha \cos 2\alpha - 2\cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = (2 \cos 2 \alpha - 1)(\sin 2\alpha - \cos 2\alpha)
\end{align}$$ On en déduit que $\alpha$ doit respecter $\cos 2\alpha = \frac{1}{2}$ ou $\cos 2\alpha = \sin 2\alpha$ pour pouvoir respecter les conditions de l'énoncé. La première équation donne $2\alpha = 60^\circ$ et la deuxième donne $2\alpha = 45^\circ$. Puisque $\widehat{BAC} = 180^\circ-4\alpha$, cet angle doit valoir $60^\circ$ ou $90^\circ$. Il est important de noter que, tout comme pour une équation fonctionnelle, il faut ici vérifier que ces deux angles $60^\circ$ et $90^\circ$ donnent bien lieu à $\widehat{BEK} = 45^\circ$. Nous ne nous étendons pas sur ce point car c'est un simple exercice, mais les distraits ayant oublié cette vérification en 2009 se sont vu attribuer un score de $5/7$ pour cette question.
- $\widehat{KCE} = \alpha$
- $\widehat{KCD} = \alpha$
- $\widehat{KDC} = 45^\circ$
- $\widehat{KDI} = 45^\circ$
- $\widehat{KID} = \widehat{CID} = 90^\circ - \widehat{ICD} = 90^\circ - \alpha$
- $\widehat{KIE} = 180^\circ - \widehat{BID} - \widehat{DIK} = 180^\circ - (90^\circ-\alpha) - (90^\circ-\alpha) = 2\alpha$
- $\widehat{KEI} = 45^\circ$ (par hypothèse)
- $\widehat{KEC} = \widehat{BEC} - \widehat{BEK} = 180^\circ - 3\alpha - 45^\circ = 135^\circ - 3\alpha$

Appliquons maintenant nos lois des sinus :
- Dans le triangle $DIK$, on obtient
$$\frac{|IK|}{\sin 45^\circ} = \frac{|DK|}{\sin(90^\circ - \alpha)}$$ - Dans le triangle $KIE$, on obtient
$$\frac{|EK|}{\sin 2\alpha} = \frac{|IK|}{\sin 45^\circ}$$ - Dans le triangle $EKC$, on obtient
$$\frac{|CK|}{\sin(135^\circ-3\alpha)} = \frac{|EK|}{\sin \alpha}$$ - Dans le triangle $CKD$, on obtient
$$\frac{|DK|}{\sin\alpha} = \frac{|CK|}{\sin 45^\circ}$$
$$\sin(90^\circ-\alpha)\cdot \sin 45^\circ\cdot \sin \alpha\cdot \sin 45^\circ = \sin 45^\circ\cdot \sin 2\alpha\cdot \sin(135^\circ-3\alpha)\cdot \sin \alpha,$$ ce qui se réécrit encore en utilisant que $\sin(90^\circ - \alpha) = \cos \alpha$ et que $\sin2\alpha = 2 \sin \alpha \cos \alpha$ :
$$\sin 45^\circ = 2 \sin \alpha \cdot \sin(135^\circ-3\alpha).$$ Puisque $\sin(135^\circ - 3\alpha) = \sin(45^\circ + 3\alpha) = \sin 45^\circ \cdot \cos 3\alpha + \cos 45^\circ \cdot \sin 3\alpha = \sin 45^\circ \cdot (\cos 3\alpha + \sin 3\alpha)$, l'équation se réécrit encore
$$1 = 2\sin \alpha \cdot (\cos 3 \alpha + \sin 3 \alpha).$$ Il nous reste à résoudre cette équation trigonométrique en $\alpha$. Il y a plusieurs façons de procéder, voici une manière.
On peut développer $\cos 3\alpha = \cos (2\alpha+\alpha)$ et $\sin 3 \alpha = \sin(2\alpha+\alpha)$. L'équation devient
$$\begin{align}
1 &= 2 \sin \alpha \cdot (\cos 2\alpha \cos \alpha - \sin 2\alpha \sin \alpha + \sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha)\\
&= 2 \sin \alpha \cdot \cos \alpha \cdot (\cos 2\alpha + \sin 2\alpha) + 2\sin^2 \alpha \cdot (\cos 2\alpha - \sin 2\alpha)\\
\end{align}$$ Or, on a $2 \sin \alpha \cos \alpha = \sin 2\alpha$ et $2 \sin^2\alpha = 1 - \cos 2 \alpha$, donc
$$\begin{align}
&1 = \sin 2\alpha \cdot (\cos 2\alpha + \sin 2\alpha) + (1 - \cos 2\alpha) \cdot (\cos 2\alpha - \sin 2\alpha)\\
\Leftrightarrow \ & 1 = 2 \sin 2\alpha \cos 2\alpha + \sin^2 2\alpha - \cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = 2 \sin 2\alpha \cos 2\alpha - 2\cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = (2 \cos 2 \alpha - 1)(\sin 2\alpha - \cos 2\alpha)
\end{align}$$ On en déduit que $\alpha$ doit respecter $\cos 2\alpha = \frac{1}{2}$ ou $\cos 2\alpha = \sin 2\alpha$ pour pouvoir respecter les conditions de l'énoncé. La première équation donne $2\alpha = 60^\circ$ et la deuxième donne $2\alpha = 45^\circ$. Puisque $\widehat{BAC} = 180^\circ-4\alpha$, cet angle doit valoir $60^\circ$ ou $90^\circ$. Il est important de noter que, tout comme pour une équation fonctionnelle, il faut ici vérifier que ces deux angles $60^\circ$ et $90^\circ$ donnent bien lieu à $\widehat{BEK} = 45^\circ$. Nous ne nous étendons pas sur ce point car c'est un simple exercice, mais les distraits ayant oublié cette vérification en 2009 se sont vu attribuer un score de $5/7$ pour cette question.