Théorie > Géométrie > Solutions non classiques
Prérequis
Résumé
La géométrie analytique et la trigonométrie peuvent permettre de résoudre certains problèmes de manière moins conventionnelle. Les solutions obtenues sont alors assez laborieuses, c'est pourquoi il ne faut envisager ces méthodes qu'en dernier recours.
Ce chapitre a été écrit par N. Radu et mis en ligne le 20 juillet 2016.
1. Géométrie analytique
La géométrie analytique consiste à choisir un repère (généralement orthonormé) intéressant, c'est-à-dire donner l'origine du repère et ses deux axes, et à calculer les coordonnées des points et les équations des droites et des cercles qui nous intéressent. Par exemple, s'il est demandé de prouver qu'un certain point appartient à une certaine droite, on peut être tenté de calculer les coordonnées du point, une équation de la droite et simplement montrer que les coordonnées du point vérifient l'équation.
Bien sûr, il y a souvent des libertés dans la figure et il faudra alors faire usage de paramètres pour procéder de cette façon. Si on est en présence d'un triangle $ABC$, on peut par exemple poser l'origine du repère en $A$ et pointer l'axe des abscisses vers $B$. De la sorte, les coordonnées de $A$ sont $(0,0)$, les coordonnées de $B$ sont $(b,0)$ pour un certain $b > 0$, et les coordonnées de $C$ sont $(c_1,c_2)$ pour certains $c_1, c_2$. On peut éventuellement se simplifier la vie en posant $|AB| = 1$, de sorte que $b = 1$ (mais cela présente le désavantage que les expressions ne sont alors plus homogènes, alors que cette homogénéité peut permettre de repérer ses erreurs de calcul). Si par après on considère un point $P$ quelconque sur $[AC]$, on pourra paramétrer les coordonnées de $P$ par $(\lambda \cdot c_1, \lambda \cdot c_2)$ avec $\lambda \in [0,1]$.
A priori, une telle méthode peut sembler miraculeuse, puisqu'il semble toujours possible de calculer les coordonnées de tous les points de la figure ainsi que les équations de toutes les droites. En effet, calculer l'équation de la médiatrice d'un segment ou de la médiane d'un triangle n'est pas très compliqué. Malheureusement, cela devient vite moins gai lorsque l'on est amené à calculer l'équation d'une bissectrice ou pire : l'équation d'un cercle inscrit ou circonscrit à un triangle.
Bien que théoriquement, la géométrie analytique devrait permettre de résoudre tous les problèmes existants, c'est en pratique rarement le cas. Il existe cependant certaines situations plus favorables à une solution analytique. C'est le cas lorsque la figure consiste principalement en des milieux, des perpendiculaires ou des simples droites reliant deux sommets. Dans une telle configuration, l'étudiant ne parvenant pas à fournir une solution classique ne doit donc pas hésiter à tenter la voie analytique, tout en gardant à l'esprit qu'elle peut ne pas aboutir car demande des calculs trop lourds.
Si on parvient à trouver les équations ou les coordonnées des objets sur lesquels portent la thèse, alors il reste encore à vérifier cette dernière. Si les expressions que l'on a obtenues ne sont pas trop compliquées, on peut généralement s'en sortir, mais il se peut aussi que la conclusion doive passer par la résolution d'une équation de très haut degré, auquel cas il n'est pas impossible que la solution analytique ne puisse pas terminer le problème.
Bien sûr, il y a souvent des libertés dans la figure et il faudra alors faire usage de paramètres pour procéder de cette façon. Si on est en présence d'un triangle $ABC$, on peut par exemple poser l'origine du repère en $A$ et pointer l'axe des abscisses vers $B$. De la sorte, les coordonnées de $A$ sont $(0,0)$, les coordonnées de $B$ sont $(b,0)$ pour un certain $b > 0$, et les coordonnées de $C$ sont $(c_1,c_2)$ pour certains $c_1, c_2$. On peut éventuellement se simplifier la vie en posant $|AB| = 1$, de sorte que $b = 1$ (mais cela présente le désavantage que les expressions ne sont alors plus homogènes, alors que cette homogénéité peut permettre de repérer ses erreurs de calcul). Si par après on considère un point $P$ quelconque sur $[AC]$, on pourra paramétrer les coordonnées de $P$ par $(\lambda \cdot c_1, \lambda \cdot c_2)$ avec $\lambda \in [0,1]$.
A priori, une telle méthode peut sembler miraculeuse, puisqu'il semble toujours possible de calculer les coordonnées de tous les points de la figure ainsi que les équations de toutes les droites. En effet, calculer l'équation de la médiatrice d'un segment ou de la médiane d'un triangle n'est pas très compliqué. Malheureusement, cela devient vite moins gai lorsque l'on est amené à calculer l'équation d'une bissectrice ou pire : l'équation d'un cercle inscrit ou circonscrit à un triangle.
Bien que théoriquement, la géométrie analytique devrait permettre de résoudre tous les problèmes existants, c'est en pratique rarement le cas. Il existe cependant certaines situations plus favorables à une solution analytique. C'est le cas lorsque la figure consiste principalement en des milieux, des perpendiculaires ou des simples droites reliant deux sommets. Dans une telle configuration, l'étudiant ne parvenant pas à fournir une solution classique ne doit donc pas hésiter à tenter la voie analytique, tout en gardant à l'esprit qu'elle peut ne pas aboutir car demande des calculs trop lourds.
Si on parvient à trouver les équations ou les coordonnées des objets sur lesquels portent la thèse, alors il reste encore à vérifier cette dernière. Si les expressions que l'on a obtenues ne sont pas trop compliquées, on peut généralement s'en sortir, mais il se peut aussi que la conclusion doive passer par la résolution d'une équation de très haut degré, auquel cas il n'est pas impossible que la solution analytique ne puisse pas terminer le problème.
Formules utiles
Étant donnée une droite du plan orthonormé, on dira que sa pente est $(v_1,v_2)$ si, lorsqu'on se déplace de $v_1$ vers la droite, on se déplace de $v_2$ vers le haut. Typiquement, si la droite passe par les deux points $A \ (a_1, a_2)$ et $B \ (b_1, b_2)$, alors sa pente est $(b_1 - a_1, b_2 - a_2)$. À noter que la pente n'est pas unique : si une droite est de pente $(v_1, v_2)$ alors on peut aussi dire qu'elle est de pente $(\lambda \cdot v_1, \lambda \cdot v_2)$ pour tout $\lambda \neq 0$.- Équation de la droite de pente $(v_1, v_2)$ et passant par le point $(a_1, a_2)$ : l'idée est que si $(x,y)$ est un point de la droite, alors la pente calculée à partir de $(a_1,a_2)$ et $(x,y)$ doit être exactement $(v_1,v_2)$ (ou un multiple). L'équation de la droite est donc $\frac{x-a_1}{v_1} = \frac{y-a_2}{v_2}$. Notons cependant que cette formule n'est pas valable lorsque $v_1$ ou $v_2$ est nul. Pour avoir une formule qui est toujours valable, il suffit de réduire au même dénominateur pour obtenir $v_2(x-a_1) = v_1(y-a_2)$. Il est toutefois plus simple de retenir la première formule (puisqu'elle est intuitivement logique) et d'en déduire la deuxième.
- Équation d'une droite passant par $(a_1, a_2)$ et $(b_1, b_2)$ : sa pente est alors $(b_1-a_1, b_2-a_2)$ et on a donc par la formule précédente que son équation est $\frac{x-a_1}{b_1-a_1} = \frac{y-a_2}{b_2-a_2}$. Même remarque qu'au point précédent si $a_1 = b_1$ ou $a_2 = b_2$.
- Pente d'une droite perpendiculaire à une droite de pente $(v_1,v_2)$ : si on a une droite $d$ de pente $(v_1,v_2)$ et une droite $d'$ perpendiculaire à $d$, alors la pente de $d'$ est toujours $(v_2, -v_1)$ (ou $(-v_2, v_1)$, ce qui est pareil). On peut s'en convaincre par un dessin, ou en utilisant le produit scalaire pour ceux qui connaissent.
- Pente d'une droite parallèle à une droite de pente $(v_1, v_2)$ : forcément, si deux droites sont parallèles alors elles ont la même pente.
- Coordonnées du milieu de $A \ (a_1, a_2)$ et $B \ (b_1, b_2)$ : il suffit de faire la moyenne arithmétique des coordonnées : $M \ (\frac{a_1+b_1}{2}, \frac{a_2+b_2}{2})$.
- Coordonnées du centre de gravité du triangle de sommets $A \ (a_1, a_2)$, $B \ (b_1, b_2)$ et $C \ (c_1, c_2)$ : là aussi il s'agit de la moyenne arithmétique des coordonnées : $G \ (\frac{a_1+b_1+c_1}{3}, \frac{a_2+b_2+c_2}{3})$.
- Distance entre deux points $A \ (a_1, a_2)$ et $B \ (b_1, b_2)$ : il s'agit juste d'une application du théorème de Pythagore, et on trouve $|AB| = \sqrt{(b_1-a_1)^2 + (b_2-a_2)^2}$
- Équation du cercle de centre $O \ (o_1, o_2)$ et de rayon $r$ : il s'agit de l'ensemble des points à distance $r$ de $O$, donc son équation est $(x-o_1)^2 + (y-o_2)^2 = r^2$ (cela découle du point 7).
2. BxMO 2014
Voici le problème 4 de la BxMO (Benelux Mathematical Olympiad) 2014 :
Lors de la compétition, aucun participant n'a résolu ce problème. Celui-ci n'était pourtant pas insurmontable, et ces mauvais résultats sont certainement dus au manque de temps (puisqu'il y avait trois autres problèmes à résoudre en même temps). Ce problème possède bien sûr une solution classique (et c'est un bon exercice de la chercher), mais il était en fait également possible de le résoudre par géométrie analytique. La présence d'un carré et l'absence de cercles (qui compliquent souvent tout) est en effet un bon indicateur du fait qu'il devrait être possible d'utiliser la géométrie analytique.
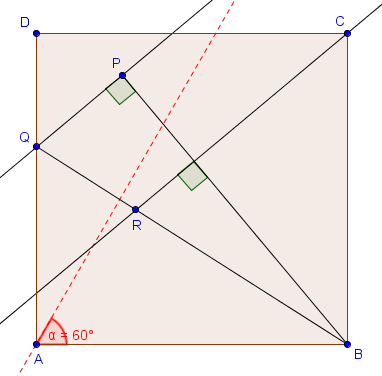
Problème (BxMO 2014, P4)
Soit $ABCD$ un carré. On considère un point variable $P$ à l’intérieur du carré tel que $\widehat{BAP} ≥ 60^\circ$. Soit $Q$ l’intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. Soit $R$ l’intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$.
(a) Prouver que $|BP| \geq |BR|$.
(b) Pour quel(s) point(s) $P$ l’inégalité en (a) devient-elle une égalité ?
(a) Prouver que $|BP| \geq |BR|$.
(b) Pour quel(s) point(s) $P$ l’inégalité en (a) devient-elle une égalité ?
Lors de la compétition, aucun participant n'a résolu ce problème. Celui-ci n'était pourtant pas insurmontable, et ces mauvais résultats sont certainement dus au manque de temps (puisqu'il y avait trois autres problèmes à résoudre en même temps). Ce problème possède bien sûr une solution classique (et c'est un bon exercice de la chercher), mais il était en fait également possible de le résoudre par géométrie analytique. La présence d'un carré et l'absence de cercles (qui compliquent souvent tout) est en effet un bon indicateur du fait qu'il devrait être possible d'utiliser la géométrie analytique.

Solution analytique
Naturellement, posons l'origine de notre repère comme étant $A$, l'axe des abscisses pointant vers $B$ et l'axe des ordonnées vers $D$. On peut aussi supposer que le carré est de côté $1$. On a alors $\boxed{A \ (0,0)}$, $\boxed{B \ (1, 0)}$, $\boxed{C \ (1,1)}$ et $\boxed{D \ (0,1)}$.
Notons ensuite $\boxed{P \ (p_1,p_2)}$ avec $0 < p_1, p_2 < 1$. Essayons de traduire $\widehat{BAP} \geq 60^\circ$ en équations. La droite passant par $A$ et faisant un angle de $60^\circ$ avec $AB$ a pour équation $y = \sqrt{3} \cdot x$ (comme on peut s'en convaincre de différentes façons), et $P$ doit se situer au dessus de cette droite, donc on a $\boxed{p_2 \geq \sqrt{3} \cdot p_1}$.
Le point $Q$ est maintenant l'intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. La pente de la droite $BP$ est $(p_1-1, p_2)$, et donc la pente d'une perpendiculaire à $BP$ est $(p_2, 1-p_1)$ (voir formules dans le point théorique précédent). L'équation de la droite de pente $(p_2, 1-p_1)$ passant par $P \ (p_1, p_2)$ est alors
$$\frac{x-p_1}{p_2} = \frac{y-p_2}{1-p_1}. \quad (1)$$ Nous cherchons l'intersection de cette droite avec la droite $AD$, qui a la simple équation $x = 0$. Il suffit donc de poser $x = 0$ dans $(1)$ et de trouver $y$. On obtient $y = p_2 + \frac{(p_1-1)p_1}{p_2} = \frac{p_2^2 + p_1^2 - p_1}{p_2}$. Donc les coordonnées de $Q$ sont $\boxed{Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)}$.
Le point $R$ est l'intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$. Nous avons déjà dit qu'une perpendiculaire à $BP$ avait pour pente $(p_2, 1-p_1)$, et la perpendiculaire à $BP$ passant par $C \ (1,1)$ a donc pour équation :
$$\frac{x-1}{p_2} = \frac{y-1}{1-p_1}$$ $$\Leftrightarrow (1-p_1)(x-1) = p_2(y-1). \quad (2)$$ D'autre part, la droite $BQ$ passe par $B \ (1,0)$ et $Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$, donc sa pente est $\left(-1, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$ et son équation est
$$\frac{x-1}{-1} = \frac{y-0}{\frac{p_2^2 + p_1^2 - p_1}{p_2}}. \quad (3)$$ Il reste à remettre $(2)$ et $(3)$ ensemble pour trouver les coordonnées de $R$. Par $(3)$, on voit que $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x)$. En remplaçant $y$ par cette expression dans $(2)$, on trouve alors que
$$(1-p_1)(x-1) = p_2\left(\frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) - 1\right)$$ $$\Leftrightarrow (1-p_1)x + p_1 - 1 = p_2^2+p_1^2-p_1-p_2 - (p_2^2+p_1^2-p_1)\cdot x$$ $$\Leftrightarrow (p_2^2+p_1^2-2p_1+1)\cdot x = p_2^2-p_2+p_1^2-2p_1+1$$ $$\Leftrightarrow (p_2^2 + (p_1-1)^2)\cdot x = p_2^2-p_2+ (p_1-1)^2$$ $$\Leftrightarrow x = \frac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}$$ On peut alors trouver $1-x = \frac{p_2}{p_2^2 + (p_1-1)^2}$ et donc $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) = \frac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2}$. Les coordonnées de $R$ sont donc $\boxed{R \ \left( \dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}, \ \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2 + (p_1-1)^2} \right)}$, et heureusement il n'y a plus de coordonnées à calculer...
Nous cherchons à montrer que $|BP| \geq |BR|$, ce qui revient à dire que $|BP|^2 \geq |BR|^2$. D'une part, on a $|BP|^2 = (p_1-1)^2 + p_2^2$, et d'autre part, on a
$$\begin{align}
|BR|^2 &= \left(\dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2} - 1\right)^2 + \left( \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2} \right)^2\\
&= \left(\dfrac{-p_2}{p_2^2+ (p_1-1)^2}\right)^2 + \left( 1+\dfrac{p_1-1}{p_2^2 + (p_1-1)^2} \right)^2\\
&= \frac{p_2^2}{(p_2^2+ (p_1-1)^2)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} + \frac{(p_1-1)^2}{(p_2^2+ (p_1-1)^2)^2}\\
&= \frac{1}{p_2^2+ (p_1-1)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} \\
&= \frac{2p_1-1+p_2^2+(p_1-1)^2}{p_2^2+ (p_1-1)^2} \\
&= \frac{p_2^2+p_1^2}{p_2^2+ (p_1-1)^2}
\end{align}$$ L'inégalité $|BP|^2 \geq |BR|^2$ se réécrit donc
$$(p_2^2+(p_1-1)^2)^2 \geq p_2^2+p_1^2, \quad (4)$$ dont on remarque qu'il s'agit juste de
$$|BP|^2 \geq |AP|.$$ Il serait possible de continuer avec $p_1$ et $p_2$ et de montrer que l'inégalité est vraie en utilisant que $p_2 \geq \sqrt{3} \cdot p_1$, mais il est en fait plus facile d'essayer de prouver que $|BP|^2 \geq |AP|$ plus géométriquement. En effet, on sait par la loi des cosinus dans le triangle $ABP$ que $|BP|^2 = |AB|^2+|AP|^2 - 2|AB||AP|\cos\widehat{BAP} = 1 + |AP|^2 - 2 |AP|\cos \widehat{BAP}$, et l'inégalité $|BP|^2 \geq |AP|$ peut donc se réécrire comme
$$1 + |AP|^2 - 2 |AP| \cos \widehat{BAP} \geq |AP|$$ $$\Leftrightarrow |AP|^2 - (2 \cos \widehat{BAP}+1) \cdot |AP| + 1 \geq 0.$$ Il s'agit d'une équation du second degré en $|AP|$, dont le discriminant est $(2 \cos \widehat{BAP}+1)^2 - 4$. Comme $60^\circ \leq \widehat{BAP} < 90^\circ$, on a $0 < \cos \widehat{BAP} \leq \frac 12$ et le discriminant est toujours négatif ou nul. Puisque le coefficient de $|AP|^2$ est positif, on en déduit que ce polynôme est toujours positif et nous avons donc prouvé (a). La seule façon d'avoir l'égalité est que le discriminant soit nul, i.e. que $\widehat{BAP} = 60^\circ$, et que $|AP|$ soit l'unique racine du polynôme, qui est alors $|AP| = 1$. Le point $P$ satisfaisant ces deux conditions est le point à l'intérieur de $ABCD$ tel que $ABP$ est équilatéral, ce qui répond au point (b).
Notons ensuite $\boxed{P \ (p_1,p_2)}$ avec $0 < p_1, p_2 < 1$. Essayons de traduire $\widehat{BAP} \geq 60^\circ$ en équations. La droite passant par $A$ et faisant un angle de $60^\circ$ avec $AB$ a pour équation $y = \sqrt{3} \cdot x$ (comme on peut s'en convaincre de différentes façons), et $P$ doit se situer au dessus de cette droite, donc on a $\boxed{p_2 \geq \sqrt{3} \cdot p_1}$.
Le point $Q$ est maintenant l'intersection de la droite $AD$ avec la perpendiculaire à $BP$ en $P$. La pente de la droite $BP$ est $(p_1-1, p_2)$, et donc la pente d'une perpendiculaire à $BP$ est $(p_2, 1-p_1)$ (voir formules dans le point théorique précédent). L'équation de la droite de pente $(p_2, 1-p_1)$ passant par $P \ (p_1, p_2)$ est alors
$$\frac{x-p_1}{p_2} = \frac{y-p_2}{1-p_1}. \quad (1)$$ Nous cherchons l'intersection de cette droite avec la droite $AD$, qui a la simple équation $x = 0$. Il suffit donc de poser $x = 0$ dans $(1)$ et de trouver $y$. On obtient $y = p_2 + \frac{(p_1-1)p_1}{p_2} = \frac{p_2^2 + p_1^2 - p_1}{p_2}$. Donc les coordonnées de $Q$ sont $\boxed{Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)}$.
Le point $R$ est l'intersection de la droite $BQ$ avec la perpendiculaire à $BP$ passant par $C$. Nous avons déjà dit qu'une perpendiculaire à $BP$ avait pour pente $(p_2, 1-p_1)$, et la perpendiculaire à $BP$ passant par $C \ (1,1)$ a donc pour équation :
$$\frac{x-1}{p_2} = \frac{y-1}{1-p_1}$$ $$\Leftrightarrow (1-p_1)(x-1) = p_2(y-1). \quad (2)$$ D'autre part, la droite $BQ$ passe par $B \ (1,0)$ et $Q \left(0, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$, donc sa pente est $\left(-1, \dfrac{p_2^2 + p_1^2 - p_1}{p_2}\right)$ et son équation est
$$\frac{x-1}{-1} = \frac{y-0}{\frac{p_2^2 + p_1^2 - p_1}{p_2}}. \quad (3)$$ Il reste à remettre $(2)$ et $(3)$ ensemble pour trouver les coordonnées de $R$. Par $(3)$, on voit que $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x)$. En remplaçant $y$ par cette expression dans $(2)$, on trouve alors que
$$(1-p_1)(x-1) = p_2\left(\frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) - 1\right)$$ $$\Leftrightarrow (1-p_1)x + p_1 - 1 = p_2^2+p_1^2-p_1-p_2 - (p_2^2+p_1^2-p_1)\cdot x$$ $$\Leftrightarrow (p_2^2+p_1^2-2p_1+1)\cdot x = p_2^2-p_2+p_1^2-2p_1+1$$ $$\Leftrightarrow (p_2^2 + (p_1-1)^2)\cdot x = p_2^2-p_2+ (p_1-1)^2$$ $$\Leftrightarrow x = \frac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}$$ On peut alors trouver $1-x = \frac{p_2}{p_2^2 + (p_1-1)^2}$ et donc $y = \frac{p_2^2 + p_1^2 - p_1}{p_2} \cdot (1-x) = \frac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2}$. Les coordonnées de $R$ sont donc $\boxed{R \ \left( \dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2}, \ \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2 + (p_1-1)^2} \right)}$, et heureusement il n'y a plus de coordonnées à calculer...
Nous cherchons à montrer que $|BP| \geq |BR|$, ce qui revient à dire que $|BP|^2 \geq |BR|^2$. D'une part, on a $|BP|^2 = (p_1-1)^2 + p_2^2$, et d'autre part, on a
$$\begin{align}
|BR|^2 &= \left(\dfrac{p_2^2-p_2+ (p_1-1)^2}{p_2^2 + (p_1-1)^2} - 1\right)^2 + \left( \dfrac{p_2^2 + p_1^2 - p_1}{p_2^2+ (p_1-1)^2} \right)^2\\
&= \left(\dfrac{-p_2}{p_2^2+ (p_1-1)^2}\right)^2 + \left( 1+\dfrac{p_1-1}{p_2^2 + (p_1-1)^2} \right)^2\\
&= \frac{p_2^2}{(p_2^2+ (p_1-1)^2)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} + \frac{(p_1-1)^2}{(p_2^2+ (p_1-1)^2)^2}\\
&= \frac{1}{p_2^2+ (p_1-1)^2} + 1 + \frac{2(p_1-1)}{p_2^2+ (p_1-1)^2} \\
&= \frac{2p_1-1+p_2^2+(p_1-1)^2}{p_2^2+ (p_1-1)^2} \\
&= \frac{p_2^2+p_1^2}{p_2^2+ (p_1-1)^2}
\end{align}$$ L'inégalité $|BP|^2 \geq |BR|^2$ se réécrit donc
$$(p_2^2+(p_1-1)^2)^2 \geq p_2^2+p_1^2, \quad (4)$$ dont on remarque qu'il s'agit juste de
$$|BP|^2 \geq |AP|.$$ Il serait possible de continuer avec $p_1$ et $p_2$ et de montrer que l'inégalité est vraie en utilisant que $p_2 \geq \sqrt{3} \cdot p_1$, mais il est en fait plus facile d'essayer de prouver que $|BP|^2 \geq |AP|$ plus géométriquement. En effet, on sait par la loi des cosinus dans le triangle $ABP$ que $|BP|^2 = |AB|^2+|AP|^2 - 2|AB||AP|\cos\widehat{BAP} = 1 + |AP|^2 - 2 |AP|\cos \widehat{BAP}$, et l'inégalité $|BP|^2 \geq |AP|$ peut donc se réécrire comme
$$1 + |AP|^2 - 2 |AP| \cos \widehat{BAP} \geq |AP|$$ $$\Leftrightarrow |AP|^2 - (2 \cos \widehat{BAP}+1) \cdot |AP| + 1 \geq 0.$$ Il s'agit d'une équation du second degré en $|AP|$, dont le discriminant est $(2 \cos \widehat{BAP}+1)^2 - 4$. Comme $60^\circ \leq \widehat{BAP} < 90^\circ$, on a $0 < \cos \widehat{BAP} \leq \frac 12$ et le discriminant est toujours négatif ou nul. Puisque le coefficient de $|AP|^2$ est positif, on en déduit que ce polynôme est toujours positif et nous avons donc prouvé (a). La seule façon d'avoir l'égalité est que le discriminant soit nul, i.e. que $\widehat{BAP} = 60^\circ$, et que $|AP|$ soit l'unique racine du polynôme, qui est alors $|AP| = 1$. Le point $P$ satisfaisant ces deux conditions est le point à l'intérieur de $ABCD$ tel que $ABP$ est équilatéral, ce qui répond au point (b).
Remarque importante
On voit sur cet exemple que les calculs deviennent vite laborieux en géométrie analytique. La moindre erreur dans le calcul d'une coordonnée est d'ailleurs fatale, et il faut donc être très concentré pour envisager un tel développement. Puisque ce genre de solution peut vite prendre beaucoup de temps, il est primordial en compétition de ne pas se lancer dans des solutions analytiques à tout bout de champ. Il serait dommage de passer tout son temps sur une telle solution en ignorant les autres problèmes, d'autant plus qu'elle peut ne pas aboutir. Il faut aussi noter que les solutions analytiques sont souvent mal payées en points lors de compétitions. Si une solution complète au problème est donnée, comme ci-dessus, alors elle sera gratifiée d'un score de $7/7$, mais si on arrive par exemple à l'inégalité $(4)$ sans parvenir à conclure alors on n'obtiendra que très peu de points (pas plus de $2/7$, et cela peut être encore plus sévère).
3. Trigonométrie
Lorsqu'une égalité de longueurs doit être démontrée, il peut être tentant de se lancer dans une résolution trigonométrique du problème. L'idée est généralement de commencer par noter $\alpha$, $\beta$, $\gamma$,... les différents angles de la figure (tout en essayant d'utiliser le moins de lettres possibles : une solution trigonométrique doit avant tout commencer par une chasse aux angles permettant de déterminer les relations élémentaires entre les différents angles et d'ainsi garder le moins d'inconnues possible). On essaye alors d'utiliser la trigonométrie, généralement la loi des sinus, pour obtenir des relations entre les différentes longueurs de segments. L'objectif est généralement de parvenir à réexprimer la thèse initiale en une nouvelle thèse purement trigonométrique. On peut alors typiquement arriver à une conclusion du type "Pour terminer le problème, je dois prouver que
$$\sin(\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$$ pour $\alpha$ et $\beta$ inconnus". Évidemment, obtenir une équation si simple serait une aubaine : les équations auxquelles on arrive en général peuvent être beaucoup plus compliquées. De bonnes connaissances des formules de trigonométrie pourront alors aider l'étudiant à tenter de démontrer l'équation obtenue, mais il faut là aussi garder à l'esprit qu'il n'est peut-être pas possible de le faire aisément.
Même s'il est rare que la trigonométrie permette de résoudre entièrement un problème, il est plus fréquent qu'un peu de trigonométrie soit utile à la résolution du problème. Parfois, des raisonnements classiques permettent de simplifier le problème, et il est plus facile de résoudre le problème ainsi simplifié par trigonométrie plutôt que par un nouveau raisonnement classique. Il ne faut donc pas perdre de vue cette méthode qui se révèle parfois payante, quoique là aussi peu élégante.
$$\sin(\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$$ pour $\alpha$ et $\beta$ inconnus". Évidemment, obtenir une équation si simple serait une aubaine : les équations auxquelles on arrive en général peuvent être beaucoup plus compliquées. De bonnes connaissances des formules de trigonométrie pourront alors aider l'étudiant à tenter de démontrer l'équation obtenue, mais il faut là aussi garder à l'esprit qu'il n'est peut-être pas possible de le faire aisément.
Même s'il est rare que la trigonométrie permette de résoudre entièrement un problème, il est plus fréquent qu'un peu de trigonométrie soit utile à la résolution du problème. Parfois, des raisonnements classiques permettent de simplifier le problème, et il est plus facile de résoudre le problème ainsi simplifié par trigonométrie plutôt que par un nouveau raisonnement classique. Il ne faut donc pas perdre de vue cette méthode qui se révèle parfois payante, quoique là aussi peu élégante.
Formules utiles
- Pour envisager la trigonométrie dans la résolution d'un problème, il est bien sûr primordial de maîtriser la manipulation des fonctions trigonométriques. Il faut aussi connaître toutes les formules impliquant ces fonctions. Toutes ces bases sont rappelées sur ce site dans le chapitre sur la trigonométrie.
- La formule la plus utilisée dans une preuve par trigonométrie est la loi des sinus.
4. IMO 2009
Voici le problème 4 de l'IMO 2009 :
Encore une fois, ce problème possède une solution "classique", mais la plupart des participants à l'IMO cette année-là l'ont en fait résolu avec de la trigonométrie. Il n'est toutefois pas évident de savoir par où commencer, et il faut à tout prix éviter de tourner en rond.
Problème (IMO 2009, P4)
Soit $ABC$ un triangle tel que $|AB| = |AC|$. Les bissectrices de $\widehat{CAB}$ et $\widehat{ABC}$ rencontrent respectivement les côtés $[BC]$ et $[CA]$ en $D$ et $E$. Soit $K$ le centre du cercle inscrit dans le triangle $ADC$. On suppose que $\widehat{BEK} = 45^\circ$. Trouver toutes les valeurs possibles de $\widehat{CAB}$.
Encore une fois, ce problème possède une solution "classique", mais la plupart des participants à l'IMO cette année-là l'ont en fait résolu avec de la trigonométrie. Il n'est toutefois pas évident de savoir par où commencer, et il faut à tout prix éviter de tourner en rond.
Solution trigonométrique
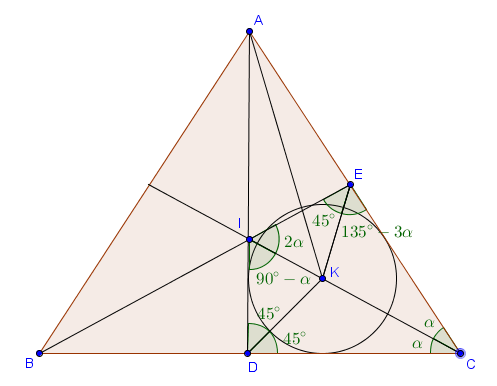
Notons $I$ l'intersection des bissectrices de $ABC$. Les points $C$, $K$ et $I$ sont alignés. Posons également $\alpha = \widehat{ICD}$. Nous allons appliquer la loi des sinus dans les triangles $DIK$, $KIE$, $EKC$ et $CKD$. Pour cela, il faut exprimer tous les angles intervenant dans ces triangles en fonction de $\alpha$.
Appliquons maintenant nos lois des sinus :
$$\sin(90^\circ-\alpha)\cdot \sin 45^\circ\cdot \sin \alpha\cdot \sin 45^\circ = \sin 45^\circ\cdot \sin 2\alpha\cdot \sin(135^\circ-3\alpha)\cdot \sin \alpha,$$ ce qui se réécrit encore en utilisant que $\sin(90^\circ - \alpha) = \cos \alpha$ et que $\sin2\alpha = 2 \sin \alpha \cos \alpha$ :
$$\sin 45^\circ = 2 \sin \alpha \cdot \sin(135^\circ-3\alpha).$$ Puisque $\sin(135^\circ - 3\alpha) = \sin(45^\circ + 3\alpha) = \sin 45^\circ \cdot \cos 3\alpha + \cos 45^\circ \cdot \sin 3\alpha = \sin 45^\circ \cdot (\cos 3\alpha + \sin 3\alpha)$, l'équation se réécrit encore
$$1 = 2\sin \alpha \cdot (\cos 3 \alpha + \sin 3 \alpha).$$ Il nous reste à résoudre cette équation trigonométrique en $\alpha$. Il y a plusieurs façons de procéder, voici une manière.
On peut développer $\cos 3\alpha = \cos (2\alpha+\alpha)$ et $\sin 3 \alpha = \sin(2\alpha+\alpha)$. L'équation devient
$$\begin{align}
1 &= 2 \sin \alpha \cdot (\cos 2\alpha \cos \alpha - \sin 2\alpha \sin \alpha + \sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha)\\
&= 2 \sin \alpha \cdot \cos \alpha \cdot (\cos 2\alpha + \sin 2\alpha) + 2\sin^2 \alpha \cdot (\cos 2\alpha - \sin 2\alpha)\\
\end{align}$$ Or, on a $2 \sin \alpha \cos \alpha = \sin 2\alpha$ et $2 \sin^2\alpha = 1 - \cos 2 \alpha$, donc
$$\begin{align}
&1 = \sin 2\alpha \cdot (\cos 2\alpha + \sin 2\alpha) + (1 - \cos 2\alpha) \cdot (\cos 2\alpha - \sin 2\alpha)\\
\Leftrightarrow \ & 1 = 2 \sin 2\alpha \cos 2\alpha + \sin^2 2\alpha - \cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = 2 \sin 2\alpha \cos 2\alpha - 2\cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = (2 \cos 2 \alpha - 1)(\sin 2\alpha - \cos 2\alpha)
\end{align}$$ On en déduit que $\alpha$ doit respecter $\cos 2\alpha = \frac{1}{2}$ ou $\cos 2\alpha = \sin 2\alpha$ pour pouvoir respecter les conditions de l'énoncé. La première équation donne $2\alpha = 60^\circ$ et la deuxième donne $2\alpha = 45^\circ$. Puisque $\widehat{BAC} = 180^\circ-4\alpha$, cet angle doit valoir $60^\circ$ ou $90^\circ$. Il est important de noter que, tout comme pour une équation fonctionnelle, il faut ici vérifier que ces deux angles $60^\circ$ et $90^\circ$ donnent bien lieu à $\widehat{BEK} = 45^\circ$. Nous ne nous étendons pas sur ce point car c'est un simple exercice, mais les distraits ayant oublié cette vérification en 2009 se sont vu attribuer un score de $5/7$ pour cette question.
- $\widehat{KCE} = \alpha$
- $\widehat{KCD} = \alpha$
- $\widehat{KDC} = 45^\circ$
- $\widehat{KDI} = 45^\circ$
- $\widehat{KID} = \widehat{CID} = 90^\circ - \widehat{ICD} = 90^\circ - \alpha$
- $\widehat{KIE} = 180^\circ - \widehat{BID} - \widehat{DIK} = 180^\circ - (90^\circ-\alpha) - (90^\circ-\alpha) = 2\alpha$
- $\widehat{KEI} = 45^\circ$ (par hypothèse)
- $\widehat{KEC} = \widehat{BEC} - \widehat{BEK} = 180^\circ - 3\alpha - 45^\circ = 135^\circ - 3\alpha$

Appliquons maintenant nos lois des sinus :
- Dans le triangle $DIK$, on obtient
$$\frac{|IK|}{\sin 45^\circ} = \frac{|DK|}{\sin(90^\circ - \alpha)}$$ - Dans le triangle $KIE$, on obtient
$$\frac{|EK|}{\sin 2\alpha} = \frac{|IK|}{\sin 45^\circ}$$ - Dans le triangle $EKC$, on obtient
$$\frac{|CK|}{\sin(135^\circ-3\alpha)} = \frac{|EK|}{\sin \alpha}$$ - Dans le triangle $CKD$, on obtient
$$\frac{|DK|}{\sin\alpha} = \frac{|CK|}{\sin 45^\circ}$$
$$\sin(90^\circ-\alpha)\cdot \sin 45^\circ\cdot \sin \alpha\cdot \sin 45^\circ = \sin 45^\circ\cdot \sin 2\alpha\cdot \sin(135^\circ-3\alpha)\cdot \sin \alpha,$$ ce qui se réécrit encore en utilisant que $\sin(90^\circ - \alpha) = \cos \alpha$ et que $\sin2\alpha = 2 \sin \alpha \cos \alpha$ :
$$\sin 45^\circ = 2 \sin \alpha \cdot \sin(135^\circ-3\alpha).$$ Puisque $\sin(135^\circ - 3\alpha) = \sin(45^\circ + 3\alpha) = \sin 45^\circ \cdot \cos 3\alpha + \cos 45^\circ \cdot \sin 3\alpha = \sin 45^\circ \cdot (\cos 3\alpha + \sin 3\alpha)$, l'équation se réécrit encore
$$1 = 2\sin \alpha \cdot (\cos 3 \alpha + \sin 3 \alpha).$$ Il nous reste à résoudre cette équation trigonométrique en $\alpha$. Il y a plusieurs façons de procéder, voici une manière.
On peut développer $\cos 3\alpha = \cos (2\alpha+\alpha)$ et $\sin 3 \alpha = \sin(2\alpha+\alpha)$. L'équation devient
$$\begin{align}
1 &= 2 \sin \alpha \cdot (\cos 2\alpha \cos \alpha - \sin 2\alpha \sin \alpha + \sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha)\\
&= 2 \sin \alpha \cdot \cos \alpha \cdot (\cos 2\alpha + \sin 2\alpha) + 2\sin^2 \alpha \cdot (\cos 2\alpha - \sin 2\alpha)\\
\end{align}$$ Or, on a $2 \sin \alpha \cos \alpha = \sin 2\alpha$ et $2 \sin^2\alpha = 1 - \cos 2 \alpha$, donc
$$\begin{align}
&1 = \sin 2\alpha \cdot (\cos 2\alpha + \sin 2\alpha) + (1 - \cos 2\alpha) \cdot (\cos 2\alpha - \sin 2\alpha)\\
\Leftrightarrow \ & 1 = 2 \sin 2\alpha \cos 2\alpha + \sin^2 2\alpha - \cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = 2 \sin 2\alpha \cos 2\alpha - 2\cos^2 2\alpha + \cos 2\alpha - \sin 2\alpha\\
\Leftrightarrow \ & 0 = (2 \cos 2 \alpha - 1)(\sin 2\alpha - \cos 2\alpha)
\end{align}$$ On en déduit que $\alpha$ doit respecter $\cos 2\alpha = \frac{1}{2}$ ou $\cos 2\alpha = \sin 2\alpha$ pour pouvoir respecter les conditions de l'énoncé. La première équation donne $2\alpha = 60^\circ$ et la deuxième donne $2\alpha = 45^\circ$. Puisque $\widehat{BAC} = 180^\circ-4\alpha$, cet angle doit valoir $60^\circ$ ou $90^\circ$. Il est important de noter que, tout comme pour une équation fonctionnelle, il faut ici vérifier que ces deux angles $60^\circ$ et $90^\circ$ donnent bien lieu à $\widehat{BEK} = 45^\circ$. Nous ne nous étendons pas sur ce point car c'est un simple exercice, mais les distraits ayant oublié cette vérification en 2009 se sont vu attribuer un score de $5/7$ pour cette question.