Théorie > Géométrie > Transformations du plan
Droite d'Euler
Dans un triangle $ABC$, les quatre points particuliers les plus fréquemment étudiés sont le centre du cercle circonscrit $O$, le centre du cercle inscrit $I$, l'orthocentre $H$ et le centre de gravité $G$. Il s'avère en fait que les points $O$, $H$ et $G$ sont toujours alignés, et la droite qu'ils forment s'appelle la droite d'Euler. (Si le triangle est équilatéral, les trois points sont confondus et il n'y a donc pas de droite d'Euler). Plus précisément, on a le résultat suivant. La démonstration de ce résultat est aussi intéressante que le résultat lui-même, car elle fait intervenir une homothétie et donne donc un autre exemple d'utilisation des transformations du plan.
Théorème (droite d'Euler)
Soit $ABC$ un triangle, $O$ son centre du cercle circonscrit, $H$ son orthocentre et $G$ son centre de gravité. Alors $H$, $G$ et $O$ sont alignés dans cet ordre (c'est-à-dire que $G \in [OH]$) et $|HG| = 2 \cdot |GO|$.
Démonstration
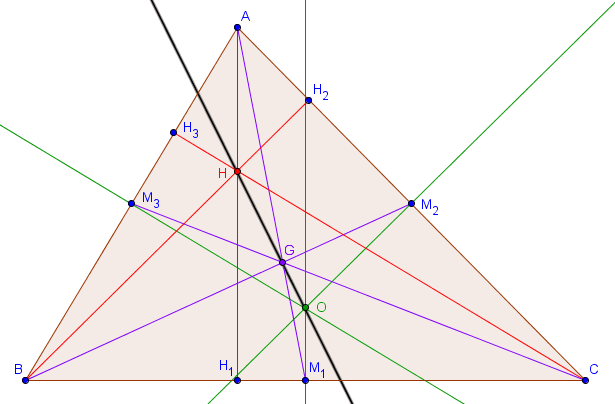
Sur le dessin ci-dessous, les points $M_1, M_2, M_3$ sont les milieux des trois côtés et les points $H_1, H_2, H_3$ sont les pieds des trois hauteurs.
Considérons l'homothétie $h$ de centre $G$ et de rapport $-\frac{1}{2}$. Puisque $G$ se trouve au tiers de chaque médiane, l'image de $A$ par $h$ est $M_1$, l'image de $B$ est $M_2$ et l'image de $C$ est $M_3$.
L'homothétie $h$ envoie donc la hauteur $AH_1$ sur une droite passant par $M_1$ et qui lui est parallèle. Comme $AH_1$ est perpendiculaire à $BC$, cette image doit donc également être perpendiculaire à $BC$ et il ne peut donc s'agir que de la médiatrice de $[BC]$. De la même manière, l'image par $h$ de $BH_2$ est la médiatrice de $[AC]$ et l'image de $CH_3$ est la médiatrice de $[AB]$. L'intersection $H$ des trois hauteurs est donc envoyée par $h$ sur l'intersection des trois médiatrices, à savoir $O$.
On en déduit directement que $H$, $G$ et $O$ sont alignés et que $|GO| = \frac{1}{2} \cdot |GH|$.
Considérons l'homothétie $h$ de centre $G$ et de rapport $-\frac{1}{2}$. Puisque $G$ se trouve au tiers de chaque médiane, l'image de $A$ par $h$ est $M_1$, l'image de $B$ est $M_2$ et l'image de $C$ est $M_3$.
L'homothétie $h$ envoie donc la hauteur $AH_1$ sur une droite passant par $M_1$ et qui lui est parallèle. Comme $AH_1$ est perpendiculaire à $BC$, cette image doit donc également être perpendiculaire à $BC$ et il ne peut donc s'agir que de la médiatrice de $[BC]$. De la même manière, l'image par $h$ de $BH_2$ est la médiatrice de $[AC]$ et l'image de $CH_3$ est la médiatrice de $[AB]$. L'intersection $H$ des trois hauteurs est donc envoyée par $h$ sur l'intersection des trois médiatrices, à savoir $O$.
On en déduit directement que $H$, $G$ et $O$ sont alignés et que $|GO| = \frac{1}{2} \cdot |GH|$.
