Théorie > Géométrie > Inversion et polarisation
Exemples d'application
Considérons le problème suivant.
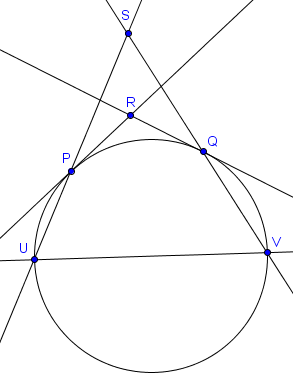
Voici un autre problème, un peu plus compliqué :
(Ces deux problèmes et leurs solutions proviennent de ce PDF. D'autres problèmes utilisant la polarisation s'y trouvent également et peuvent être consultés pour approfondir son entraînement.)
Problème
Soit $\mathcal{C}$ un cercle et $[UV]$ un de ses diamètres. On prend $P$ et $Q$ deux points sur $\mathcal{C}$, du même côté de $UV$ et avec $P$ plus proche de $U$ que $Q$. Les tangentes à $\mathcal{C}$ par $P$ et $Q$ s'intersectent en $R$. Si $S$ est le point d'intersection de $UP$ et $VQ$, alors montrer que $RS$ est perpendiculaire à $UV$.

Solution
Il s'agit typiquement du genre de problème où la polarisation pourrait être utile : il y a un cercle, des tangentes à ce cercle, et il faut démontrer qu'une droite ($RS$) est perpendiculaire à un certain diamètre ($UV$). En termes de polarisation, cette thèse signifie que $RS$ doit être la polaire par rapport à $\mathcal{C}$ d'un point appartenant à $UV$.
Il est donc naturel de considérer la polarisation par rapport à $\mathcal{C}$ et d'essayer de prouver que $RS$ est la polaire d'un point particulier de $UV$. Autrement dit, il suffit de prouver que le pôle de la droite $RS$ se situe sur $UV$. Nous savons déjà que la polaire de $R$ est exactement $PQ$ (voir point 3 dans les premières propriétés des polaires). Cela signifie que le pôle de $RS$ se situe sur $PQ$ (voir point 4). De plus, par le point 7, la polaire de $S$ est la droite $d$ passant par $PQ \cap UV$ et $PV \cap UQ$. À nouveau par le point 4 cela signifie que le pôle de $RS$ se situe sur cette droite $d$. De ces deux constatations, il découle que le pôle de $RS$ est le point d'intersection de $PQ$ et de $d$. Comme la droite $d$ passe par $PQ \cap UV$, l'intersection de ces deux droites est $PQ \cap UV$. On a donc bien démontré que le pôle de $RS$ se situe sur $UV$, ce qui implique que $RS$ est perpendiculaire à $UV$.
Notez que cet argument ne fonctionne pas quand $PQ$ est parallèle à $UV$ (car on ne peut alors pas appliquer le point 7). Cependant, si $PQ$ est parallèle à $UV$ alors la figure est complètement symétrique et il est évident que $RS$ est la médiatrice de $[UV]$.
Il est donc naturel de considérer la polarisation par rapport à $\mathcal{C}$ et d'essayer de prouver que $RS$ est la polaire d'un point particulier de $UV$. Autrement dit, il suffit de prouver que le pôle de la droite $RS$ se situe sur $UV$. Nous savons déjà que la polaire de $R$ est exactement $PQ$ (voir point 3 dans les premières propriétés des polaires). Cela signifie que le pôle de $RS$ se situe sur $PQ$ (voir point 4). De plus, par le point 7, la polaire de $S$ est la droite $d$ passant par $PQ \cap UV$ et $PV \cap UQ$. À nouveau par le point 4 cela signifie que le pôle de $RS$ se situe sur cette droite $d$. De ces deux constatations, il découle que le pôle de $RS$ est le point d'intersection de $PQ$ et de $d$. Comme la droite $d$ passe par $PQ \cap UV$, l'intersection de ces deux droites est $PQ \cap UV$. On a donc bien démontré que le pôle de $RS$ se situe sur $UV$, ce qui implique que $RS$ est perpendiculaire à $UV$.
Notez que cet argument ne fonctionne pas quand $PQ$ est parallèle à $UV$ (car on ne peut alors pas appliquer le point 7). Cependant, si $PQ$ est parallèle à $UV$ alors la figure est complètement symétrique et il est évident que $RS$ est la médiatrice de $[UV]$.
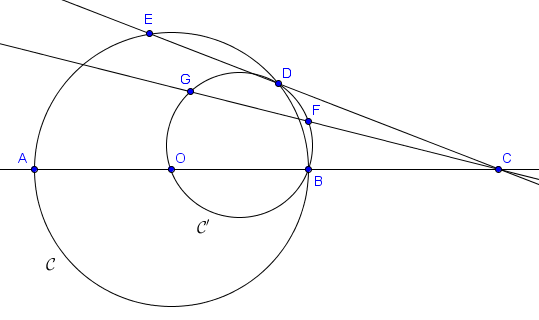
Voici un autre problème, un peu plus compliqué :
Problème (China Western Math Olympiad 2006)
Soit $\mathcal{C}$ un cercle de centre $O$, et $[AB]$ un diamètre de $\mathcal{C}$. Soit $C$ un point de $AB$ en dehors de $[AB]$, plus proche de $B$ que de $A$. Une droite passant par $C$ coupe $\mathcal{C}$ en $D$ et $E$. Le point $F$ est défini de sorte que $[OF]$ soit un diamètre du cercle circonscrit $\mathcal{C}'$ au triangle $BOD$. Enfin, la droite $CF$ intersecte $\mathcal{C}'$ à nouveau en $G$. Montrer que les points $O, A, E, G$ sont cocyliques.

Démonstration
La situation du point $C$ peut donner envie de s'intéresser à sa polaire par rapport à $\mathcal{C}$. Par le point 7, on sait que cette polaire est la droite passant par $P = AE \cap DB$ et $Q = EB \cap DA$. De la même manière, la polaire de $P$ est $CQ$. En particulier, $CQ$ est perpendiculaire à $OP$.
Notons $R$ l'intersection de ces deux droites perpendiculaires $CQ$ et $OP$. Sur le dessin ci-dessous, il semble que $R$ coïncide avec $G$ ! Si $R$ est effectivement égal à $G$, alors en particulier $G$ se situe sur $OP$ et on a successivement $|PE| \cdot |PA| = |PD| \cdot |PB| = |PG| \cdot |PO|$, ce qui implique que $AEGO$ est cyclique et termine le problème (on a ici utilisé les puissances de $P$ par rapport aux différents cercles). Il suffit donc pour conclure de prouver que $R = G$.
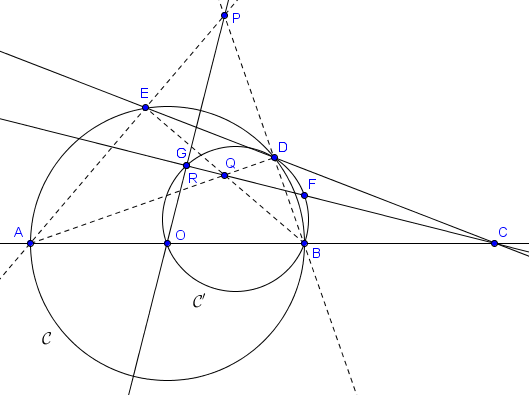
On a $\widehat{QRP} = 90^\circ = \widehat{QEP} = \widehat{QDP}$ (notez que $Q$ est l'orthocentre de $ABP$), donc les points $P, D, Q, R, E$ sont cocycliques. Donc $\widehat{DRP} = \widehat{DEP} = \widehat{ABP} = \widehat{OBD}$. Ainsi, le point $R$ se situe sur $\mathcal{C}'$. Mais on a aussi $\widehat{CRO} = 90^\circ$, donc $R$ se situe sur le cercle de diamètre $[CO]$. C'est aussi le cas de $G$ : il appartient à $\mathcal{C}'$ par définition et on a $\widehat{CGO} = \widehat{FGO} = 90^\circ$. Puisque le cercle de diamètre $[CO]$ n'intersecte $\mathcal{C'}$ qu'en un seul point différent de $O$, on en conclut que $R = G$.
Notons $R$ l'intersection de ces deux droites perpendiculaires $CQ$ et $OP$. Sur le dessin ci-dessous, il semble que $R$ coïncide avec $G$ ! Si $R$ est effectivement égal à $G$, alors en particulier $G$ se situe sur $OP$ et on a successivement $|PE| \cdot |PA| = |PD| \cdot |PB| = |PG| \cdot |PO|$, ce qui implique que $AEGO$ est cyclique et termine le problème (on a ici utilisé les puissances de $P$ par rapport aux différents cercles). Il suffit donc pour conclure de prouver que $R = G$.

On a $\widehat{QRP} = 90^\circ = \widehat{QEP} = \widehat{QDP}$ (notez que $Q$ est l'orthocentre de $ABP$), donc les points $P, D, Q, R, E$ sont cocycliques. Donc $\widehat{DRP} = \widehat{DEP} = \widehat{ABP} = \widehat{OBD}$. Ainsi, le point $R$ se situe sur $\mathcal{C}'$. Mais on a aussi $\widehat{CRO} = 90^\circ$, donc $R$ se situe sur le cercle de diamètre $[CO]$. C'est aussi le cas de $G$ : il appartient à $\mathcal{C}'$ par définition et on a $\widehat{CGO} = \widehat{FGO} = 90^\circ$. Puisque le cercle de diamètre $[CO]$ n'intersecte $\mathcal{C'}$ qu'en un seul point différent de $O$, on en conclut que $R = G$.
(Ces deux problèmes et leurs solutions proviennent de ce PDF. D'autres problèmes utilisant la polarisation s'y trouvent également et peuvent être consultés pour approfondir son entraînement.)