Concours > Concours #15

Description

Une nouvelle année, un nouveau concours ! Le format est similaire au concours précédent : $10$ problèmes aux sujets variés (et, qui sait, peut-être de la géométrie), en ordre croissant de difficulté (la plupart des problèmes restant assez accessibles), et des médailles à la fin.

On espère que chacun d'entre vous pourra profiter du concours, et y trouver des problèmes intéressants sur lesquels passer quelque temps.

Organisateurs du concours : Brique A., ¹³Corentin Bodart et ⁹Philémon Varnet.

• Problèmes
• Classement final
• Statistiques

Problème #1

Solutions acceptées du vendredi 15 janvier 2021 à 8h00 au dimanche 17 janvier 2021 à 18h00 (heures belges). Énoncé Soit $n> 1$ un naturel tel que $\varphi(n)$ divise $n-1$. Montrer que $n$ est squarefree, c'est-à-dire que le seul carré parfait divisant $n$ est $1$. Montrer que soit $n$ est premier, soit $n$ possède au moins $3$ facteurs premiers distincts. Bonus (ne rapportant pas de points) : Remplacer $3$ par $4$ dans le point 2. Statistiques Tenté par 51 personnes Scores parfaits : 40 Origine du problème : Problème de Lehmer

Problème #2

Solutions acceptées du vendredi 15 janvier 2021 à 8h00 au dimanche 17 janvier 2021 à 18h00 (heures belges). Énoncé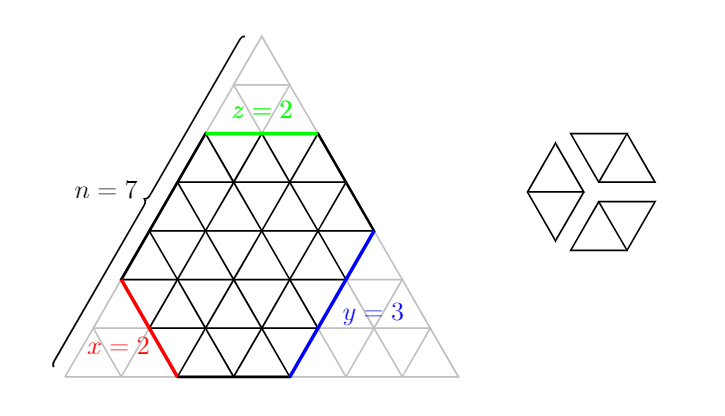 Déterminer l'ensemble des quadruplets $(n,x,y,z)\in\mathbb N^4$ vérifiant $n\ge \max\{x+y,y+z,z+x\}$ et tels que le domaine suivant (à gauche) est pavable avec une quantité suffisante des trois "dominos" de droite. Remarque : La condition $n\ge \max\{x+y,y+z,z+x\}$ est simplement là pour que le domaine soit bien défini. Statistiques Tenté par 23 personnes Scores parfaits : 14

Problème #3

Solutions acceptées du samedi 16 janvier 2021 à 8h00 au lundi 18 janvier 2021 à 18h00 (heures belges). Énoncé Soit $(F_n)_{n\ge 1}$ la suite de Fibonacci, définie par $F_1=F_2=1$ et $F_{n+2}=F_{n+1}+F_n$ pour tout $n\ge 1$. Montrer que, pour tout $n \ge 1$, on a $$\sqrt{F_{n}F_{n+3}} + \sqrt{F_{n+1}F_{n+4}} \le \sqrt{F_{n+2}F_{n+5}}.$$ Existe-t-il un $n \geq 1$ pour lequel cette inégalité est une égalité ? Statistiques Tenté par 36 personnes Scores parfaits : 25

Problème #4

Solutions acceptées du dimanche 17 janvier 2021 à 8h00 au mardi 19 janvier 2021 à 18h00 (heures belges). Énoncé Soit $ABC$ un triangle et $O$ le centre de son cercle circonscrit. Notons $A'$, $B'$, $C'$ les symétriques de $O$ par rapport aux milieux de $[BC]$, $[CA]$ et $[AB]$ respectivement. Montrer que les droites $AA'$, $BB'$ et $CC'$ sont concourantes. Statistiques Tenté par 28 personnes Scores parfaits : 27 Origine du problème : Abel Mathematics Competition, 2016-2017, Finale, Problème 2

Problème #5

Solutions acceptées du lundi 18 janvier 2021 à 8h00 au mercredi 20 janvier 2021 à 18h00 (heures belges). Énoncé Soient $a_1,a_2,\ldots,a_n$ des entiers formant une progression arithmétique (dans l'ordre). On suppose que $i$ divise $a_i$ pour $i\in\{1,2,\ldots,n-1\}$, mais que $n$ ne divise pas $a_n$. Montrer que $n$ est une puissance d'un nombre premier. Statistiques Tenté par 36 personnes Scores parfaits : 32

Problème #6

Solutions acceptées du mardi 19 janvier 2021 à 8h00 au jeudi 21 janvier 2021 à 18h00 (heures belges). Énoncé Tom joue à un solitaire sur une grille $n\times n$, initialement vide. Tour à tour, il remplit une case avec un $X$, compte le nombre de $X$ déjà présents sur la ligne et la colonne du nouveau $X$, et rajoute ce nombre à son total. Combien de points accumulera Tom une fois la grille remplie, au maximum ? Statistiques Tenté par 32 personnes Scores parfaits : 27 Origine du problème : Abel Mathematics Competition, 2018-2019, Finale, Problème 1

Problème #7

Solutions acceptées du mercredi 20 janvier 2021 à 8h00 au vendredi 22 janvier 2021 à 18h00 (heures belges). Énoncé Soit $ABC$ un triangle acutangle. Notons $D$ et $E$ les pieds des hauteurs issues de $B$ et $C$ respectivement, ainsi que $M$ le milieu de $[BC]$. La droite $AM$ intersecte les cercles circonscrits aux triangles $ADE$ et $ABC$ en $P$ et $Q$ respectivement. Montrer que $MP=MQ$. Statistiques Tenté par 23 personnes Scores parfaits : 16 Origine du problème : Estonia Team Selection Test 2014, Jour 2, Problème 1

Problème #8

Solutions acceptées du jeudi 21 janvier 2021 à 8h00 au samedi 23 janvier 2021 à 18h00 (heures belges). Énoncé Trouver toutes les fonctions $f\colon \mathbb R^+_0 \to \mathbb R^+_0$ telles que \[ f(x)f\big(yf(x)\big) = f(x + y) \ \text{ pour tous }x,y>0.\] Statistiques Tenté par 21 personnes Scores parfaits : 6

Problème #9

Solutions acceptées du vendredi 22 janvier 2021 à 8h00 au dimanche 24 janvier 2021 à 18h00 (heures belges). Énoncé Alice et Bob jouent à un jeu consistant à retirer alternativement des jetons d'une pile comptant initialement $2021$ jetons. Au premier tour, Alice retire un nombre non-nul de jetons, mais pas tous. Par la suite, chaque joueur peut prendre au plus le double du nombre de jetons retiré par l'adversaire au tour précédent. Le joueur prenant le dernier jeton gagne. Déterminer qui de Alice ou Bob possède une stratégie gagnante. Statistiques Tenté par 18 personnes Scores parfaits : 8 Origine du problème : Fibonacci Nim

Problème #10

Solutions acceptées du vendredi 22 janvier 2021 à 8h00 au dimanche 24 janvier 2021 à 18h00 (heures belges). Énoncé Soit $n \geq 2$ un entier. Un sous-ensemble $S$ de $\{0,1,..,n-1\}$ est dit $d$-couvrable s'il existe un polynôme $P$ à coefficients entiers et de degré au plus $d$ tel que $$S = \{ P(k)\pmod n \mid k \in \mathbb Z\}.$$ Pour chaque $n \geq 2$, trouver le plus petit $d$ tel que tout sous-ensemble non-vide de $\{0,1,..,n-1\}$ soit $d$-couvrable, ou prouver qu'aucun tel $d$ n'existe. Remarque : Des résultats partiels pour certaines familles infinies de $n$ pourront déjà être récompensés. Statistiques Tenté par 9 personnes Scores parfaits : 4 Origine du problème : ELMO Shortlist 2018, N4