Théorie > Géométrie > Cercles d'Apollonius
Droite de Lemoine
Nous avons vu comment obtenir un diamètre du $A$-cercle d'Apollonius : il suffit de prendre l'intersection de la bissectrice intérieure de $A$ avec $BC$ puis l'intersection de sa bissectrice extérieure avec $BC$. Le centre $O_A$ de ce cercle est donc pour le moment juste caractérisé comme étant le milieu de ce diamètre. En fait, ce centre peut être construit d'une autre manière : il se situe sur un des côtés du triangle tangentiel associé à $ABC$.
De la même façon, pourvu que $ABC$ n'est pas isocèle on peut construire le centre $O_B$ du $B$-cercle d'Apollonius et le centre $O_C$ du $C$-cercle d'Apollonius. Les trois centres sont alignés : cela découle du fait que les trois cercles ont exactement deux points communs. La droite de Lemoine est alors définie comme la droite passant par ces trois centres. Elle est représentée en rouge sur la figure suivante. Le cercle circonscrit au triangle $ABC$ ainsi que ses trois tangentes en $A$, $B$ et $C$ sont représenté en pointillés. Le triangle formé par ces trois tangentes est bien sûr le triangle tangentiel associé à $ABC$.
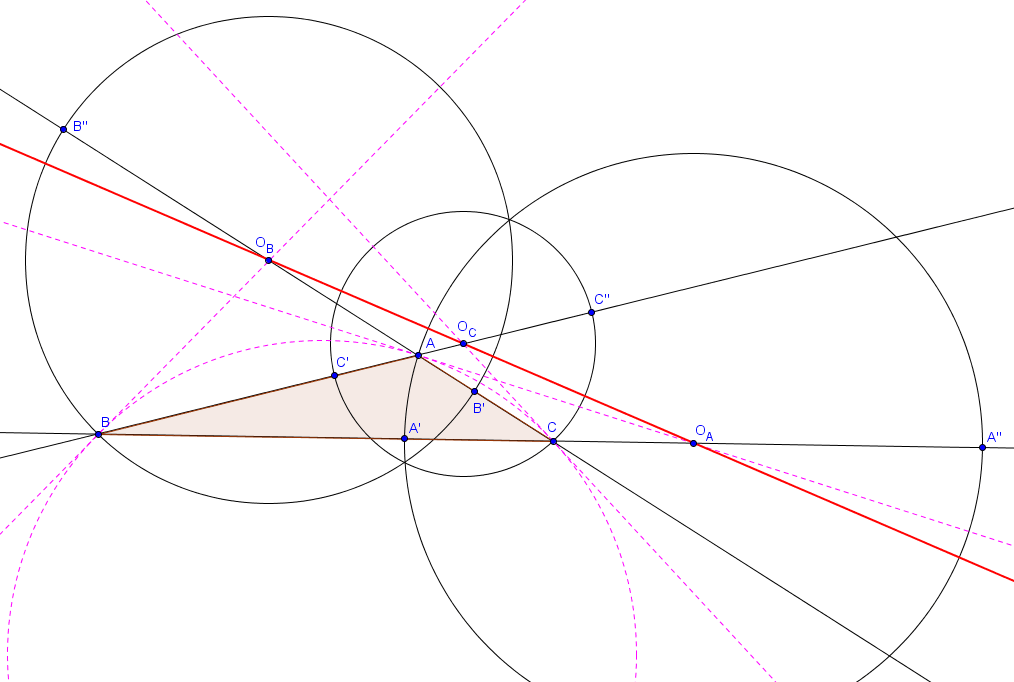
La droite de Lemoine porte le même nom que le point de Lemoine, que nous avons précédemment défini comme étant l'intersection des symédianes du triangle $ABC$. Cela n'est pas une coïncidence : en fait, la droite de Lemoine est la polaire du point de Lemoine par rapport au cercle circonscrit à $ABC$. (La définition de polaire est donnée dans ce chapitre).
Proposition (centre d'un cercle d'Apollonius)
Soit $ABC$ un triangle tel que $|AB| \neq |AC|$ et soit $\Gamma$ le cercle circonscrit à $ABC$. La tangente à $\Gamma$ en $A$ coupe la droite $BC$ en le centre du $A$-cercle d'Apollonius de $ABC$.
Démonstration
Notons $X$ l'intersection de la tangente à $\Gamma$ en $A$ avec la droite $BC$. On désire montrer que $X$ est le milieu de $[A'A'']$, où $A'$ est l'intersection de la bissectrice intérieure de $A$ avec $BC$ et $A''$ est l'intersection de la bissectrice extérieure de $A$ avec $BC$.

En utilisant l'égalité d'angles tangentiel et inscrit, on a
$$\widehat{XAA'} = \widehat{XAC} + \widehat{CAA'} = \widehat{ABC} + \widehat{A'AB} = 180^\circ - \widehat{AA'B} = \widehat{AA'C} = \widehat{AA'X}.$$ On en déduit que le triangle $AXA'$ est isocèle. Aussi, le triangle $AXA''$ est également isocèle puisque
$$\widehat{XA''A} = 90^\circ - \widehat{XA'A} = 90^\circ - \widehat{XAA'} = \widehat{XAA''}.$$ On a donc la suite d'égalités
$$|XA'| = |XA| = |XA''|,$$ ce qui signifie que $X$ est bien le milieu de $[A'A'']$ et donc le centre du $A$-cercle d'Apollonius.

En utilisant l'égalité d'angles tangentiel et inscrit, on a
$$\widehat{XAA'} = \widehat{XAC} + \widehat{CAA'} = \widehat{ABC} + \widehat{A'AB} = 180^\circ - \widehat{AA'B} = \widehat{AA'C} = \widehat{AA'X}.$$ On en déduit que le triangle $AXA'$ est isocèle. Aussi, le triangle $AXA''$ est également isocèle puisque
$$\widehat{XA''A} = 90^\circ - \widehat{XA'A} = 90^\circ - \widehat{XAA'} = \widehat{XAA''}.$$ On a donc la suite d'égalités
$$|XA'| = |XA| = |XA''|,$$ ce qui signifie que $X$ est bien le milieu de $[A'A'']$ et donc le centre du $A$-cercle d'Apollonius.
De la même façon, pourvu que $ABC$ n'est pas isocèle on peut construire le centre $O_B$ du $B$-cercle d'Apollonius et le centre $O_C$ du $C$-cercle d'Apollonius. Les trois centres sont alignés : cela découle du fait que les trois cercles ont exactement deux points communs. La droite de Lemoine est alors définie comme la droite passant par ces trois centres. Elle est représentée en rouge sur la figure suivante. Le cercle circonscrit au triangle $ABC$ ainsi que ses trois tangentes en $A$, $B$ et $C$ sont représenté en pointillés. Le triangle formé par ces trois tangentes est bien sûr le triangle tangentiel associé à $ABC$.

La droite de Lemoine porte le même nom que le point de Lemoine, que nous avons précédemment défini comme étant l'intersection des symédianes du triangle $ABC$. Cela n'est pas une coïncidence : en fait, la droite de Lemoine est la polaire du point de Lemoine par rapport au cercle circonscrit à $ABC$. (La définition de polaire est donnée dans ce chapitre).