Théorème d'Euler-Fermat
Indicatrice d'Euler
Définition
La fonction indicatrice d'Euler est définie pour $n \in \mathbb{N}_0$ par
$$\varphi(n) = \#\left\{ k \in \left\{1, 2, \ldots, n \right\} : (k, n) = 1\right\}$$ ou, autrement dit, $\varphi(n)$ est égal au nombre d'entiers entre $1$ et $n$ qui sont premiers avec $n$.
$$\varphi(n) = \#\left\{ k \in \left\{1, 2, \ldots, n \right\} : (k, n) = 1\right\}$$ ou, autrement dit, $\varphi(n)$ est égal au nombre d'entiers entre $1$ et $n$ qui sont premiers avec $n$.
Les premières valeurs de cette fonction sont données par le tableau suivant.
$$\begin{array}{c|c}
n & \varphi(n) \\[0.3em]
\hline
1 & 1 \\[0.3em]
2 & 1 \\[0.3em]
3 & 2\\[0.3em]
4 & 2\\[0.3em]
5 & 4\\[0.3em]
6 & 2\\[0.3em]
7 & 6
\end{array}$$ Par exemple, $\varphi(6) = 2$ car les seuls entiers entre $1$ et $6$ qui sont premiers avec $6$ sont $1$ et $5$.
Il ne semble a priori pas évident de calculer $\varphi(n)$ pour un $n$ quelconque, à part en regardant un par un les nombres entre $1$ et $n$. Il existe cependant une formule bien pratique permettant de calculer $\varphi(n)$ dès que l'on connait sa décomposition en facteurs premiers. Celle-ci se trouve en plusieurs étapes :
- Si $p$ est un nombre premier, alors $\varphi(p) = p-1$.
En effet, vu que $p$ est premier, tous les nombres entre $1$ et $p-1$ inclus sont premiers avec $p$. - Si $p$ est un nombre premier, alors $\varphi(p^m) = p^{m-1}(p-1)$.
Pour le comprendre, il suffit de se demander quels nombres entre $1$ et $p^m$ ne sont pas premiers avec $p^m$. Il s'agit des nombres ayant un facteur $p$, c'est-à-dire ceux qui sont divisibles par $p$. Ce sont donc simplement les entiers $p, 2p, 3p, \ldots, p^m$, qui sont au nombre de $p^{m-1}$. Le nombre d'entiers entre $1$ et $p^m$ qui sont premiers avec $p^m$ est dès lors égal à $p^m - p^{m-1} = p^{m-1}(p-1)$. - Si $a$ et $b$ sont premiers entre eux, alors $\varphi(ab) = \varphi(a)\cdot\varphi(b)$.
C'est le point le plus délicat à démontrer, et sa démonstration est donnée à titre informatif.
Il s'agit en fait d'une conséquence de théorème des restes chinois. Celui-ci nous dit en effet qu'il y a une correspondance entre les entiers de $\left\{1, 2, \ldots, ab\right\}$ et le produit cartésien $\left\{1, 2, \ldots, a\right\} \times \left\{1, 2, \ldots, b\right\}$. Elle consiste à associer au nombre $x$ le reste de sa division par $a$ et le reste de sa division par $b$ (en remplacant $0$ par $a$ ou $b$ mais cela a peu d'importance). Le théorème des restes chinois nous dit en fait qu'étant donnés les deux restes, il existe un unique $x$ duquel ils peuvent provenir. Or, on remarque que les nombres premiers avec $ab$ sont envoyés, par cette correspondance, exactement sur les couples $(y,z)$ où $y$ est premier avec $a$ et $z$ premier avec $b$. De là, il suit que $\varphi(ab) = \varphi(a)\cdot\varphi(b)$. - Si $n = p_1^{e_1} \cdot p_2^{e_2} \cdot \ldots \cdot p_k^{e_k}$, alors $\varphi(n) = p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)$.
Cela découle directement des deux points précédents, vu que chaque $p_i^{e_i}$ est premier avec les autres $p_j^{e_j}$.
Cette formule peut également se réécrire d'une forme parfois plus utile :
Formule (fonction indicatrice d'Euler)
$$\begin{align}
\varphi(n) &= p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)\\[0.5em]
&=n \cdot\left(1 - \frac{1}{p_1}\right)\cdot \ldots \cdot \left(1 - \frac{1}{p_k}\right)
\end{align}$$
\varphi(n) &= p_1^{e_1 - 1}(p_1 - 1) \cdot \ldots \cdot p_k^{e_k - 1}(p_k - 1)\\[0.5em]
&=n \cdot\left(1 - \frac{1}{p_1}\right)\cdot \ldots \cdot \left(1 - \frac{1}{p_k}\right)
\end{align}$$
D'un point de vue pratique, la première expression de cette formule nous indique que pour trouver $\varphi(n)$, il suffit de regarder la décomposition en facteurs premiers de $n$, et pour chaque facteur premier $p_i^{e_i}$ de remplacer un seul des $p_i$ par $p_i-1$.
Par exemple, pour $n = 3^3 \cdot 5^2$, on a $\varphi(n) = 3^2 \cdot 2 \cdot 5 \cdot 4$.
Les $100$ premières valeurs de $\varphi$ sont représentées sur le graphe suivant. Tous les points situés sur la diagonale correspondent aux nombres $n$ premiers, puisque ceux-ci donnent chacun $\varphi(n) = n-1$.
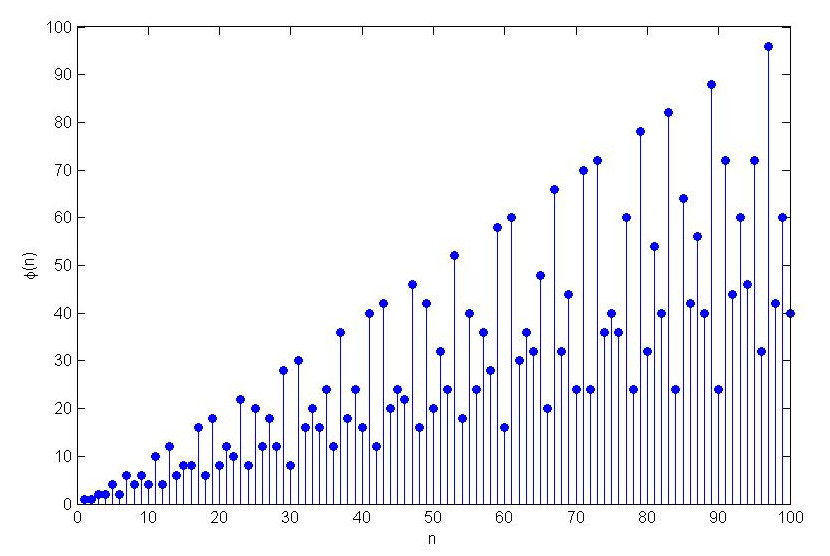
Premières valeurs de $\varphi$.